・正接の値は美しい 3類生 氏
正接(tan)は、正弦(sin)や余弦(cos)に比べてあまり目立たない。90°とか定義でき
ないし...。 そんな正接(tan)であるが、最近、「正接の値は美しい」ということを発見し
たので、報告したい。
正接(tan)の値、なんと、角度(単位は度)が、
7.5 22.5 37.5 52.5 67.5 82.5
のとき、きれいに求まるのだ!
正弦(sin)や余弦(cos)では、どうしても二重根号を使うことは避けられない。
(→ らすかるさんのHPの中のこちらを参照)
これに対して、正接(tan)の方はうまく打ち消しあって、美しい計算結果が得られる。
| θ | tan θ | ||
| 7.5° | −2+ |
= | ( |
| 37.5° | −2− |
= | ( |
| 52.5° | 2− |
= | ( |
| 82.5° | 2+ |
= | ( |
| 22.5° | |||
| 67.5° | |||
(求め方) 三角関数における次の公式を用いれば容易に求められる。
![]()
![]()
![]()
![]()
まず、tan 7.5°を求めてみよう。
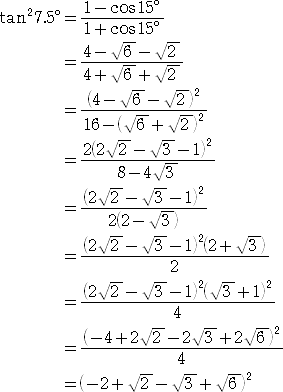
ここで、 (![]() +
+![]() )2−(2+
)2−(2+![]() )2 =1>0 より、
)2 =1>0 より、 ![]() +
+![]() > 2+
> 2+![]()
よって、 −2+![]() −
−![]() +
+![]() >0 なので、tan 7.5°= −2+
>0 なので、tan 7.5°= −2+![]() −
−![]() +
+![]()
である。 この右辺は因数分解できて、 tan 7.5°= (![]() −
−![]() )(
)(![]() −1)
−1)
でもある。(この形の方が、美しいかも...。)
上記の式変形では、 2+![]() =(
=(![]() +1)2/2 というところが急所である。これは、二重
+1)2/2 というところが急所である。これは、二重
根号の考えに似ている。
同様にして、tan 37.5°= (![]() −
−![]() )(
)(![]() +1) である。
+1) である。
これらの値が分かると残りの値は容易い。
tan 52.5°=1/tan 37.5°=1/(![]() −
−![]() )(
)(![]() +1)=(
+1)=(![]() +
+![]() )(
)(![]() −1)
−1)
tan 82.5°=1/tan 7.5°=1/(![]() −
−![]() )(
)(![]() −1)=(
−1)=(![]() +
+![]() )(
)(![]() +1)
+1)
また、
tan2 22.5°=(1−cos45°)/(1+cos45°)=(![]() −1)/(
−1)/(![]() +1)=(
+1)=(![]() −1)2
−1)2
![]() −1>0 なので、 tan 22.5°=
−1>0 なので、 tan 22.5°=![]() −1
−1
よって、 tan 67.5°=1/tan 22.5°=1/(![]() −1)=
−1)=![]() +1
+1
このような手法を用いれば、
tan 15°=2−![]() 、tan 75°=2+
、tan 75°=2+![]()
も簡単であろう。
(追記) 平成19年8月11日付け・・・塾長補足
上記で得られた tan 7.5°= −2+![]() −
−![]() +
+![]() という式から、 tan 7.5°が
という式から、 tan 7.5°が
4次方程式 x4+8x3+2x2−8x+1=0 の解になることが分かる。
このことに関連して、Anonymous さんが次のような問題を提起されている。
問1 tan 7.5°を解とする最小多項式 p(x)∈Q[x] を求めよ。
問2 商環 Q[x]/(p(x)Q[x]) は体となり、体 Q(tan 7.5°) と同型である。
このとき、 (tan 7.5°)7+(tan 7.5°)5+3 の逆元を求めよ。
問3 体 Q[x]/(p(x)Q[x]) は、Q の正規拡大体であることを示せ。
問4 Q(![]() )[x] において、p(x) を既約因子の積で表せ。
)[x] において、p(x) を既約因子の積で表せ。
問5 p(x) の零点は全て tanθi (i=1、2、3、4) の形に表される。 θi を求めよ。
この問題を解くために、「有限拡大体の性質」が少し参考になるだろう。
読者の皆さん、挑戦してみては如何でしょうか?
