・日常生活のMKS S.H 氏
日常生活を営む上で、知っていると便利な基本的定数がある。そういうものをまとめてみ
た。
〇 車で10分=自転車で25分=徒歩で75分
車は、時速30km、自転車は時速12km、徒歩は、時速4km
○ 車移動の所要時間 高速道路は、時速80km 一般道は、時速30km
車移動の際の所要時間の見積もりとして、上記で計算するとだいたいの目安となる。
○ 不動産屋さんの徒歩1分=分速80m
○ 100g=Sサイズの卵2個分
○ お札の幅 千円札は15cm、1万円札は16cm
○ 1円玉の直径は2cm、重さは1g
5円玉の重さは1匁(3.75g)
○ はがき 横は100mm、縦は148mm
次の覚え方が有名である。 → 横井まるまる立て石屋
自己流に覚え方を考えてみた。 → 止まれ、従者
○ グラスの半分量を見いだす方法
今、ビールジョッキに満杯にビールが注がれている。ビールの泡はないものとする。量りを
用いないで、量を丁度半分にすることを考える。

そのためには、水面の端点がジョッキの内面の底に丁度ついたときに、量が丁度半分に
なる。

直感的には明らかだろうが、計算でも次のように示される。
ジョッキの底面は、半径 r の円とし、ジョッキの高さを h とおく。
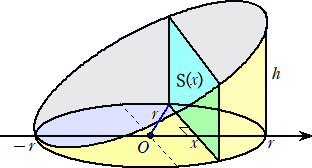
上図において、切り口の面積S(x)は、
S(x)=2√(r2−x2)・(x+r)(h/(2r))=(h/r)(x+r)√(r2−x2)
よって、体積Vは、
V=(h/r)∫-rr (x+r)√(r2−x2)dx
=(h/r)∫-rr x√(r2−x2)dx+h∫-rr √(r2−x2)dx
ここで、x√(r2−x2)は奇関数なので、 ∫-rr x√(r2−x2)dx=0
また、 ∫-rr √(r2−x2)dx=πr2/2 なので、 V=πr2h/2
ところで、半径 r の底円で、高さ h の直円柱の体積は、πr2h なので、
上記立体の体積Vは、直円柱の体積の丁度半分になっている。
○ ラーメン丼一杯のスープ=350mlの缶ジュース=ビールの小瓶
○ TV視聴率1%=114万人 ・・・ 調査方法によって種々あり、一概には言えない。
(計算式) 5852万世帯×2.18人/世帯×0.9×0.01
○ 人間の歩幅=目の高さの半分
普通の歩幅は、(身長)×37%位 のところ、「大股」で歩くとは、(身長)×45%位
例 身長が180cmの場合、普通の歩幅は、67cm位で、「大股」で歩く場合は、81cm位。
横断歩道の白い線の幅が45cmなので、それを踏まずに越えられれば、歩幅は、67cm
位になる。
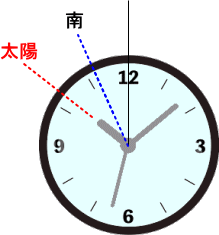
○ 腕時計で方角を知る方法(ただし、晴天の日中限定)
腕時計を水平にして、短針を太陽に合わせる。そのとき、12時と短針の間を2等分した方
向が南となる。
○ 大さじ1/2の量り方 ・・・ 高さがほぼ7割くらい
何とはなしにTVで料理番組を見ていたら、「大さじ1/2」の量り方が話題になっていた。結
論から言うと、「高さがほぼ7割くらい」が目安だそうだ。
「大さじ1」は、15mlで、表面張力で目一杯に盛り上がった状態を示す。因みに、「小さじ1」
は、5mlで、「大さじ1=小さじ3」という関係が成り立つ。「大さじ1=小さじ4」という関係だっ
たら、「大さじ1/2」は「小さじ2」なわけで、無問題なのだが、なぜか、「大さじ1=小さじ3」だ
という。数学の世界の「素数」のような感覚で、料理の世界は奥深い。
液体ではなく固体だったら、すり切りにしたあと、上から半円になるようにヘラを垂直に入
れれば易しいのだが、液体の場合に「高さが7割くらい」というのは実は悩ましい。
「大さじ1/2」が「高さがほぼ7割くらい」であることを計算してみた。
半径 r の半球の表面から高さ a に水面がある液体の体積を求める。半球の体積は、
2πr3/3であることに注意する。

上図の体積Vは、
V=π∫-r-a (r2−z2)dz=π(−r2a+a3/3+2r3/3) で与えられる。
題意より、 π(−r2a+a3/3+2r3/3)=πr3/3 なので、 a3−3r2a+r3=0
ここで、 0≦a≦r で、 F(a)=a3−3r2a+r3 とおき、関数のグラフの変化を調べる。
F’(a)=3a2−3r2=0 とおくと、 a=r で、 0≦a≦r において、 F’(a)≦0 から
F(a)は単調減少である。F(0)=r3>0 かつ F(r)=−r3<0 から、中間値の定理より、
F(a)=0 は、0 と r の間にただ一つの解を持つ。
ここで、 F(r/3)=r3/27>0、F(r/2)=−3r3/8<0 なので、F(a)=0 は、r/3 と r/2
の間にただ一つの解を持つことが分かる。
以上から、水面から1/3強ほどのところに、「大さじ1/2」が存在するらしい。
〇 紙のサイズでは、A版、B版の2種類が流通している。(→ 参考:「紙のサイズ」)
A版、B版のおおもとは、それぞれA0版、B0版で、そのサイズは、
A0版: 841mm×1189mm 面積 1m2
B0版:1030mm×1456mm 面積 1.5m2
と決められている。
これらをもとに、順次半分に折ることにより、A1、A2、・・・、B1、B2、・・・ が得られる。
したがって、B4の大きさは、A4の1.5倍で、A4の3枚分がB4の2枚分に相当する。
次の事実は、実際の生活で活用できるマメ知識かもしれない。
A4の用紙の長辺の中点は、B5の長辺の端点の一方をA4の頂点に合わせて見い
だせる。
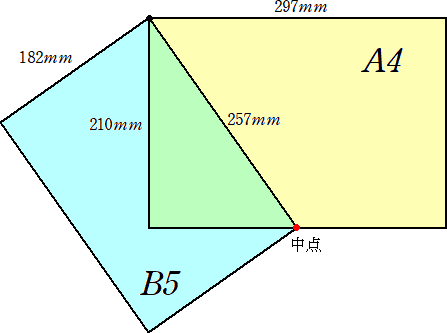
実際に、A4のサイズは、210×297 、B5のサイズは、182×257 で、
210^2+(297/2)^2=66152.25
から、その平方根は、だいたい 257.200 くらいとなる。
この長さは、B5の長辺の長さに等しい。
今までは、A4を2分割するとき、軽く折って折り目をつけていたのだが、このようにすれば
折り目を付けずにエレガントに2分割の目安をつけることが出来る。
○ 街中で旧友に出会って、「いや〜、○○年ぶりだねェ〜」ということはよくあること。この
「○○ぶり」という言い方は、満の数え方で、起点は「0扱い」になる。
例 令和元年に初優勝し、令和4年に再び優勝した場合、「3年ぶり2回目の優勝」となる。
計算式は、 4−1=3 である。
例 今月の8日に出会って、また同じ月の21日に再会した場合は、「13日ぶりの再会」と
なる。計算式は、 21−8=13 である。
これに対して、○○年目とか、○○回目という言い方がある。この言い方は、数えの数え方
で、起点は「1扱い」となる。
例 新入社員は、入社1年目
同じような言い方に、○○周年という言い方もある。これは、起点が「0扱い」で、満の数え方
をする。物事が始まってどれくらいの年数が経ったのかを知るときに使われる。
例 8月28日の次の年の8月28日で、1周年となる。
勤続年数も満の数え方をする。
例 4月1日入社の場合、5月21日で、勤続年数は、0年1ケ月となる。
このように、日常生活を送る上で、「数え」で数える場合と「満」で数える場合の2通りがある。
最近、「数え年」というものを意識する機会があった。「数え年」は生まれた時を「1歳」とする
年齢の数え方である。私には生後すぐに亡くなった妹がいるのだが、墓誌を見ると、「一歳」
と記されている。日本では古来年齢は「数え年」だったのだ。
「数え年」には「0」という概念がなく、数え始めの年が1となる。だから、21世紀の始まりも
2000年ではなく、2001年なわけだ。
例 地下3階から地上4階まで階段を上るとき、何階分駆け上がるだろうか?
計算式は、 4−(−3)−1=6 で、6階分を駆け上がる。「0階」はないので、1を減じ
る必要があるわけだ。
○ 水が凍ると体積は1/11増えるので、ペットボトルを満杯にして冷凍庫で凍らせるのは
危険であるが、最近は、凍らせてもOKというペットボトルも販売されている。冷凍効率
を上げるために積極的に冷凍庫にペットボトルを置いている家庭も多いに違いない。
そこで、問題です。氷が水になるとき、体積はどれだけ減るだろうか?
答えは、1/12だけ減る。減る割合が、増える割合よりも少ないんですね!
実際に、氷Vが溶けて、水Wになったとき、 V=(12/11)W という関係式が成り立つ。
よって、 W=(11/12)V から、1/12だけ減る。
〇 今日残っている時間は、すでに経過した時間の7/9である。現在の時刻は?
24÷(1+7/9)=13.5 から、今、13時30分である。
○ 歩く速さは健康のバロメーターと言われる。
分速96mだと、平均寿命が30年以上あるらしい。ちょっとゆっくり目の分速48mだでも
平均寿命は15年ほどになるらしい。皆さんの歩く速さは如何?
○ マイナンバーカードを保険証代わりにというキャンペーンが行われているが、なかなか
マイナンバーカードの普及が進まないし、マイナンバーカードを保険証として取り扱う医
療機関の数も拡がらない。
そのなかなか拡がらないネックの一つが、電子的保健医療情報活用加算というもの。
令和4年8月時点で、初診は7点、再診は4点、薬局は3点と決められている。
(医療費診療報酬の1点=10円)
例えば、初診でマイナンバーカードを保険証に使った場合、自己負担割合3割として、
7(点)×10(円)×0.3(負担割合)=21(円)
が加算されるということ。通常の保険証利用だと、9円 なので、マイナンバーカード利用の
場合は、12円も負担が増えることになる。
政府は、負担割合を10月に、次のように変更することを考えているらしい。
マイナンバーカード利用の場合 初診 2点(現状の案より、5点減)
従来の保険証利用の場合 初診 4点(現状より、1点増)
このような変更で、マイナンバーカードの普及は進むのだろうか?
○ 数の大きさを把握するときに、目安があると分かりやすい。
例えば、「123456789円」と書かれるよりも、「123,456,789円」と書かれてある方
が分かりやすいし、「1億2345万6789円」と書かれると、数の大きさの実態がひしひしと
伝わってくる。
私がパソコンをいじり始めた頃は「キロ」が主要単位であったが、それがいつの頃からか
「メガ」に取って代わり、最近では「ギガ」が日常生活でも普通に使われるようになった。
大きい数、小さい数の単位をまとめておく。
| 倍率 |
読み方 |
単位 |
|
倍率 |
読み方 |
単位 |
| 10 |
デカ |
da |
|
10^(-1) |
デシ |
d |
| 10^2 |
ヘクト |
H |
|
10^(-2) |
センチ |
c |
| 10^3 |
キロ |
K |
|
10^(-3) |
ミリ |
m |
| 10^6 |
メガ |
M |
|
10^(-6) |
マイクロ |
μ |
| 10^9 |
ギガ |
G |
|
10^(-9) |
ナノ |
n |
| 10^12 |
テラ |
T |
|
10^(-12) |
ピコ |
p |
| 10^15 |
ペタ |
P |
|
10^(-15) |
フェムト |
f |
| 10^18 |
エクサ |
E |
|
10^(-18) |
アト |
a |
| 10^21 |
ゼタ |
Z |
|
10^(-21) |
ゼプト |
z |
| 10^24 |
ヨタ |
Y |
|
10^(-24) |
ヨクト |
y |
| 10^27 |
ロナ |
R |
|
10^(-27) |
ロント |
r |
| 10^30 |
クエタ |
Q |
|
10^(-30) |
クエクト |
q |
ロナ、クエタ、ロント、クエストの4つが国際度量衡総会(2022.11.18)で追加された。ヨタが
制定された1991年以来、31年ぶりの追加となった。また、コンピュータシステムに影響があ
るとして、「うるう秒」が2035年までに廃止されることも採択された。
この単位を用いれば、数字の区切り「,」の代わりに、
「123,456,789円」 → 「123M456K789円」
とも書かれる。4Kテレビの「K」は、まさに「1000」という意味で、画面の解像度を表す。
○ 1日に摂る必要がある水分量は、次の式で求められる。
(体重)×30ml
例 体重が100kgの場合、必要な水分量は、「3リットル」となる。牛乳3本分と考えれば、
軽くいけるかも...。
〇 血液型のルーツ
A型 ・・・ 農耕民族
B型 ・・・ 遊牧民族
O型 ・・・ 狩猟民族
AB型 ・・・ 農耕民族+遊牧民族
○ 運転免許証の12桁の意味
| 1 2 |
3 4 |
5 6 7 8 9 10 |
11 |
12 |
初めて
交付を
受けた
都道府
県番号 |
初めて
交付を
受けた
西暦の
下2桁 |
公安委員会の
管理番号 |
チェック
デジット |
再交付
回数 |
○アイスコーヒーにするかホットコーヒーにするかの目安は、気温が19℃
○日本とベトナムの時間差は、2時間
ベトナム現地時間で朝の9時は、日本時間で、朝の11時
ベトナム〜日本の飛行時間は、6時間かかるので、
日本を朝の9時に出発すれば、日本時間でベトナムに昼の3時に到着する。
これは、現地時間で、昼の1時に相当する。
ベトナムを朝の9時に出発すれば、日本には、ベトナム時間で昼の3時に到着する。
これは、日本時間で、夕方の5時に相当する。
偏西風の影響で、日本→ベトナム間の飛行時間よりも、ベトナム→日本間の飛行時間の
方が短い。ということは、先の例で、夕方の5時より前に日本に着くということかな?
○「常温」というと、15℃〜25℃ぐらいかなと思っていたが、JISでは明確に 20±15℃
と定められている。5℃〜35℃と、常温の範囲は幅広いんですね。でも、35℃が常温と
言われてもアンビリーバブルです...。
○「1万円札」の現価は、25円程度と言われる。
○2000(平成12)年4月から始まった介護保険制度。介護を社会全体で支えるということ
で、40歳以上は保険料を納めなければならないわけだが、その負担がかなり大変である。
いつかはお世話になるものなので、保険料を納めてはいるものの、実際にその介護サー
ビスを受ける際にも、「自己負担」が1割かかり、全くの無料というわけでもないという、何
か理不尽な制度である。
介護保険で、必要な介護サービスの提供や介護用品の貸与など現物給付が受けられる。
これらに関与する方がケアマネージャーと言われる。
介護サービスを受けるまでのプロセス
(1) 地域包括センターや自治体の窓口で申請
(2) ケアマネージャーの決定
(3) 介護認定審査会で審査(30日以内)
審査項目
・身体機能、起居動作 ・生活機能 ・認知機能 ・精神、行動障害 ・社会生活への適応
・特別な医療の有無
審査の結果、要支援1〜2、要介護1〜5 と認定される。
要支援1では自己負担額が5千円程度だが、要介護5では、自己負担額が3万6千円ほど
になる。
利用限度額の範囲内で、ケアマネージャーが必要な介護サービスを組み立てることになる。
○新幹線座席のコンセントについて AC100V、2A、60Hz の規格であるらしい。
スマホの充電器やノートPCのACアダプターに対応する。
○「京」は「兆」の次に大きな大きさを表す単位である。クジラは、魚へんに京と書いて「鯨」
で表されるが、哺乳類なのに、魚へんというのは面白い。相当の昔、クジラは魚と思われ
ていたのだろう。身体が大きいという意味で、「京」の字があてられたのかな?
○10円玉には、銅が95%、亜鉛が3〜4%含まれ、青銅と言われる。5円玉には、銅が
60%〜70%、亜鉛が30%〜40%含まれ、黄銅と言われる。
○液体が酸性かアルカリ性かを表す尺度に水素イオン指数(pH)がある。以前は、「ペーハ
ー」とドイツ語読みであったが、最近は、「ピーエッチ」と呼ぶらしい。
純水のpH7に対して、雨水はpH6、海水はpH8。海水がアルカリ性とは意外でした。酢の
pHは3、レモン果汁はpH2に対して、胃液のpHは1とかなり酸性度が高いんですね!
○海上交通で、「面舵いっぱい」とか「取り舵いっぱい」という用語は、干支が由来である。
すなわち、
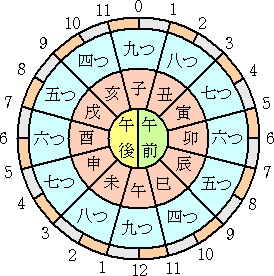
「面舵」・・・進行方向右(卯の方角)に舵をきる
「取り舵」・・・進行方向左(酉の方角)に舵をきる
海上で、船同士の正面衝突を避けるルールが、「両方の船が面舵いっぱい」である。
このルールは、人混みで歩く時にも適用してほしいものだ。一番困るのは、ときどき、右に
行こうか、左に行こうか迷う方がいて、そのため、互いがその地点で立ち止まってしまうこと
がある。
「面舵いっぱい」のルールが歩く人全員に周知されれば、道の途中で立ち止まることなく
人とすれ違うことが出来るだろう。
○「アーバンベア」という言葉が出来るくらい、最近人里まで熊が出没している。以前は、熊
と人間は微妙に住み分けをしていて、人の住む界隈に熊が出没することは稀であった。
しかも熊は人間に対して怖れを抱いていて、臆病な性格から、熊の方が速攻で逃げるとい
うことが多かったように思う。しかし、最近の熊は、人間慣れしてきたせいか、怖れを抱くこと
もなく出会っても平然としている。人間の食するものの味を覚えると、それに執着して、同じ
場所に出現するのだという。
不意に熊と出会った場合に決してやってはいけない事は、熊に背中を見せることだという。
熊と対面しながら、後ずさりし、逃げるのが大切らしい。また、大きな音を立てると、熊が驚
いて熊の方から逃げるとも言われる。
熊は意外にも足が速い。時速48kmくらいあるらしい。ヒグマだと時速56kmとも言われる。
人類最速の男ウサイン・ボルトは、100mを9秒58で走るので、時速に換算すると、37.6
kmとなり、熊よりも遅い。ということは、一般の人が熊から走って逃げ切ることは、ほぼ不可
能ということだ。
チータは、100mを3.72秒で走るので、時速に換算すると、110kmとなる。ウサイン・ボ
ルトの約3倍の速さである。チータなら楽勝で熊から逃げられるかな?
○大谷翔平選手が、10年総額7億ドルという契約で、エンゼルスと同じくロサンゼルスの球
団ドジャースに移籍する。日本円に換算して、1015億円という金額に度肝を抜かれた。
これまでのスポーツ選手の契約金としては史上最高額とのことである。
金額があまりに大きいので、実感するために、いろいろ計算してみた。
1万円札は、横16cm、縦7.6cm、厚さ0.1mm、1g/枚 である。
そこで、百万円の札束1つは、1cm、100g となり、1億円だと、1m、10kg である。
そうすると、1015億円ということは、厚さにして、1015m=1.015km もあり、重さでは
10150kg=10.15トン となる。とても一人で持てる量ではない。
1万円札1枚の面積は、0.01216m2 であるので、1億円だと、121.6m2 となり、
1015億円を床に敷き詰めれば、 123424m2=0.123424km2 となる。
よく比較に使われる東京ドームの広さは、46755m2 なので、1015億円は、東京ドーム
2.64個分に相当する。この広さは、東京ディズニーランド(0.52km2)の約1/4でもある。
吉野家の特盛牛丼は、1杯820円(税込)である。大谷選手の契約金で、この牛丼を何杯
食べられるか計算してみた。もっとも大谷選手は、ほとんど外食をしないらしいが...。
101,500,000,000÷820=123,780,487.8(杯)
1日3食すべて牛丼と仮定すると、食べ尽くすのに、 11万3千年くらいかかるようだ。とて
も生きているうちに食べ尽くすことは困難ですね!
○第100回箱根駅伝は、青山学院大学が2年ぶりに総合優勝を飾った。
往路5区間107.5kmを5時間18分13秒、復路5区間109.6kmを5時間23分12秒で
駆け抜けた。
ところで、時速km/hを秒速m/sに換算するには、
1km/h=1000m/3600s=1/3.6(m/s)
なので、青山学院大学の選手の速さは、時速で、
217.1÷10.69027・・・=20.30817202・・・ (km/h)
となるから、秒速では、
20.30817202・・・÷3.6=5.641158894・・・ (m/s)
となる。この速さは、100m走に換算すると、 17.72685398・・・秒 となる。
100mに限定すれば、このタイムはそれほど速いとは感じられないかもしれないが、この
速さを10時間41分25秒の間継続するわけで、その大変さがヒシヒシと伝わってくる。
○令和6年10月に郵便料金の値上げが予定されている。
定型封書は、84円(25g以下)、94円(50g以下) → 重量による区別はなしで、110円
ハガキは、63円 → 85円
封書は1994年以来30年ぶりの値上げ、ハガキは7年ぶりの値上げとなる。
○スーパーでは、よく「まとめ売り」が行われる。1個当たりの値段を計算するのは、消費者の
性(さが)かな。
普段はあまり電卓を持ち歩かないから、適当に概算で比較する人も多い。今、スマホ持ち
が多いので、スマホの電卓機能でサクッと計算する方もいらっしゃるだろう。
電卓なしで比較が出来れば理想なのだが、次の問題を考えてみよう。
問題 6個で460円の商品Aと8個で610円の商品Bがある。商品単価が安いのは、A、B
のどちらだろうか。
電卓があれば、 460÷6=76.66・・・、610÷8=76.25 から、商品Bの方が単価
は安いことが分かるが、暗算で、その計算をやるのは少ししんどい。
(解) 6と8の最小公倍数は24なので、
商品A : 460×4=1840(円) 商品B : 610×3=1830(円)
から、商品Aよりも商品Bの方が単価は安い。 (終)
(コメント) 多分、掛け算の方が、暗算は容易だろう。
○ 電源ONは「1」、電源OFFは「0」 で、電源ONが「−」であるのは誤り。
○ 令和6年夏(8月〜9月)は、「令和の米騒動」と言われる。今、全国で米が買えずに困っ
ている方が多い。「平成の米騒動」は、平成6年。同僚に農家の方がいて、米不足に困った
様子もなく、とてもうらましく思ったことを覚えている。我が家がタイ米を初めて食べた年でも
ある。カリフォルニア米というのもあった。タイ米は、当初はそこそこの値段で売られていた
が、最後は、景品として無料で配られていたような記憶がある。タイ米は細長くて、カレーに
最も合う米だと思った。
農水省は、新米が流通するようになれば米不足は落ち着く、米の価格が下がるのは困る
という理由で、備蓄米の放出を渋っているが、物価の高止まりをなぜ政府は解消しようとし
ないのか、消費者目線では不可思議だ。農家目線では、米の値段が下がるのは困るという
のは理解できるが、ガソリン税のような政府からの支援というのはないのだろうか?
米1合は150gで、炊飯すると345gに増え、お茶碗2杯分である。米不足で人気のレトル
トパックのご飯は、何故か180gが基本である。パスタ100gは、茹でると250g相当になり、
うどん、そば100gは、茹でると300g相当に膨れる。
米1袋は、5kgが基本である。以前は、10kgの袋で売られていたが、最近は、なぜか見
ない。単純計算で、米5kgは、約33合分あり、お茶碗に換算して、約66杯分である。
米5kgは、3000円ほどなので、お茶碗1杯分は、およそ46円となる。以前は、米5kgが、
2000円ほどで売られていたので、現在は、5割増に高騰している。お茶碗1杯分は、およ
そ31円であったので、気持ちよく腹一杯に食べられたのだが、それも出来にくくなった。
1合は180mlで、米粒に換算すると、6483粒である。よって、お茶碗1杯には、3247粒
の米粒が入っていることになる。
○MLBの試合中継を見ていると、試合開始時間が日本時間で考えると、とんでもないことに
なっている。そこで、東京・ソウルを基準に、世界の主な都市の時差をまとめてみた。アメリカ
には、一つの国の東西で、5時間ぐらいの時差があるんですね!
| 東京、ソウル |
0 |
2日午前11時 |
| 北京、香港、シンガポール |
−1時間 |
2日午前10時 |
| バンコク、ジャカルタ |
−2時間 |
2日午前9時 |
| ダッカ |
−3時間 |
2日午前8時 |
| カラチ |
−4時間 |
2日午前7時 |
| ドバイ |
−5時間 |
2日午前6時 |
| バグダッド |
−6時間 |
2日午前5時 |
| カイロ、アテネ |
−7時間 |
2日午前4時 |
| パリ、ローマ、ベルリン |
−8時間 |
2日午前3時 |
| ロンドン |
−9時間 |
2日午前2時 |
| リオデジャネイロ |
−12時間 |
1日午後11時 |
| ニューヨーク、モントリオール |
−14時間 |
1日午後9時 |
| シカゴ、メキシコシティ |
−15時間 |
1日午後8時 |
| ロサンゼルス、シアトル |
−17時間 |
1日午後6時 |
| アンカレッジ |
−18時間 |
1日午後5時 |
| ホノルル |
−19時間 |
1日午後4時 |
| シドニー、グアム |
+1時間 |
2日午後0時 |
| ウェリントン |
+3時間 |
2日午後2時 |
○「1割引」と「1割増」、どちらがお得なのかを計算してみた。
100g 100円の商品の「1割引」は、100g 90円 すなわち、1g当たり 0.9円になると
いうことである。
それに対して、
100g 100円の商品の「1割増」は、110g 100円 すなわち、1g当たり 0.909円に
なるということである。
「1割引」の方が、「1割増」よりお得になるのかな...。
割引率を変えても、割引してもらった方がお得です!
(追記) 当HPがいつもお世話になっているHN「kuiperbelt」さんから話題(1)(2)をご提供い
ただきました。(令和6年12月22日付け)
(1) 建物の階数の数え方ですが、日本、米国、中国では地上階は1階ですが、欧州では、
例えば、英国では、ground floor、ドイツでは、Erdgeschoss といって、日本、米国、中国でい
う 2 階、3 階は、英国では、1st floor、2nd floor、ドイツでは、1.Obergeschoss、2.Obergeschoss
となっていて、エレベーターのボタン表示も 0、1、2、・・・ となっています。なお、地下階の
表示は、-1、-2、・・・ でした。
(2) 113番元素はニホニウムですが、ニホニウムという名前が決まるまでは、IUPAC(国際
純正・応用化学連合)が定めた仮の名称でウンウントリウムとよばれていました。IUPACの
規則では、
0 nil ニル 、1 un ウン 、2 bi ビ 、3 tri トリ 、4 quad クアド 、5 pent ペント 、
6 hex ヘキス 、7 sept セプト 、8 oct オクト 、9 enn エン
で原子番号の各桁を表し、接尾辞の「-ium」をつけるので、113番元素は、
「1=ウン、1=ウン、3=トリ」+「-ium」
で、ウンウントリウムとなります。未発見の119番、120番の元素はウンウンエンニウム、ウン
ビニリウムとなります。
ウンウントリウムは非公式にはエカタリウムともいわれていましたが、エカはサンスクリット語
で1を意味し、周期律表でタリウムの1つ下にある元素という意味になります。メンデレーエフが
未発見元素を予言したとき、現在のガリウム、ゲルマニウムをエカアルミニウム、エカケイ素と
称していました。現在のレニウムはドヴィマンガンと称していましたが、ドヴィはサンスクリット語
で2を意味し、周期律表でマンガンの2つ下にある元素という意味になります。
なお、エカマンガンは、テクネチウムですが、安定同位体が存在しない元素となります。
〇 以前、昭和の元号に「25」を足すと、西暦の下2桁を表したが、令和の時代になって、
昭和も遠くになりにけり。
2025年は、丁度、昭和100年であり、平成37年であり、令和7年でもある。したがって、
令和の元号に「18」を足すと、丁度、西暦の下2桁を表す。この「18」は、「018」と考えれ
ば、語呂合わせで「れ(0)い(1)わ(8)」と覚えれば、覚えやすい。
〇 今まで気にもとめていなかったが、JRの紙の切符をよく見ると、「乗車券」の下に
□□□□・・・・・・・・
という謎の記号が印字されている。これは、何だろう?
「東京〜熱海間」「米原〜新大阪間」「新下関〜博多間」という3つの区間のどこを経由する
のかを示す記号らしい。在来線は、□□□□であるが、新幹線は、■■■■となるようだ。
例 東京〜小田原間の在来線の切符には、「□□□□・・・・・・・・」と印字される。
例 東京〜新大阪間の在来線の切符には、「□□□□□□□□・・・・」と印字される。
例 東京〜新大阪間の新幹線の切符には、「■■■■■■■■・・・・」と印字される。
3つの区間の何れも含まない場合は、「 」と印字される。
例 静岡〜浜松間の在来線の切符には、「 」と印字される。
チケットレス乗車が普及してきていて、紙の切符を見る機会もだいぶ減ってきているが、
何とはなしに紙の切符を眺めて見るのもいいものだ。
○ 電子レンジで加熱調理をすることは、日常生活の基本的な必須アイテムだろう。
私の2番目の姉は、永らく電子レンジもない、炊飯器もない生活を送っていたが、ご飯も鍋
で美味しく炊けて、不便さは感じなかった。
コンビニなどで出来合いのお弁当を買うと、「500wで3分」とか、調理時間が書かれている。
手持ちの電子レンジは、600wで、適当に時間を縮めて温めることが多かった。最近の電子
レンジは、温めの温度を設定すると、自動で温めてくれる。しかも、温め終わると、電気料の
目安も表示してくれる。便利な世の中になったものだ。
温度設定で「レンチン」する最新式の電子レンジは別にして、まだまだ500w、600w、1000w
の設定で、何分加熱という電子レンジも多い。
その際に用いる変換式は、 発熱量(ジュール)=ワット数(ワット)×時間(秒) である。
例 「500wで3分」の場合、600wで加熱する時間は何分か?
500×180÷600=150 より、2分30秒加熱すればよい。
○ 将棋の王将戦第2局が令和7年1月25・26日に京都・伏見稲荷大社で行われ、先手の
藤井聡太竜王・名人が挑戦者の永瀬拓矢九段に勝利した。これで、藤井聡太竜王・名人は、
先手番勝利が32連勝になるという。
一般に、将棋の先手番勝利の確率は 0.54 と言われているので、32連勝する確率は、
(0.54)32=0.00000000273・・・=2.73×10-9 となる。
10億回のうち、ほぼ2〜3回起こる程度で、藤井聡太竜王・名人の偉業に驚かされる。
〇 首都圏の鉄道では、東海道線、横須賀線、常磐線、宇都宮線、高崎線などで普通車に
グリーン車が連結されている。2025年3月15日からは、中央線でもグリーン車のサービ
スが開始された。
最近、東海道線の沿線の火災により、グリーン車が激混みのときがあった。デッキまで人
が溢れ、全く座ることが出来なかった。デッキでもグリーン券は必要ということで諦めていた
が、次のようなグリーン料金の払い戻しの制度があることを最近知った。
車掌さんに「着席出来ないので、普通車に移動します」と申告すれば、払い戻しのための
証明書を発行してくれるらしい。1年間有効なので、みどりの窓口などで、手数料なしで払い
戻してくれる。
これは是非知っておくと役立つ情報だ。
○ バウムクーヘンは、バウム(木)とクーヘン(ケーキ)から分かるように、ドイツ語である。
日本では、扇形に切り分けるのが一般的であるが、本場ドイツでは、「削ぎ切り」される。
滑らかな口当たりになり、食感が変わるそうだ。今度、試してみよう!
○ 日本時間で、10月1日からMLBでワイルドカードシリーズが始まった。(2025年度)
ナ・リーグ西地区1位のドジャースは中地区2位のレッズと対戦し、大谷翔平は初回と6回
にHRを打ち勝利に貢献した。先発のスネルも7回まで好投したが、その後の中継ぎがよ
くなかった。ベシアとエンリケスが投げたのだが、ベシアの防御率は何と「54.0」という凄
い数字をたたき出した。防御率とは、1試合で取られうる得点を指す。ベシアは1アウトを
とって2失点なので、防御率は、 2×3×9=54 と計算される。ドジャースは、レッズに
2連勝し、フィリーズとの地区シリーズに進出した。
以下、工事中!








