次の２等辺三角形

　　　

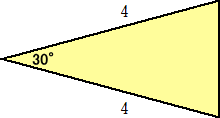
の面積を求めよと問われたら、多分いくつかの解法が考えられる。

（１）　三角形の面積の公式から、　Ｓ＝（１/２）・４・４・ｓｉｎ３０°＝４

（２）　頂点から対辺に垂線を下ろして、下図を得る。

　　　

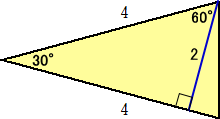
　　求める面積は、　Ｓ＝（１/２）・４・２＝４

＃この解法だと、中学生でも十分対応可能だろう。（→　参考：「面積計算１２」）

（３）　（１）（２）とは異なる第３の解法を最近知ることができた。

　　　３点を通る外接円が存在するので、下図を得る。

　　　

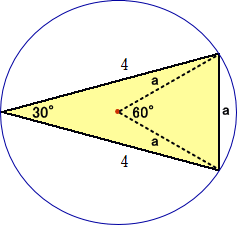
　　上図において、三平方の定理より、

　　　　（ａ＋ａ/２）²＋（ａ/２）²＝４²

　　これより、　ａ²＝１６（２−）　から、　ａ＝２（−１）

　　求める三角形の面積は、　（２＋）ａ/２・ａ/２＝（２＋）ａ²/４＝４


（コメント）　（３）の外接円を意識する解法は、他の問題についても有効である。

　例えば、次の２等辺三角形の面積を求めてみよう。

　　　　　　

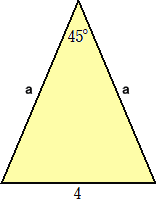
　これについても外接円を描いて、

　　　

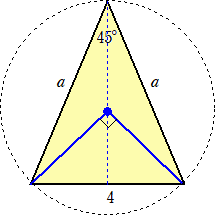
　三角形の高さは、　２＋２　であるので、求める三角形の面積は、

　　　４×（２＋２）÷２＝４（１＋）


（コメント）　もちろん、余弦定理を用いてもよい。

　　４²＝ａ²＋ａ²−２ａ²・ｃｏｓ４５°より、　ａ²＝１６/（２−）＝８（２＋）

　よって、求める面積は、　Ｓ＝（１/２）ａ²・ｓｉｎ４５°＝４（２＋）/＝４（１＋）


　また、次のような別解も知られている。

　問題の２等辺三角形は、下図のような、１辺の長さが４の正８角形の一部分である。

　　　

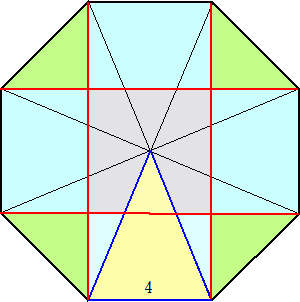
　正８角形の面積は、

　（２）²/２・４＋４・（２）・４＋４²＝３２（１＋）

なので、求める三角形の面積は、　３２（１＋）÷８＝４（１＋）