現在、東京オリンピック2020で連日熱戦が行われている。この中の種目でのバスケットボ
ールとサッカー競技について考えてみる。

　瞬時に配置が変化しながらボールをパスしてゴールを目指すことを行うわけであるが、2人
の間に敵が位置すれば、この２人は直接ボールをやりとりすることは難しく、第３者を介して
繋ぐことを、その戦術として常に行っている。

　そこで、どの選手も他の仲間のどの選手へにもパスを繋げられるルートがどれほど存在で
きるかを、次のようなモデルにして考えてみることにする。

　今円周上に、ｎ人が位置しており（トポロジー的には変わらないので、等間隔で位置してい
るとする。）、このｎ人同士は直線を辿れば、どの人からも他の人へのルートがあり、誰も孤
立状態にはなっていない。但し、繋ぐ直線は円内では交わらないことにしておく。

　例えば、ｎ＝３　なら、

　　　 1            1              1            1
                            　          
    2----3    ,  2----3     ,   2    3   ,   2----3

の４パターンある。

　ｎ＝４　なら、

　　 1----4         　　 1----4            1----4
     |    |                   |            | ／
     2----3      ,       2----3     ,      2----3 ,  etc

　ただし、次の内部で交点が発生するものは含めない。

　　1----4
    | × |
    2----3

　さて、この条件で、円周上の点を直線で結ぶ場合、直線が交わらないで孤立点が発生し
ないルートの存在は、ｎ＝５、ｎ＝１１の場合、それぞれ何通り可能か？


（コメント）　ｎ＝４の場合のパターンは、全部で２３通りある。

実際に、

	のタイプが、	２通り	（０°回転、９０°回転）
	のタイプが、	１通り
	のタイプが、	４通り	（０°回転、９０°回転、１８０°回転、２７０°回転）
	のタイプが、	４通り	（０°回転、９０°回転、１８０°回転、２７０°回転）
	のタイプが、	４通り	（０°回転、９０°回転、１８０°回転、２７０°回転）
	のタイプが、	４通り	（０°回転、９０°回転、１８０°回転、２７０°回転）
	のタイプが、	２通り	（０°回転、９０°回転）
	のタイプが、	２通り	（０°回転、９０°回転）

　以上から、求めるパターンは、２３通りあることが分かる。

　同様にして、ｎ＝５の場合を考えてみよう。

　　　

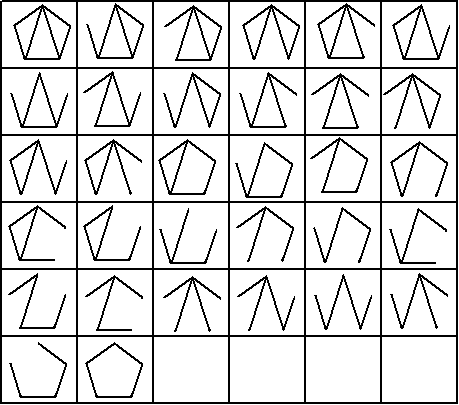
　最後の正５角形は１通りで確定だが、それ以外は回転により５通りずつの可能性があるの
で、起こり得るパターンは全部で、

　　３１×５＋１＝１５６（通り）

ある。（数え漏れがあるかもしれないので、全く自信なしです．．．。）

　ｎ＝６、７、８、９、１０、１１、・・・　も同様にやれば出来ると思うが、すごく大変そう．．．。
何かしら別な求め方はないのだろうか？


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年８月１０日付け）

　ＧＡＩ さん、n=11の場合、全部で 49826712 パターンですか？

#計算をしませんでした。


　ＧＡＩ さんからのコメントです。（令和３年８月１１日付け）

　そうです。（→　参考：「A007297」）

　実は、これを見つけたのが、最初オイラリアン数(A008292)を調べているとき、これが深く
polylog関数と関連していることに着目し、今度はこのpolylog関数で、

gp > polylog(-1,x)
%223 = x/(x^2 - 2*x + 1)

に対する展開式が、

gp > Ser(polylog(-1,x))
%224 = x + 2*x^2 + 3*x^3 + 4*x^4 + 5*x^5 + 6*x^6 + 7*x^7 + 8*x^8 + 9*x^9 + 10*x^10
　　　　　　　　　　 + 11*x^11 + 12*x^12 + 13*x^13 + 14*x^14 + 15*x^15 + 16*x^16 + O(x^17)

これの逆関数を見るために、

gp > serreverse(%224)
%225 = x - 2*x^2 + 5*x^3 - 14*x^4 + 42*x^5 - 132*x^6 + 429*x^7 - 1430*x^8 + 4862*x^9
　　　　　　 - 16796*x^10 + 58786*x^11 - 208012*x^12 + 742900*x^13 - 2674440*x^14
　　　　　　　　 + 9694845*x^15 - 35357670*x^16 + O(x^17)

すると、これはカタラン数（binomial(2*n,n)/(n+1))とまた深く関係していることが面白く、つい
でに、

gp > Ser(polylog(-2,x))
%226 = x + 4*x^2 + 9*x^3 + 16*x^4 + 25*x^5 + 36*x^6 + 49*x^7 + 64*x^8 + 81*x^9
　　　　　　 + 100*x^10 + 121*x^11 + 144*x^12 + 169*x^13 + 196*x^14 + 225*x^15
　　　　　　　　　 + 256*x^16 + O(x^17)

これに対する逆関数から、

gp > serreverse(%226)
%227 = x - 4*x^2 + 23*x^3 - 156*x^4 + 1162*x^5 - 9192*x^6 + 75819*x^7 - 644908*x^8
　　　　　　 + 5616182*x^9 - 49826712*x^10 + 448771622*x^11 - 4092553752*x^12
　　　　　　　　 + 37714212564*x^13 - 350658882768*x^14 + 3285490743987*x^15
　　　　　　　　　　　 - 30989950019532*x^16 + O(x^17)

　この係数に対する列をOEISで検索したら、例のA007297を引き当てた。

　この数字を眺めていたらオリンピックで熱戦を繰り広げていたサッカーやバスケの映像が
沸き起こったので出題していました。

　n=5までは何とか手作業でできるでしょうが、n=11ではとても無理ですね。


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年８月１１日付け）

　A263843 Reversion of g.f. for A162395 (squares with signs).

というのも凄く不思議ですね。



　　以下、工事中！