GAI さんからのコメントです。(令和3年2月16日付け)
(-cos(π/7),±sin(π/7))、(-cos(3*π/7),±sin(3*π/7))、(-cos(5*π/7),±sin(5*π/7))、(1,0)
#でも、sqrt(7)*y=4*x^2-x-3 は、どうやって発見できるんだろう?
らすかるさんからのコメントです。(令和3年2月16日付け)
y=ax^2+bx+c が、
(1,0)、(-cos(π/7),sin(π/7))、(-cos(3π/7),-sin(3π/7))、(-cos(5π/7),-sin(5π/7))
の4点を通るとすると、
a+b+c=0 … (1)
{(cos(π/7))^2}a-(cos(π/7))b+c=sin(π/7) … (2)
{(cos(3π/7))^2}a-(cos(3π/7))b+c=sin(-3π/7) … (3)
{(cos(5π/7))^2}a-(cos(5π/7))b+c=sin(-5π/7) … (4)
(2)+(3)+(4)から、 (5/4)a-(1/2)b+3c=-√7/2 … (5)
(1)と(5)から、 (a,b,c)=(2/√7-2t,t,-2/√7+t)
(2)に代入して整理すると、
t={sin(π/7)-(2/√7)(cos(π/7))^2+2/√7}/{-2(cos(π/7))^2-cos(π/7)+1}=-1/√7
よって、a=2/√7-2t=4/√7、b=t=-1/√7、c=-2/√7+t=-3/√7 なので、
y=(4/√7)x^2-(1/√7)x-(3/√7)=(4x^2-x-3)/√7 (途中計算はWolframAlphaを使用)
ちなみに、元ネタはこちら。
#正七角形には、いろいろ面白い性質がありますね。
DD++さんからのコメントです。(令和3年2月17日付け)
y 軸に平行な軸をもつ放物線って、一般には任意の 4 点を通るようにはできないはずな
んですが、今回の場合は過剰系がちゃんと解を持つんですね。
円周を 7 等分していることが何かうまく作用しているのでしょうか?
らすかるさんからのコメントです。(令和3年2月17日付け)
そうですね。任意の4点では無理です。でも、
「同一円周上の点で、4点を2点ずつに分けてそれぞれを直線で結んだときの2直線の傾きの
和が0」
という条件を満たす場合は、その4点を通る放物線が描けます。
(すなわち、3点を通る放物線が「放物線の交点」内の定理により必ず残りの点を通る)
正七角形には(1頂点が軸上にあれば)それを満たす性質がある、ということですね。
(追記) 1頂点はx軸上に限らず、y軸上にあってもよいので、(0,1)を通る場合も計算してみ
ました。その結果、2放物線は、y=-4x^2±(√7)x+1
(一つにまとめると、 (y+4x^2-1)^2=7x^2)
となり、2放物線の向きが揃っていて最高次の係数も整数なので、(似たようなもので
はありますが)、こちらの方が少し綺麗に感じました。
(0,-1)を通るようにすると、y=4x^2±(√7)x-1となり、最高次の係数が自然数になります。
DD++さんからのコメントです。(令和3年2月17日付け)
なるほど。さらに掘り下げると、円の中心から見て x 軸正方向から測った 4 点までの角度
の合計が 2π の整数倍になっていればいいわけですかね。
今回で言うと、
上に凸の放物線が 0+(2/7)π+(4/7)π+(8/7)π = 2π
下に凸の放物線が 0+(6/7)π+(10/7)π+(12/7)π = 4π
その発想を使うと、正七角形以上の正多角形全部でいろいろ遊べそうですね。
(追記) 「交点の座標」と題して、HN「GAI」さんからご投稿いただきました。
(令和3年2月18日付け)
方程式 11*y^2=(32*x^5-48*x^3+17*x-1)^2 のグラフと単位円との交点の座標は?
αさんからのコメントです。(令和3年2月18日付け)
WolframAlphaによる計算 交点の状況は下図参照。
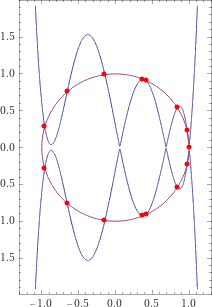
らすかるさんからのコメントです。(令和3年2月19日付け)
基本 (cos(2nπ/11),sin(2nπ/11)) ですが、余計な交点が4つありますね。でも、調べて
みたら、方程式が整数で書けるようにすると、どうしても余計な交点が出来てしまうみたい
ですね。
GAIさんからのコメントです。(令和3年2月19日付け)
計算し終わり、グラフソフトで描かせて見たら、バッチリ11等分点を通過していると思い込
みアップしたら、αさんからの投稿で、「アレー、微妙に余計な交点が存在しているんだ!」
と愕然となりました。
その後何とか余計な交点が排除できないものかと悪戦苦闘しましたが、分かりませんでし
た。
そんな試みの中に、(1,0) の地点は後から追加すると考えて、他の10点をすべて通れる
曲線を作ると、
11*y^2=(16*x^4+16*x^3-12*x^2-11*x+2)^2
なるものが出来ましたが、やはり、2か所の余計な交点が発生しました。係数が整数でない
もので、純粋に11等分点しか交わらない曲線はあるのですか?
y=±(3.1455465742*x^5-1.3789585964*x^4-7.1045673910*x^3
+2.0503750632*x^2+3.7981488890*x-0.5105445391)
で、純粋に11点の交点を通過するようです。(係数はあくまでも近似)
らすかるさんからのコメントです。(令和3年2月19日付け)
全く美しくない解答ですが、ちょっとズルをすれば整数でもできますね。
32x^6-16x^5-48x^4+20x^3+18x^2-5x-1=0 (y軸平行な6直線)
と単位円は、11等分点だけで交わります。
(追記) 後で思いついたのですが、上記の
32x^6-16x^5-48x^4+20x^3+18x^2-5x-1=0 (y軸平行な6直線)
と 1024y^11-2816y^9+2816y^7-1232y^5+220y^3-11y=0 (x軸平行な11直線)
を描いてうまく交点を選べば(x^2+y^2=1である交点を選べば)、正11角形の頂点になってい
ますね。
(上記は当たり前のことではありますが、今までこういうことを考えたことがありませんでした)
GAIさんからのコメントです。(令和3年2月19日付け)
と言うことは、kを0.8≦k≦1なる任意の実数として、
1024y^11-2816y^9+2816y^7-1232y^5+220y^3-11y+k*(32x^6-16x^5-48x^4+20x^3+18x^2-5x-1)=0
(もしくは、
32x^6-16x^5-48x^4+20x^3+18x^2-5x-1=1024y^11-2816y^9+2816y^7-1232y^5+220y^3-11y
の式でも可能)
なる式をグラフ化すれば、連続した自分自身とも交わらず、正11角形の全頂点を縫うように
クネクネと曲がりくねりながら進む蛇の様なグラフが出来上がるわけですね。う〜ん 面白い!
らすかるさんからのコメントです。(令和3年2月19日付け)
0.76≦k≦1.18で大丈夫のようですが、この他に、0.53≦k≦0.59 と 3.1≦k とそれぞれの符
号反転値も大丈夫みたいですね。
(GRAPESでは境界値付近で細部が正しく描画されません)
GAIさんからのコメントです。(令和3年2月20日付け)
らすかるさんのアイデアを拝借し、kを0でないパラメータとして、次で定義される曲線群を
パラメータkを変化させながら動かしていくと、単位円で点(1,0)を一つの頂点とする各正多角
形の各頂点を必ず通過する様子が見れます。(その変化していく様は壮観です。)
これらにはグラフソフトが必要ですが無料で「Grapes」にて入手できます。
データパネルの関係式に、これらの式を打ち込み(コピー&ペーストでも可)、自動的にパ
ラメータkを変化させるパネルも現れますので、値をスライドさせ、連動してグラフも変化して
いきます。
前もって基本図形パネルの中に点を作る機能がありますので、各正多角形の頂点になり
える位置、正五角形ならi=0,1,2,3,4とする5点(cos(i*2*Pi/5),sin((i*2*Pi/5))を定義して、単位
円上に丸印を付けておけばいいかも。
正三角形: 2*x^2-x-1=k*(4*y^3-3*y)
正四角形: x^3-x=k*(y^3-y)
正五角形: 4*x^3-2*x^2-3*x+1=k*(16*y^6-20*y^4+5*y^2)
正六角形: 4*x^4-5*x^2+1=k*(4*y^3-3*y)
正七角形: 8*x^4-4*x^3-8*x^2+3*x+1=k*(64*y^7-112*y^5+56*y^3-7*y)
正八角形: 2*x^5-3*x^3+x=k*(2*y^5-3*y^3+y)
正九角形: 16*x^5-8*x^4-20*x^3+8*x^2+5*x-1=k*(256*y^9-576*y7+432*y^5-120*y^3+9*y)
正十角形: 16*x^6-28*x^4+13*x^2-1=k*(16*y^5-20*y^3+5*y)
らすかるさんからのコメントです。(令和3年2月20日付け)
違う色で正多角形を描いておくと見やすいと思います。正多角形は、陰関数に
r=cos(Pi/n)/cos(Pi/n-2Acos(cos(n@/2))/n)
を入力して、nを変化させれば、任意の正多角形が描けます。
GAIさんからのコメントです。(令和3年2月21日付け)
またまた驚きです。この式一つで正多角形が瞬時に作れる!あの各頂点を一つ一つ打ち
込んでいた手間は何だったんだですかね。これはご自身で編み出されたんですか?
この式を解析してみようと構造を探るんですが、確かに数値的には原点からの距離rは、こ
の式通りに変化するんですが、なぜこの式でそれが作り出せるかが、なんかこんがらがって
きて、モヤモヤ感がとれません。粗筋的でもいいですから解説してもらえませんか?
らすかるさんからのコメントです。(令和3年2月21日付け)
O(0,0)、A(1,0)、B(cos(2π/n),sin(2π/n)) とすると、△OABはOA=OB=1の二等辺三角形で
あり、ABの中点をMとすると、 OM=OAcos∠MOA=cos(π/n)
PがAB上の点のとき、 OPcos∠POM=OM なので、
OP=OM/cos∠POM=cos(π/n)/cos(π/n-θ)
よって、線分ABは、 r=cos(π/n)/cos(π/n-θ) と表されます。
あとは、0≦θ<2πに対して、
0≦θ<2π/nのとき、 α=θ
2π/n≦θ<4π/n のとき、 α=θ-2π/n
4π/n≦θ<6π/n のとき、 α=θ-4π/n
・・・
のようなαを作り出して、このαを線分ABの式のθに代入すれば、正n角形が作れますが、
対称性から、
0≦θ<2π/n のとき、 α=θ
2π/n≦θ<4π/n のとき、 α=4π/n-θ
4π/n≦θ<6π/n のとき、 α=θ-4π/n
6π/n≦θ<8π/n のとき、 α=8π/n-θ
・・・
のようにしても問題ありません。
y=arccos(cos(x))のグラフが、/\/\/\… のような形になって、
0≦x<π のとき、 y=x
π≦x<2π のとき、 y=2π-x
2π≦x<3π のとき、 y=x-2π
3π≦x<4π のとき、 y=4π-x
4π≦x<5π のとき、 y=x-4π
・・・
となることを利用して、これを縦横とも2/n倍にした α=(2/n)arccos(cos((n/2)θ)) として線
分ABの式のθにこのαを代入し、
r=cos(π/n)/cos(π/n-(2/n)arccos(cos((n/2)θ)))
のようにすれば正n角形が作れます。
# この解説を書いている間に、 r=cos(π/n)/cos(π/n-(2/n)arccos(cos((n/2)θ))) は
r=cos(π/n)/cos(π/n-(1/n)arccos(cos(nθ))) でもよいことに気づきました。つまり、
r=cos(π/n)/cos(π/n-2Acos(cos(nθ/2))/n) は、r=cos(π/n)/cos(π/n-Acos(cos(nθ))/n)
でOKで、こちらの方がわずかに短くなります。
GAI さんからのコメントです。(令和3年2月22日付け)
解説ありがとうございました。f(x)=Acos(cos(x))の関数を利用するなんて、とても思いつくも
のではなかったです。
連続性に難点を持つが、 r=cos(π/n)/cos(π/n(2frc(nθ/(2π))-1)) でも正多角形が描
けるようです。(frc(x):xの小数部分を取り出す関数)
りらひいさんからのコメントです。(令和3年2月25日付け)
曲線 f(x,y)+k*g(x,y)=0 は、2曲線 f(x,y)=0, g(x,y)=0 の交点を通るんですね。
ということは、 4x^2-x-3+(±√7)y+k(x^2+y^2-1)=0 は、4点
(1,0)、(cos(2π/7),±sin(2π/7))、(cos(4π/7),±sin(4π/7))、(cos(8π/7),±sin(8π/7))
を通る二次曲線になります。対称性をよくするために、kを2k-2でおきなおして、
2x^2-2y^2-x+(±√7)y-1+2k(x^2+y^2-1)=0
で考えると、
-1<k<1 で、双曲線(退化して2直線になる値が3つある)
k=±1 で、放物線
k<-1、1<k で、楕円
k→±∞ で、円
式に、xyの項が含まれていないので、二次曲線の軸がx軸、y軸に平行または垂直なのが
おもしろいです。
(参考) 正七角形と二次曲線(← アプリ「GeoGebra」が必要)
