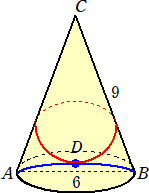
�@�@�̒����X�̒��~���ł���B���ʏ�ł`�a�����ԍŒZ���̒��_���c
�@�@�Ƃ���B
�@�@�@���ʏ�œ_�c��������`�b�A�a�b�ƌ����悤�ɋȐ��������A��
�@�@�Z�ƂȂ�悤�ɂ���B
�@�@�@���̂Ƃ��̋Ȑ��̒��������߂�B
�@�ߘa�R�N�Q���P�T���i���j�ɍs��ꂽ�_�ސ쌧�������Z�����̖�肪�����̐V��������
�f�ڂ��ꂽ�B���w�̖�肩��A���������������������������Ă݂��B��肪�����Ȃ�
�ŁA�v�_�������L���邱�Ƃɂ���B
��T�@�R�̔��o�A�p�A�q������A�o�ɂ́u�P�v�A�u�Q�v�A�u�S�v�̃J�[�h�A�p�ɂ́u�R�v�A�u�T�v�A�u�U�v�̃J
�@�@�@�[�h�������Ă��āA�q�ɂ͉��������Ă��Ȃ��B
�@�召�Q�̂�������𓊂��A�召�̂�������̖ڂ̐������ꂼ�ꂁ�A���Ƃ���B
�@�o���ڂ̐��ɂ���Ď��̑�����s���B
�y����P�z�@�J�[�h�ɏ����ꂽ���̍��v�����ƂȂ�悤�ɔ��o����P�`�Q���̃J�[�h�p�Ɉڂ��B
�y����Q�z�@���p�ɓ����Ă���J�[�h����A���̖ƂȂ�J�[�h��S�Ď��A���q�Ɉڂ��B
�i�A�j�@���q�ɓ����Ă���J�[�h���S���ƂȂ�m�������߂�B
�@�@�i���j�@��ӂ��A�����R�A�����U�@�̏ꍇ�݂̂Ȃ̂ŁA�m���́A�P/�R�U�@�@�i�I�j
�i�C�j�@���q�ɓ����Ă���J�[�h���P���ƂȂ�m�������߂�B
�@�@�i���j�@�S�Ă̏ꍇ���m�F����B
| ���_ | ���p�@�@�@�_�� | �P | �Q | �R | �S | �T | �U |
| �P | �P�C�R�C�T�C�U | �� | �� | �@ | �� | �@ | �@ |
| �Q | �Q�C�R�C�T�C�U | �@ | �� | �� | �� | �� | �@ |
| �R | �P�C�Q�C�R�C�T�C�U | �� | �@ | �@ | �@ | �@ | �@ |
| �S | �R�C�S�C�T�C�U | �@ | �@ | �� | �� | �� | �@ |
| �T | �P�C�R�C�S�C�T�C�U | �� | �� | �@ | �@ | �@ | �@ |
| �U | �Q�C�R�C�S�C�T�C�U | �@ | �� | �� | �@ | �� | �@ |
�@����āA���߂�m���́A�@�P�U/�R�U���S/�X�@�@�i�I�j
�i�R�����g�j�@���l�������Ă̊m���̖��B�����R�ꂪ�N�������ł��ˁB
�@���́A�~���̑��ʂ̍ŒZ����₤��Ԃ̖��ł��B����Ă���Γ�Ȃ����邱�Ƃ�
�ł���ł��傤�B
��U�i�E�j |
�@�@�@���}�͒����U�̐����`�a�a�Ƃ���~�n���ʂƂ��A����`�b �@�@�̒����X�̒��~���ł���B���ʏ�ł`�a�����ԍŒZ���̒��_���c �@�@�Ƃ���B �@�@�@���ʏ�œ_�c��������`�b�A�a�b�ƌ����悤�ɋȐ��������A�� �@�@�Z�ƂȂ�悤�ɂ���B �@�@�@���̂Ƃ��̋Ȑ��̒��������߂�B |
�i���j�@�W�J�}��`���ƁA
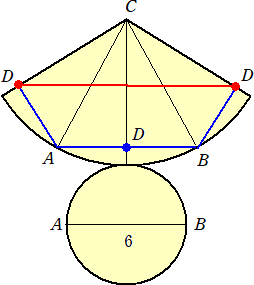 |
�@���}�ɂ����āA��ʂ̉~���̒����́A�U�Ȃ̂ŁA �@���ʂ̐�`�̒��S�p�̑傫���́A�P�Q�O���ł���B �@�@����āA�ڂ`�b�a���U�O���ƂȂ�A�b�c���X �@�ȏォ��A���}�̐Ԑ��̒����́A �@�@�@�i�X |
�@���͖ʐϔ䂩��̐����̒��������߂���ł��B�O�p�`�̖ʐςڋ��߂Ȃ��Ă�����
������ɂȂ��Ă��܂����A���ڋ��߂Ă������܂��B
��R�i�A�j�i�A�j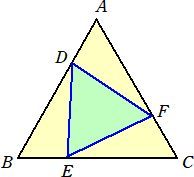 |
�@�@�@���}�̂悤�ɐ��O�p�`�`�a�b�̕ӂ`�a�A�a�b�A�b�`��ɂ��� �@�@����_�c�A�d�A�e���`�c���a�d���b�e�ƂȂ�悤�ɂƂ�B �@�@�@�`�a���P�W�ŁA�`�c���a�c�Ƃ���B���`�a�b�̖ʐςƁ��c�d�e�� �@�@�ʐς̔䂪�P�Q�F�V�ł���Ƃ��A�����`�c�̒��������߂�B |
�i���j�@�`�c���a�d���b�e�����@�Ƃ����ƁA�@�a�c���b�d���`�e���P�W�|��
�@���`�a�b���r�@�Ƃ���ƁA�@���c�d�e���r�|�i��/�P�W�j�r�~�i�P�W�|���j/�P�W�~�R���i�V/�P�Q�j�r
�@����āA�@�P�W�~�P�W�|�R���i�P�W�|���j���i�V/�P�Q�j�~�P�W�~�P�W�@���A
�@�@�@�P�O�W�|�P�W���{��2���U�R�@���Ȃ킿�A�@��2�|�P�W���{�S�T���O
�@�@�i���|�R�j�i���|�P�T�j���O
�@�`�c���a�c�@����A�@�����R�@�@�i�I�j
�@���̂悤�ȕʉ����l������B
�i�ʉ��j�@��ӂ��A�@���`�a�b�̖ʐρ��R�U�@�Ƃ���ƁA���c�d�e�̖ʐρ��Q�P
�@�@�@���̂Ƃ��A�@���`�c�e�����a�d�c�����b�e�d���T�@�ƂȂ�B
�@�����ŁA�@���`�c�d�����@�Ƃ����ƁA�@�i���{�T�j�~�i���{�T�j/�����R�U
�@����āA�@��2�|�Q�U���{�Q�T���O�@���A�@�����P�A�Q�T
�@�����Q�T�@�͕s�K�ŁA�@�����P
�@���������āA�@�`�c���P�W�~�i�P/�U�j���R�@�@�i�I�j
�i�ʉ��j�@�`�c�F�c�a���P�F���@�Ƃ����B���`�c�d���P�@�Ƃ���ƁA
�@�@�@���`�c�e�����a�d�c�����b�e�d�����@�ƂȂ�B
�@���̂Ƃ��A�@���`�a�b�����{�P�{���i���{�P�j���i���{�P�j2
�@���c�d�e���i���{�P�j2�|�R������2�|���{�P
�@��ӂ��A�@�i���{�P�j2 �F ��2�|���{�P���P�Q �F �V�@�Ȃ̂ŁA
�@�P�Q��2�|�P�Q���{�P�Q���V�i���{�P�j2 ���Ȃ킿�A�@�T��2�|�Q�U���{�T���O
�@�@�i�T���|�P�j�i���|�T�j���O�@���A�@�����P/�T�A�T
�@�@�`�c���a�c�@����A�����P/�T �͕s�K�ŁA�@�����T
�@����āA�@�`�c���P�W�~�i�P/�U�j���R�@�@�i�I�j
�@���̉s�����͎��̂悤�ɊȒP�ɓ��@����邩������Ȃ��B
�i�ʉ��j�@��ӂ��A�@���`�a�b�̖ʐρ��R�U�@�Ƃ���ƁA���c�d�e�̖ʐρ��Q�P
�@�@�@���̂Ƃ��A�@���`�c�e�����a�d�c�����b�e�d���T�@�ƂȂ�B
�@�����ŁA�@�`�c�F�c�a���P �F �T�@�Ƃ���ƁA�@���`�a�d���U�@�ƂȂ�A
�a�d �F �d�b���U �F �R�O���P �F �T�@�ő�ӂ����B
�@����āA�`�c���P�W�~�i�P/�U�j���R�@�@�i�I�j
�i�NjL�j�@�ߘa�S�N�Q���P�V���t��
�@�ߘa�S�N�Q���P�T���i�j�ɍs��ꂽ�_�ސ쌧�������Z�����̖�肪�����̐V��������
�f�ڂ��ꂽ�B���N�͓�Փx���啝�ɏオ��A�z�_������x�̖��ɏd�_�I�ɉ��_���ꂽ�B
�@���̒�����A���������������������������Ă݂��B���ɂ���Ă͉��肳��Ă���B
��R�i�A�j�i�A�j ���}�ɂ����āA�l�p�`�`�a�b�c�͕��s�l�ӌ`�Ƃ���B�ڂa�b�c�̓�����
�@�@�@�@�@�@�@�@�@�`�c�Ƃ̌�_���d�Ƃ��A�ӂa�b�̉�����ɓ_�e���A�b�e���c�e�ƂȂ�悤�ɂƂ�B
�@�@�@�@�@�@�@�@�@���A�l�p�`�b�e�c�d�����s�l�ӌ`�̂Ƃ��A�ڂ`�a�b�̑傫�������߂�B
�@�@�@�@�@�@
�i���j�@��}�ɂ����āA�@�Q���{�����P�W�O���A���{�Q�����P�W�O��
�@�@���̂Ƃ��A�ӁX�����āA�@�R���{�R�����R�U�O�����A�@���{�����P�Q�O��
�@�ӁX�����āA�@���|�����O�@���A�@�������@�Ȃ̂ŁA�@�����U�O��
�@����āA�@�ڂ`�a�b�������U�O���@�@�i�I�j
��R�i�E�j�@���}�̂悤�ɁA�~�n�̎���̓_�`�A�a�A�b�A�c�A�d �ɂ��āA�a�d�Ƃb�c�͕��s�ŁA
�@�@�@�@�@�@�����`�c�́ڂa�c�d�̓����ł���B
�@�@�@�@�@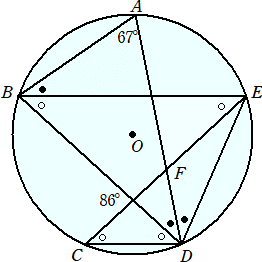
�@�����`�c�Ɛ����b�d�̌�_���e�Ƃ���Ƃ��A�ڂ`�e�d�̑傫�������߂�B
�i���j�@��}���A�@�Q�����W�U�����A�@�����S�R��
�@�@�܂��A�@�Q���{���{�U�V�����P�W�O�����A�@�����R�T��
�@����āA�@�ڂ`�e�c���P�W�O���|�Q���|�����T�X���@�@�i�I�j
�i�NjL�j�@�ߘa�S�N�Q���P�W���t��
��R�i�G�j�@���}�ɂ����āA�����`�a�͉~�n�̒��a�ł���A�Q�_�b�A�c�͉~�n�̎���̓_�ł���B
�@�@�@�@�@�@�܂��A�_�d�͐����`�b��̓_�ŁA�a�b�Ƃc�d�͕��s�ł���A�_�e�͐����`�a�Ɛ����c�d��
�@�@�@�@�@�@�̌�_�ł���B
�@�@�@�@�@�@�@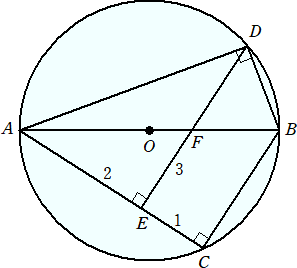
�@�@���A�`�d���Q�A�b�d���P�A�c�d���R�̂Ƃ��A���a�c�e�̖ʐς����߂�B
�i���j�@���}�̂悤�ɁA�����c�d���������~�n�Ƃ̌�_���f�Ƃ����B
�@�@�@�@�@�@
�@���̂Ƃ��A���ׂ��̒藝���A�@�R�~�d�f���Q�~�P�@�Ȃ̂ŁA�@�d�f���Q/�R
�@�܂��A���`�c�d�ɂ����āA�O�����̒藝���A�@�`�c��![]() �@�ł���B
�@�ł���B
�@���`�d�f�䁢�`�c�a�@���A�@�Q �F �Q/�R��![]() �F �c�a�@�Ȃ̂ŁA�@�c�a��
�F �c�a�@�Ȃ̂ŁA�@�c�a��![]() /�R
/�R
�@���������āA�@���`�c�e��![]() �~
�~![]() /�R���Q���P�R/�U�@�ƂȂ�B
/�R���Q���P�R/�U�@�ƂȂ�B
�@�`�e �F �e�d���Q �F �P�@�Ȃ̂ŁA�@���a�c�e���i�P�R/�U�j�~�i�P/�R�j���P�R/�P�W�@�@�i�I�j
�i�R�����g�j�@���ɂ��A���̖�肪��ԓ�������炵���B��@�͑��ɂ��������l
�@�@�@�@�@�@�����A���w�������Ɋy���ގ҂ɂƂ��ẮA�ǖ�̕��ނɓ���̂��낤�B�����A
�@�@�@�@�@�@����ꂽ���ԂŌ��ʂ��o���Ȃ���Ȃ�Ȃ����ɂƂ��ẮA�����u�̂Ė�v
�@�@�@�@�@�@�ƂȂ炴��Ȃ������悤���B
�i�NjL�j�@�ߘa�S�N�Q���P�X���t��
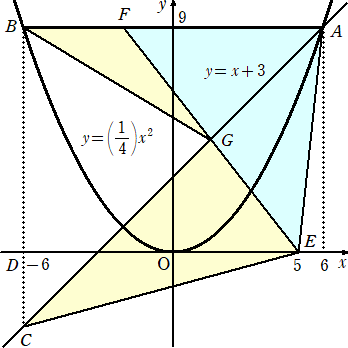
��S�i�E�j�@���}�̂悤�ɕ����� �����i�P/�S�j��2 �ƒ��� �������{�R ��������Ă���B�܂��A
�@�@�@�@�@�@�`�i�U�C�X�j�A�a�i�|�U�C�X�j�A�b�i�|�U�C�|�R�j�A�c�i�|�U�C�O�j�A�d�i�T�C�O�j�ł���B
�@�@�����`�a��̓_�e���A���`�d�e�̖ʐς����� �������{�R �ɂ���ĂQ���������悤�ɂƂ�A
�@���� �������{�R �Ɛ����d�e�Ƃ̌�_���f�Ƃ���B
�@�@�@�@
�@���̂Ƃ��A���̖₢�ɓ�����B
�i�P�j�@�e�A�f �̍��W�����߂�B
�i�Q�j�@���a�f�e �F ���b�d�f ���ł��ȒP�Ȑ�����ŕ\���B
�i���j�i�P�j�@�e�i���C�X�j�A�f�i���|�R�C���j�Ƃ����ƁA��ӂ��A
�@�i�U�|���j�i�X�|���j/�Q���i�U�|���j�E�X/�Q�E�i�P/�Q�j�@���A�@�Q�i�X�|���j���X�@�Ȃ̂ŁA�@�����X/�Q
�@����āA�@�f�i�R/�Q�C�X/�Q�j�@�ł���B
�@���̂Ƃ��A�����d�f�̕������́A�@�����i�|�X/�V�j���{�S�T/�V�@�Ȃ̂ŁA�����X�Ƃ����ƁA
�@�i�|�X/�V�j���{�S�T/�V���X�@�������āA�@�����|�Q�@�@����āA�@�e�i�|�Q�C�X�j�@�ł���B
�i�Q�j�@�i�P�j���A�@���a�f�e���S�E�i�X�|�X/�Q�j�E�i�P/�Q�j���X�@�ƂȂ�B
�@�܂��A
�@���b�d�f���i�R/�Q�{�U�j�i�X/�Q�{�R�j/�Q�{�i�X/�Q�{�R�{�R�j�i�T�|�R/�Q�j/�Q�|�i�T�{�U�j�E�R/�Q
�@�@�@�@�@ ���Q�Q�T/�W�{�P�S�V/�W�|�R�R/�Q���R�O
�Ȃ̂ŁA�@���a�f�e �F ���b�d�f���X �F �R�O���R �F �P�O�@�ł���B�@�@�i�I�j
�i�R�����g�j�@���b�d�f�̖ʐς̌v�Z�ł́A���̂悤�ȕ��@������ł��傤�B
�@���`�e�f���i�U�{�Q�j�i�X�|�X/�Q�j/�Q���P�W�@�ł���B
�@�`�b����i�P�Q2�{�P�Q2�j���P�Q![]()
�@���� �������{�R�@�Ɠ_�i�T�C�O�j�Ƃ̋����́A�S![]() �@�Ȃ̂ŁA�@���`�b�d���S�W
�@�Ȃ̂ŁA�@���`�b�d���S�W
�@����āA�@���b�d�f���S�W�|�P�W���R�O�@�ł���̂ŁA
�@���a�f�e �F ���b�d�f���X �F �R�O���R �F �P�O�@�ł���B
�@�܂��A��L�ł͖ʐςڌv�Z���āA���a�f�e �F ���b�d�f�@�����߂����A�ʐς��v�Z���Ȃ���
���悢�悤�ł���B
�@���ۂɁA���a�f�e���r�@�Ƃ����ƁA�@�`�e �F �e�a���W �F �S���Q �F �P�@�Ȃ̂ŁA�@���`�f�e���Q�r
�@�܂��A��ӂ��A�@���`�d�f���Q�r�@�ŁA�@�`�f �F �f�b���U�|�R/�Q �F �R/�Q�{�U���R �F �T�@���A
�@���b�d�f���i�T/�R�j�E�Q�r���i�P�O/�R�j�r�@�Ȃ̂ŁA
�@���a�f�e �F ���b�d�f���r �F �i�P�O/�R�j�r���R �F �P�O�@�ł���B
�i�NjL�j�@�ߘa�S�N�Q���Q�O���t��
��T�i�C�j�@�������P�O�̐����o�p������B��A���Q�̂�������𓊂��A�傫����������̖ڂ�
�@�@�@�@�@�@���A��������������̖ڂ����Ƃ���B�����o�p��ɓ_�q���A�o�q �F �q�p���� �F ���@�ƂȂ�
�@�@�@�@�@�@�悤�ɂƂ�B�����o�q���P�ӂƂ��鐳���`�̖ʐς��w�A�����q�p���P�ӂƂ��鐳���`
�@�@�@�@�@�@�̖ʐς��x �Ƃ����B���̂Ƃ��A�w���x�{�Q�T �ƂȂ�m�������߂�B
�i���j�@�w���i�P�O��/�i���{���j�j2�@�A�x���i�P�O��/�i���{���j�j2�@�Ȃ̂ŁA
�@�@�@�i�P�O��/�i���{���j�j2���i�P�O��/�i���{���j�j2�{�Q�T
�@�i�P�O��/�i���{���j�j2�|�i�P�O��/�i���{���j�j2���P�O�O�i���|���j/�i���{���j�@����A
�@�@�@�P�O�O�i���|���j/�i���{���j���Q�T�@�@���Ȃ킿�A�@�S�i���|���j���i���{���j�@���A�@�R�����T��
�@�����P�@�̂Ƃ��A�@�����Q�A�R�A�S�A�T�A�U
�@�����Q�@�̂Ƃ��A�@�����S�A�T�A�U
�@�����R�@�̂Ƃ��A�@�����T�A�U
�@����āA���߂�m���́A�@�P�O/�R�U���T/�P�W�@�@�i�I�j
�i�NjL�j�@�ߘa�S�N�Q���Q�P���t��
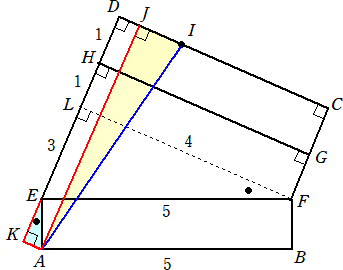
��U�i�E�j�@���}�́A�`�a���T�A�a�b���P�A�`�c���S�A�ڂ`�c�b���ڂa�b�c���X�O���̑�`�`�a�b�c��
�@�@�@�@�@�@��ʂƂ��A�`�d���a�e���b�f���c�g���P�������Ƃ���l�p���ł���B
�@�@�@�@�@
�@�@�ӂb�c��ɁA�b�h �F �h�c���V �F �R �ł���悤�ɓ_ �h ���Ƃ�A���̎l�p���̕\�ʏ�ɓ_�`����_
�@�h �܂ŕӂd�e�A�ӂf�g�ƌ����悤�ɐ��Ō��ԁB���̂悤�Ȑ��̂����A�������ł��Z���̂͂���
�@���H
�i���j�@��}�̓W�J�}��`���ƁA���߂���̂͐����`�h �̒����ł���B
�@�@
�@�b�h �F �h�c���V �F �R �Ȃ̂ŁA�@�h�c���S�~�i�R/�P�O�j���U/�T
�@�܂��A�@���k�d�e�䁢�j�`�d�@���A�@�j�d���P�~�i�S/�T�j���S/�T�@�A�@�`�j���P�~�i�R/�T�j���R/�T
�@����āA���`�h�i�ɂ����āA�O�����̒藝���A
�@�@�`�h2���i�U/�T�|�R/�T�j2�{�i�T�{�S/�T�j2���i�X�{�W�S�P�j/�Q�T���R�S�@�Ȃ̂ŁA
�@�`�h��![]() �@�ł���B�@�@�i�I�j
�@�ł���B�@�@�i�I�j
�i�NjL�j�@�ߘa�T�N�Q���P�T���t��
�@�ߘa�T�N�Q���P�S���i�j�ɍs��ꂽ�_�ސ쌧�������Z�����̖�肪�����̐V��������
�f�ڂ��ꂽ�B��N�x�͋}���ɓ���������A���N�x�����̌X���͕ς�炸�A��������悤
���B���ɁA��b�͂̂Ȃ����ɂƂ��Ă͌����������ƂȂ����͗l���B
�@�����ŁA���������������������������Ă݂��B���ɂ���Ă͉��肳��Ă���B
��Q�i�G�j�@�\�ʂ��S�̂R���̎��R���̕S�ʂƈ�ʂ���ꂩ�������́A���̐����R�X�U�傫
�@�@�@�@�@�@���B���̐��̕S�ʂƈ�ʂ̐��̘a���P�O�̂Ƃ��A���̐��̈�ʂ̐������߂�B
�i���j�@���̎��R���́@�P�O�O���{�S�O�{���@�Ə�����B
�@�@��ӂ��A�@�i�P�O�O���{�S�O�{���j�|�i�P�O�O���{�S�O�{���j���X�X�i���|���j���R�X�U
�@����āA�@���|�����S�@�ŁA�܂��A�@���{�����P�O�@���A�@�����V�@�ł���B�@�@�i�I�j
��R�@���̖₢�ɓ�����B
�i�A�j�@���}�̂悤�ɁA�����`�a�a�Ƃ���~�n�̎���ɁA�Q�_�`�A�a�Ƃ͈قȂ�_�b��
�@�@�@�`�b���a�b�ƂȂ�悤�ɂƂ�A�����`�a�Ɋւ��ē_�b�ƑΏ̂ȉ~����̓_���c�Ƃ����B�܂��A
�@�@�@�_�`���܂܂Ȃ��ʂa�c��ɁA�Q�_�a�A�c�Ƃ͈قȂ�_�d���Ƃ�A�`�a�Ƃb�d�A�`�d�Ƃa�c�A�a�c��
�@�@�@�b�d�̌�_�����ꂼ��e�A�f�A�g�Ƃ����B����ɁA�_�`���a�c�ɕ��s���������A�b�d�Ƃ̌�
�@�@�@�_���h�Ƃ����B
�@�@�@
�@���̂Ƃ��A���́i�@�j�i�A�j�ɓ�����B
�i�@�j�@���`�h�e�䁢�d�g�f�@�ł��邱�Ƃ������B
�i�A�j�@�ڂa�c�d���R�T���A�ڂc�a�d���Q�W���̂Ƃ��A�ڂb�`�h �̑傫�������߂�B
�i���j�i�@�j�@���`�h�e�Ɓ��d�g�f�ɂ��āA�c�a�Ƃ`�h �͕��s�Ȃ̂ŁA���s���̓��ʊp�͓������̂ŁA
�@�ڂ`�h�d���ڂc�g�d�@���Ȃ킿�A�@�ڂ`�h�e���ڂd�g�f�@�E�E�E�@�@
�@���ɁA������A�@�ڂ`�a�b���ڂ`�a�c�@�E�E�E�@�A
�@�܂��A�ʂ`�b�ɑ���~���p�͓���������A�@�ڂ`�a�b���ڂ`�d�b�@�E�E�E�@�B
�@����ɁA�c�a�Ƃ`�h �͕��s�Ȃ̂ŁA���s���̍��p�͓���������A�@�ڂ`�a�c���ڂa�`�h�@�E�E�E�@�C
�@�A�A�B�A�C���A�@�ڂa�`�h���ڂ`�d�b�@�Ȃ̂ŁA�@�ڂe�`�h���ڂf�d�g�@�E�E�E�@�D
�@�@�A�D���A�Q�g�̊p�����ꂼ�ꓙ�����̂ŁA�@���`�h�e�䁢�d�g�f�@�ł���B
�i�R�����g�j�@�\�ߗ^����ꂽ�ؖ����A�u�ڂ`�d�b���ڂa�`�h�v�Ƃ��邪�A�Ή�����O�p�`�̊p�̑�
�@�@�@�@�@�@�������l���āA�u�ڂa�`�h���ڂ`�d�b�v�Ƃ��ׂ����낤�B�i��������ƋC�ɂȂ����I�j
�i�A�j�@�ڂa�c�d���R�T�����A�ڂa�b�d���R�T���@�܂��A�ڂa�b�`���X�O������A�ڂ`�b�d���T�T��
�@���Ȃ킿�A�@�ڂ`�a�d���T�T���@�Ƃ���ŁA�@�ڂc�a�d���Q�W�����A�@�ڂ`�a�c���Q�V��
�@����āA�@�ڂa�`�h���Q�V���ŁA�ڂ`�d�b���Q�V���@�܂��A�ڂ`�d�a���X�O�����A�ڂa�d�b���U�R��
���������āA�@�ڂa�`�b���U�R�����A�@�ڂb�`�h���U�R���|�Q�V�����R�U���@�@�i�I�j
�i�E�j�@�w�Z����w�܂ł̓��̂�͂Q�S�O�O���ŁA���̓r���Ɂu�����ߐ}���فv�Ɓu�����傤�}��
�@�@�@�فv������B�`�A�a�̂Q�l���P�U���Ɋw�Z���o�����A���ꂼ�ꂪ�}���قɗ�������Ă���
�@�@�@�w�܂ňړ����钆�ň�x�����������A�w�ɂ͓����ɓ��������B
�@�`�́u�����ߐ}���فv�ɂT���ԗ�������Ė{����A�w�܂ňړ������B�a�́u�����傤�}���فv
�ɂP�T���ԗ�������Ď肽���{��T������������Ȃ��������ߓ��������Ԃ��A�u�����ߐ}
���فv�ɂT���ԗ�������Ė{����A�w�܂ňړ������B
�@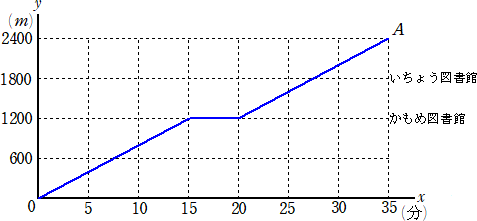
�@���̂Ƃ��A�ړ����̂`�A�a�̑����͈��Ƃ��A�`�A�a�������������ԑт��߂�B
�i���j�@�a�́A�R�T�|�P�T�|�T���P�T�i���j�ŁA�P�W�O�O�{�U�O�O�{�P�Q�O�O���R�U�O�O�i���j���ړ�������
�@�ŁA�ړ��̑����́A�@�R�U�O�O���P�T���Q�S�O�@���A�����Q�S�O���ł���B
�@����āA�a�̈ړ���Ԏ����Ŏ����A���}�̂悤�ɂȂ�B
�@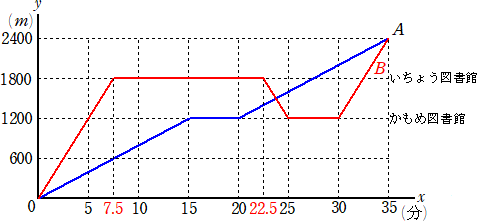
�@��}�̃O���t����A�`�A�a�������������ԑт́A�P�U���Q�R������P�U���Q�T���܂ł̊Ԃ�
�Ȃ�B�@�@�i�I�j
�i�R�����g�j�@�a�̈ړ��̑����������Q�S�O���Ƃ������Ƃ́A�����P�S�D�S�����Ȃ̂ŁA�a�͎��]��
�@�@�@�@�@�@�ňړ������̂��낤�B
�@��肪�v������͎̂��ԑтȂ̂ŁA�O���t���`����Όv�Z����܂ł��Ȃ����_�͓����
��B�ȉ��ŁA��̓I�ɂ���Ⴄ���Ԃ���肵�悤�B
�@�`�A�a������Ⴄ�O��ł̒����̕����������߂�A
�@�`�́A�@�����i�Q/�R�j�i���|�S�j�{�Q���i�Q/�R�j���|�i�Q/�R�j
�@�a�́A�@�����|�Q�i���|�T�j�{�Q���|�Q���{�P�Q
�ƂȂ�̂ŁA�A�����āA�@�i�Q/�R�j���|�i�Q/�R�j���|�Q���{�P�Q�@���A�@�@�����P�X/�S
�@����āA����Ⴄ���Ԃ́A�w�Z���o�����Ă���@�i�P�X/�S�j�~�T���X�T/�S���Q�R�D�V�T�i����j
���@���ƂȂ��A�������w�����̎Z���̖����ۂ����͋C�ł����ˁI
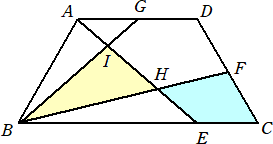
�i�G�j�@���}�ɂ����āA�l�p�`�`�a�b�c�� �`�a���b�c���c�`�A�`�a �F �a�b���P �F �Q �̑�`�ł���B
�@�@�@�܂��A�_�d�͕ӂa�b��̓_�ŁA�a�d �F �d�b���R �F �P �ł���A�Q�_�e�A�f�͂��ꂼ��ӂb�c�A
�@�@�@�c�`�̒��_�ł���B����ɁA�����`�d�Ɛ����a�e�Ƃ̌�_���g�A�����`�d�Ɛ����a�f�Ƃ̌�
�@�@�@�_�� �h �Ƃ���B���̂Ƃ��A���a�g�h �Ǝl�p�`�b�e�g�d�̖ʐϔ���ł��ȒP�Ȑ����̔�ŕ\
�@�@�@���B
�@�@
�i���j�@���}�̂悤�ɕ⏕���������B
�@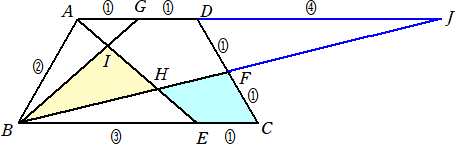
�@���̂Ƃ��A�@�`�h �F �h�d���P �F �R�@�A�`�g �F �g�d���U �F �R���Q �F �P�@�ł���̂ŁA
�@�`�h �F �h�g �F �g�d���R �F �T �F �S�@���A�@���a�g�h �F ���a�d�g���T �F �S
���l�ɂ��āA�@�a�g �F �g�i���R �F �U���P �F �Q�@�A�a�e �F �e�i���S �F �S���P �F �P�@���A
�@�a�g �F �g�e �F �e�i���Q �F �P �F �R�@�Ȃ̂ŁA�@���a�d�g �F ���a�b�e���U �F �P�Q���P �F �Q
�@����āA�@�l�p�`�b�e�g�d�̖ʐρ����a�d�g�@�����藧�̂ŁA���a�g�h �Ǝl�p�`�b�e�g�d�̖�
�ϔ�́A�@�T�F�S�@�ƂȂ�B�@�@�i�I�j
�i�R�����g�j�@���a�d�g �F ���a�b�e�@�̌v�Z�ŁA�����̔䂪�A�a�g �F �a�e���Q �F �R�@�ł��邱�Ƃ���A
�@�@���a�d�g �F ���a�b�e���Q�E�R �F �R�E�S���P �F �Q�@�ł���B
�@�O�p���p�����O�p�`�̖ʐς̌�����m���Ă���Ζ��炩�����A���w���ΏۂȂ̂ŁA
��L�̂悤�ȉ�@�ƂȂ�B
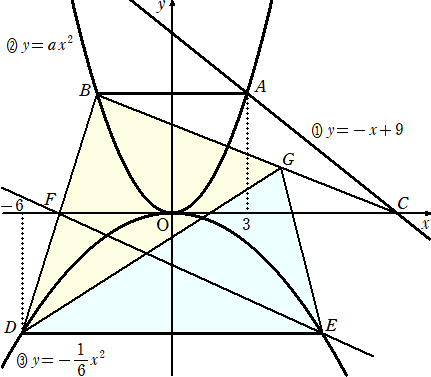
��S�@���}�ɂ����āA�����@�͊� �����|���{�X�@�̃O���t�ł���A�Ȑ��A�͊� ��������2
�@�@�@�̃O���t�A�Ȑ��B�͊� �����i�|�P/�U�j��2 �̃O���t�ł���B�_�`�͒����@�ƋȐ��A�Ƃ�
�@�@�@��_�ŁA���� �� ���W�͂R�ł���B�_�a�́A�Ȑ��A��̓_�ŁA�����`�a�� �� ���ɕ��s��
�@�@�@����B�_�b�͒����@�� �� ���Ƃ̌�_�ł���B�܂��A�Q�_�c�A�d�͋Ȑ��B��̓_�ŁA�_�c
�@�@�@�� �� ���W�́|�U�ł���A�����c�d�� �� ���ɕ��s�ł���B����ɁA�_�e�͐����a�c�� �� ��
�@�@�@�Ƃ̌�_�ł���B
�@�@�@�@
�@���_���n�Ƃ���Ƃ��A���̖₢�ɓ�����B
�i�A�j�@�� �̒l�����߂�B
�i�C�j�@�����d�e�̕����������߂�B
�i�E�j�@�����a�b��ɓ_�f���A���a�c�f�����c�d�f �ƂȂ�悤�ɂƂ�Ƃ��A�_�f�� �� ���W�����߂�B
�i���j�i�A�j�@�`�i�R�C�U�j�@�Ȃ̂ŁA�@�U���X���@����A�@�����Q/�R
�i�C�j�@�a�i�|�R�C�U�j�A�c�i�|�U�C�|�U�j�@���A�����a�c�̕������́A�@�����S���{�P�W
�@�@����āA�S���{�P�W���O�@���A�@�����|�X/�Q�@����A�@�e�i�|�X/�Q�C�O�j
�@�@�d�i�U�C�|�U�j�@�Ȃ̂ŁA�����d�e�̕������́A�@�����i�|�S/�V�j���|�P�W/�V
�i�E�j�@���}�̂悤�ɕ⏕���������čl����B
�@�@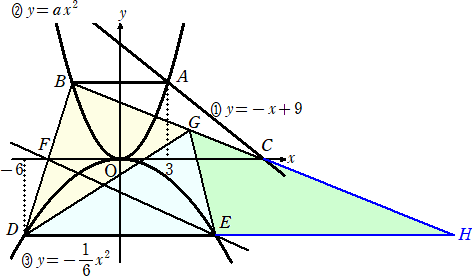
�@�a�i�|�R�C�U�j�A�b�i�X�C�O�j�@���A�����a�b�̕������́A�@�����i�|�P/�Q�j���{�X/�Q�@�Ȃ̂ŁA
�@�i�|�P/�Q�j���{�X/�Q���|�U�@���A�@�w���Q�P�@�@����āA�g�i�Q�P�C�|�U�j�ƂȂ�B
�@���̂Ƃ��A�@�c�d �F �d�g���P�Q �F �P�T���S �F �T�@�Ȃ̂ŁA���f�d�g���T�r�@�Ƃ����ƁA���c�d�f���S�r
��ӂ��A�@���a�c�f�����c�d�f���S�r�@�ƂȂ�̂ŁA�@���a�c�g���P�R�r�@�ƂȂ�B
�@�Ƃ���ŁA���a�c�g���Q�V�~�P�Q���Q���P�U�Q�@�Ȃ̂ŁA�@�P�R�r���P�U�Q�@����A�@�r���P�U�Q/�P�R
�@����āA���f�c�d���S�r���U�S�W/�P�R�@�ƂȂ�̂ŁA�f�� �� ���W�� �� �Ƃ��āA
�@�P�Q�i���{�U�j���Q���U�S�W/�P�R�@����A�@�����P�O�W/�P�R�|�U���R�O/�P�R
���̂Ƃ��A�@�i�|�P/�Q�j���{�X/�Q���R�O/�P�R�@���A�@�����T�V/�P�R�@�@�i�I�j
�i�R�����g�j�@��R�i�G�j�Ɠ��l�ȕ⏕�����l����p�^�[���́A�o��҂͂��D���炵���B�����A��
�@�@�@�@�@�l���������āA�����˘f�킹��̂ɏ\�����낤�B
�@�������āA�_�ƒ����̋����̌������g���悢�A�Ǝv�������̂́A����͒��w���̊w�K
�͈͂������̂Ȃ̂��S�O���Ă��܂��B�Q�l�܂łɁA���̉�@�ׂĂ݂��B
�i�ʉ��j�@�_�c��ʂ�A�X�����̒����̕������́A�������i���{�U�j�|�U�@���Ȃ킿�A
�@�����|���{�U���|�U���O�@�ł���B���̂Ƃ��A
�@�_�a�ƒ����̋����́A�@�R�b���|�S�b/��i��2�{�P�j
�@�_�d�ƒ����̋����́A�@�P�Q�b���b/��i��2�{�P�j
�@���a�c�f�����c�d�f �ƂȂ邽�߂ɂ́A�@�R�b���|�S�b/��i��2�{�P�j���P�Q�b���b/��i��2�{�P�j
���Ȃ킿�A�@�b���|�S�b���S�b���b�@�����藧�Ă悢�B
�@���̂Ƃ��A�@���|�S���}�S���@����A�����|�S/�R�@�A�S/�T�@�ł��邪�A�@�����|�S/�R�@�͕s�K
����āA�����c�f�̕������́A�@�����i�S/�T�j�i���{�U�j�|�U
�܂��A�����a�b�̕������́A�@�����i�|�P/�Q�j���{�X/�Q�@�Ȃ̂ŁA�A�����āA
�@�i�S/�T�j�i���{�U�j�|�U���i�|�P/�Q�j���{�X/�Q�@���A�@�����T�V/�P�R�@�@�i�I�j
��T�@���}�̂悤�ɁA�ꏊ�o�A�p�A�q������A�ꏊ�o�ɂ͂P�`�U�̐����P�������ꂽ�U��
�@�@�@�����̂̃u���b�N���A�����ꂽ�����̑傫�����̂��珇�ɁA�������Ɍ������Đς�
�@�@�@�����B
�@�@�@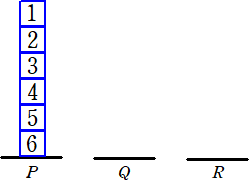
�@�召�Q�̂���������ɂP���A�傫����������̏o���ڂ̐��� ���A�������������
�o���ڂ̐��� �� �Ƃ���B�o���ڂ̐��ɂ���āA���́y����P�z�A�y����Q�z�����ɍs���A�ꏊ�o�A
�p�A�q�̂R�����ɂ���u���b�N�̌��ɂ��čl����B
�y����P�z�@�� �̃u���b�N����т��̏�̃u���b�N�����Ԃ�ς����ɏꏊ�p�ֈړ�����B
�y����Q�z�@�ꏊ�o�A�p�� �� �̃u���b�N����т��̏�̃u���b�N�����Ԃ�ς����ɏꏊ�q�ֈ�
�@�@�@�@�@�@������B
�@���A�召�Q�̂���������ɂP����Ƃ��A���̖₢�ɓ�����B
�i�A�j�@�u���b�N�̌����R�����Ƃ������ɂȂ�m�������߂�B
�i�C�j�@�R�����̂����A���Ȃ��Ƃ��P�����̃u���b�N�̌����O�ɂȂ�m�������߂�B
�i���j�i�P�j�@�N���蓾��ꍇ�́A�i���C���j���i�Q�C�S�j�A�i�S�C�Q�j�@�̂Q�ʂ�Ȃ̂ŁA
�@�@���߂�m���́A�@�Q/�R�U���P/�P�W
�i�Q�j�@�N���蓾��ꍇ�́A
�i���C���j���i�P�C�P�j�A�i�P�C�U�j�A�i�Q�C�Q�j�A�i�Q�C�U�j�A�i�R�C�R�j�A�i�R�C�U�j�A�i�S�C�S�j�A�i�S�C�U�j�A�i�T�C�T�j�A
�@�@�@�@�@�i�T�C�U�j�A�i�U�C�P�j�A�i�U�C�Q�j�A�i�U�C�R�j�A�i�U�C�S�j�A�i�U�C�T�j�A�i�U�C�U�j
�@�̂P�U�ʂ�Ȃ̂ŁA
�@�@���߂�m���́A�@�P�U/�R�U���S/�X�@�@�i�I�j
�i�R�����g�j�@�y����P�z�A�y����Q�z�̈Ӗ���������A�Ղ����m���̖��ł����B
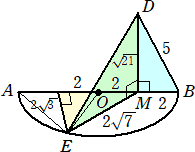
��U�@���}�́A�����`�a�a�Ƃ���~�n���ʂƂ��A�����`�b�����Ƃ���~�����ł���B
�@�@�@�_�c�͐����a�b�̒��_�ŁA�_�d�͉~�n�̎���̓_�ŁA�_�e�͐����`�b�̒��_�ł���B
�@�@�@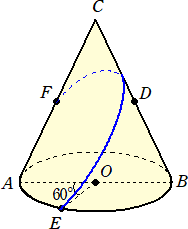
�@�`�a���W�����A�`�b���P�O�����A�ڂ`�n�d���U�O���̂Ƃ��A���̖₢�ɓ�����B
�i�A�j�@�~�����̕\�ʐς����߂�B
�i�C�j�@�Q�_�c�A�d�Ԃ̋��������߂�B
�i�E�j�@�~�����̑��ʏ�ɓ_�d��������a�b�ƌ����悤�ɓ_�e�܂Ő��������B���̂Ƃ��A����
�@�@�@�悤�Ȑ��̒����̍ŏ��l�����߂�B
�i���j�i�A�j�@�P�O�~�W���Q�{�P�U���T�U�i����2�j
�i�C�j�@���_�A���藝���A�@�n�c���T�@�Ȃ̂ŁA���c�n�a�͂Q���ӎO�p�`�ƂȂ�B�����n�a�̒�
�@�_���l�Ƃ����ƁA�@�c�l����i�T2�|�Q2�j����Q�P�@�ł���B
�@�܂��A�@�l�d2���i�Q![]() �j2�{�S2���Q�W�@�Ȃ̂ŁA�@�c�d2���c�l2�{�l�d2���S�X�@���A
�j2�{�S2���Q�W�@�Ȃ̂ŁA�@�c�d2���c�l2�{�l�d2���S�X�@���A
�@�c�d���V�i�����j�@�ƂȂ�B
�@�@�@�@
�i�E�j�@���ʂ�W�J���Đ�`�����ƁA���̒��S�p�́A�W��/�P�O���S��/�T�@�����A�P�S�S��
�@���̂Ƃ��A�@�ڂd�b�e���P�S�S���~�i�T/�U�j���P�Q�O���ƂȂ�B
�@�@�@�@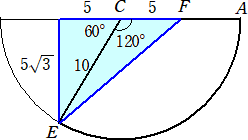
���̂Ƃ��A�@�d�e2���i�T![]() �j2�{�P�O2���P�V�T�@�Ȃ̂ŁA�@�d�e���T
�j2�{�P�O2���P�V�T�@�Ȃ̂ŁA�@�d�e���T![]() �i�����j�@�ƂȂ�B�@�@�i�I�j
�i�����j�@�ƂȂ�B�@�@�i�I�j
�i�R�����g�j�@�]���藝��m���Ă���A�@�d�e2���P�O2�{�T2�|�Q�E�P�O�E�T�E�i�|�P/�Q�j���P�V�T
�@�@�@�@�@�@����A�d�e���T![]() �i�����j�@�ł��邱�Ƃ͒����ɕ�����B
�i�����j�@�ł��邱�Ƃ͒����ɕ�����B
�i�NjL�j�@�ߘa�U�N�Q���P�U���t��
�@�ߘa�U�N�Q���P�S���i���j�ɍs��ꂽ�_�ސ쌧�������Z�����̖�肪�����̐V��������
�f�ڂ��ꂽ�B�Ƃ���ǂ���œ�������U������A��b�͂̂Ȃ����ɂƂ��Ă͌�����
�����ƂȂ����͗l���B���ϓ_�́A��N�ʂ�̌��ʂɂȂ�͗l�ł���B
�@�����ŁA���������������������������Ă݂��B���ɂ���Ă͉��肳��Ă���B
��R�@���̖₢�ɓ�����B
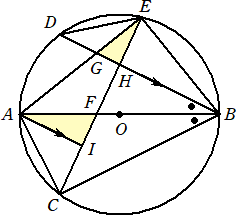
�i�A�j�@���}�̂悤�ɁA�~�n�̎���ɁA�قȂ�R�_�`�A�a�A�b���`�a���`�b�ƂȂ�悤�ɂƂ�B�܂��A
�@�@�_�`���܂܂Ȃ��ʂa�b��ɂQ�_�a�A�b�Ƃ͈قȂ�_�c���a�c���b�c�ƂȂ�悤�ɂƂ�A�����`�c
�@�@�Ɛ����a�b�Ƃ̌�_���d�Ƃ���B�����ɁA�ڂb�`�c�̂Q�������Ɖ~�n�Ƃ̌�_�̂����A�_�`��
�@�@�͈قȂ�_���e�Ƃ��A�����`�e�Ɛ����a�b�Ƃ̌�_���f�A�����`�e�Ɛ����b�c�Ƃ̌�_���g��
�@�@����B
�@�@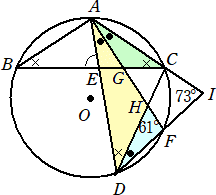
�@�����`�b�̉����Ɛ����c�e�̉����Ƃ̌�_�� �h �Ƃ���B�ڂ`�h�c���V�R���A�ڂc�g�e���U�P����
�Ƃ��A�ڂ`�d�a�̑傫�������߂�B
�i���j�@���`�e�h �ɂ����āA�@���{�i���{�U�P���j�{�V�R�����P�W�O�����A�@�����Q�R��
�@���`�c�g�@�ɂ����āA�@���{�~�{�i�P�W�O���|�U�P���j���P�W�O�����A�@���{�~���U�P��
�@����āA�@�~���R�W���ł���B
�@���̂Ƃ��A�ڂ`�d�a�����{���{�~���W�S���@�@�i�I�j
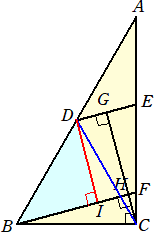
��R�i�E�j�@���}�ɂ����āA���`�a�b�́ڂ`�b�a���X�O���̒��p�O�p�`�ł���A�_�c�͕ӂ`�a��
�@�@���_�ł���B�܂��A�Q�_�d�A�e�͕ӂ`�b��̓_�ŁA�a�b���b�d�ł���A�a�e�a�c�d�ł���B
�@�@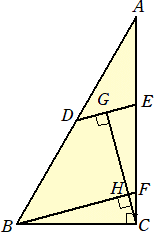
�@����ɁA�_�f�͐����c�d�̒��_�ł���A�_�g�͐����a�e�Ɛ����b�f�Ƃ̌�_�ł���B
�@�`�a���Q�S�A�a�b���P�Q�̂Ƃ��A�����f�g�̒��������߂�B
�i���j�@��ӂ��A���`�a�b�ɂ����āA�ڂ`���R�O���A�ڂ`�a�b���U�O���ł���B
�@�@
�@���̂Ƃ��A�`�c���b�c���P�Q�@�Ȃ̂ŁA�ڂc�b�d���ڂ`���R�O���ł���B
�@�b�f�͂Q���ӎO�p�`�b�c�d�ɂ����āA�ڂc�b�d�̂Q�������Ȃ̂ŁA�ڂf�b�d���P�T���ƂȂ�B
���̂Ƃ��A���a�b�e�䁢�b�g�e�@�Ȃ̂ŁA�@�ڂb�a�e���ڂg�b�e���P�T��
�@����āA�ڂc�a�h���U�O���|�P�T�����S�T���ƂȂ�̂ŁA
�@�f�g���c�h���P�Q�~�i![]() /�Q�j���U
/�Q�j���U![]() �@�@�i�I�j
�@�@�i�I�j
�i�R�����g�j�@�O�p���p����A
�@�f�g���i�P�Q![]() �|�P�Q�j�������P�T�����P�Q�i
�|�P�Q�j�������P�T�����P�Q�i![]() �|�P�j
�|�P�j![]() �i
�i![]() �{�P�j/�S���U
�{�P�j/�S���U![]()
�ƊȒP�ɋ��߂��邪�A����́A���w���ɂ͖������ȁD�D�D�H
��R�i�G�j�@�S���̐H�����R�O�O�����������r�[�J�[����A�H���� �� �������o�����B���̌�A
�@�r�[�J�[�Ɏc���Ă���H�����ɐH�� �� ���������Ă悭�����������Ƃ���A�P�Q���̐H����
�@�ɂȂ����B���̂Ƃ��A�� �̒l�����߂�B
�i���j�@��ӂ��A�@�O�D�O�S�~�i�R�O�O�|���j�{�����O�D�P�Q�~�R�O�O�@�Ȃ̂ŁA
�@�P�Q�|�O�D�O�S���{�����R�U�@���A�@�O�D�X�U�����Q�S�@�������āA�@�����Q�T�i���j�@�@�i�I�j
�i�R�����g�j�@���������H�����̔Z�x�̖��ł́A�K�Ȗ��ݒ肩�A�悭���ӂ��Ă���B�P�O�O
�@�@�@�@�@���� �̐��ɗn����H���̗ʂ́A��R�U�������E�ŁA�Z�x���ƁA��Q�U�D�T�����炢�B
��S�@���}�̂悤�ɁA������ �����i�P/�U�j��2 �ƒ��� �����|�� �A�����|�R�� ���^�����Ă���B
�@�_A�i�|�U�C�U�j�A�_B�i�U�C�U�j�A�_C�i�|�Q�C�U�j�A�_D�i�|�U�C�O�j�A�_E�i�|�U�C�R�j�Ƃ���B
�@����ɁA���_���n�Ƃ���Ƃ��A�_F�͒��� �����|�R�� ��̓_�ŁACO �F OF�� �Q �F �P �ł���A��
�� �� ���W�͐��ł���B
�@�@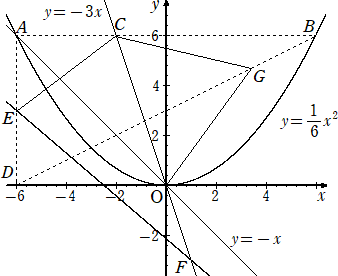
�@����BD��ɓ_G���A��CEF�Ɓ�COG�̖ʐς̔䂪 ��CEF �F ��COG���R �F �Q �ŁA���� ��
���W�����ƂȂ�悤�ɂƂ�B���̂Ƃ��́A�_G�� �� ���W�����߂�B
�i���j�@���b�d�e �F ���b�d�n���R �F �Q �Ȃ̂ŁA�@���b�d�n����COG�@�ł���B
�@�_E�i�|�U�C�R�j��ʂ�A���� �����|�R�� �ƕ��s�Ȓ����́A�@�����|�R�i���{�U�j�{�R���|�R���|�P�T
�@����āA�� ���Ɠ_�i�|�T�C�O�j�Ō����B
�@���b�d�n����COG�@�Ȃ̂ŁA�_�f��ʂ�A���� �����|�R�� �ƕ��s�Ȓ����́A�� ���Ɠ_�i�T�C�O�j
�Ō����B���̒����̎��́A�@�����|�R�i���|�T�j���|�R���{�P�T
�@�����a�c�̕������́A�@�����i�P/�Q�j���{�R�@�Ȃ̂ŁA���̌�_�����߂�ƁA
�@�|�R���{�P�T���i�P/�Q�j���{�R�@���A�@�i�V/�Q�j�����P�Q�@���Ȃ킿�A�@�����Q�S/�V�@�@�i�I�j
��T�@�P�A�Q�A�R�A�S�A�T�A�U�̐����P�������ꂽ�U���̃J�[�h������B
�@��A���Q�̂���������ɂP���A�傫����������̏o���ڂ̐��� ���A������������
�@��̏o���ڂ̐��� �� �Ƃ���B�o���ڂ̐��ɂ���āA���́y����P�z�A�y����Q�z�����ɍs���A
�@�c�����J�[�h�ɂ��čl����B
�y����P�z�@�� �̖������ꂽ�J�[�h�����ׂĎ�菜���B
�y����Q�z�@�� �������ꂽ�J�[�h����菜���B�������A�y����P�z�ɂ��A�� �������ꂽ�J�[�h��
�@�@�@�@�@���łɎ�菜���Ă����ꍇ�́A�c���Ă���J�[�h�̂����A�ł��傫�����������ꂽ
�@�@�@�@�@�J�[�h����菜���B
�@��A���Q�̂���������ɂP����Ƃ��A���̖₢�ɓ�����B�������A��A���Q�̂�
������͂Ƃ��ɁA�P����U�܂ł̂ǂ̖ڂ��o�邱�Ƃ����l�Ɋm���炵�����̂Ƃ���B
�i�A�j�@�c�����J�[�h���u�S�v�̃J�[�h�P�������ɂȂ�m�������߂�B
�i�C�j�@�c�����J�[�h�ɁA�u�U�v�̃J�[�h���܂܂��m�������߂�B
�i���j�@�c�����J�[�h�̋N���蓾��ꍇ��\�ɂ܂Ƃ߂�ƁA
| ��_�� | �P | �Q | �R | �S | �T | �U |
| �P | �Q�R�S�T | �R�S�T�U | �Q�S�T�U | �Q�R�T�U | �Q�R�S�U | �Q�R�S�T |
| �Q | �R�S�T | �R�S�T | �S�T�U | �R�T�U | �R�S�U | �R�S�T |
| �R | �Q�S�T | �S�T�U | �Q�S�T | �Q�T�U | �Q�S�U | �Q�S�T |
| �S | �R�T | �R�T | �T�U | �R�T | �R�U | �R�T |
| �T | �Q�R�S | �R�S�U | �Q�S�U | �Q�R�U | �Q�R�S | �Q�R�S |
| �U | �S | �S | �S | �T | �S | �S |
�@����āA���߂�m���́A
�i�A�j�@�T/�R�U�@�@�i�C�j�@�P�T/�R�U���T/�P�Q�@�ƂȂ�B�@�@�i�I�j
��U�@���}�́A�_A�_�Ƃ��ABC��CD �̓ӎO�p�`BCD���ʁA���`�d�a�A���`�a�c�A
�@���`�c�e�𑤖ʂƂ���O�p�����̓W�J�}�ł���A�ڂ`�d�a���ڂ`�e�c���X�O���ł���B
�@�@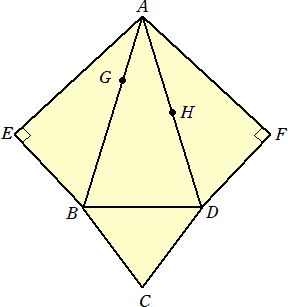
�@�܂��A�_G�͕�AB��̓_�ŁAAG �F GB���P �F �Q �ł���A�_�g�͕�AD�̒��_�ł���B
AE���P�Ocm�ABC���Tcm�ABD���Ucm �̂Ƃ��A���̓W�J�}��g�ݗ��ĂĂł���O�p�����ɂ�
���āA���̖₢�ɓ�����B
�i�C�j�@�R�_C�AE�AF ���d�Ȃ����_�� I �Ƃ���B���̎O�p�����̑��ʏ�ɁA�_G����� AI �ƌ�
�@�@���悤�ɓ_H�܂Ő��������B���̂悤�Ȑ��̂����A�ł��Z���Ȃ�悤�Ɉ��������̒�����
�@�@���߂�B
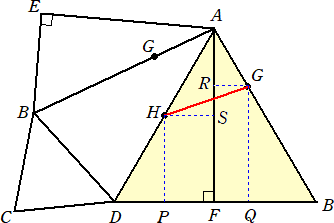
�i���j�@���}�̂悤�ɁA���ʂ`�d�a���`�e���Ɉړ������čl����B���߂�����́A���}�̐ԐF��
�@�����f�g�ł���B�f�A�g���A�����a�c�ɐ��������낵�A���̑������ꂼ��p�A�o�Ƃ����B���l
�@�ɁA�f�A�g���A�����`�e�ɐ��������낵�A���̑������ꂼ��q�A�r�Ƃ����B
�@�@
�@�f�́AAG �F GB���P �F �Q �Ȃ̂ŁA�e�a���T���A�e�p���T/�R�@�ŁA����ɁA�`�e���P�O���A
�q�e���Q�O/�R
�@�g�́A��AD�̒��_�Ȃ̂ŁA�e�c���T���A�@�o�e���T/�Q�@�ŁA����ɁA�`�e���P�O���A�r�e���T
�@����āA�@�f�g2���i�T/�Q�{�T/�R�j2�{�i�Q�O/�R�|�T�j2���U�Q�T/�R�U�{�Q�T/�X���V�Q�T/�R�U�@���A
�@�f�g���i�T/�U�j![]() �@�@�i�I�j
�@�@�i�I�j
�i�ʉ��j�@�����f�a�̒��_���l�Ƃ��A�l��������e�a�ɐ����l�m�������B
�@�@
�@���`�c�l�ɂ����āA���_�A���藝���A�@�f�g���i�P/�Q�j�c�l
�����ŁA�@�c�l2���i�T�{�P�O/�R�j2�{�i�P�O/�R�j2���U�Q�T/�X�{�P�O�O/�X���V�Q�T/�X�@���A
�@�c�l���i�T/�R�j![]() �@�Ȃ̂ŁA�@�f�g���i�T/�U�j
�@�Ȃ̂ŁA�@�f�g���i�T/�U�j![]() �@�@�i�I�j
�@�@�i�I�j
�i�R�����g�j�@��N�Ɣ�ׂāA��背�x���͕��Ղ������悤�Ɋ����܂����B���ϓ_����オ��
�@�@�@�@�@���ȁH
�i�NjL�j�@�ߘa�V�N�Q���P�T���t��
�@�ߘa�V�N�Q���P�S���i���j�ɍs��ꂽ�_�ސ쌧�������Z�����̖�肪�����̐V��������
�f�ڂ��ꂽ�B���������������������������Ă݂����Ǝv���B���ɂ���Ă͉��肳���
����B
��R�@�@���̖₢�ɓ�����B
(�A)�@���}�̂悤�ɁA����AB�a�Ƃ���~O�̎���ɂQ�_A�AB�Ƃ͈قȂ�_C���AAC��BC
�@�ƂȂ�悤�ɂƂ�B�܂��A�~O�̎���ɓ_D���A��CAD���݊p�ƂȂ�悤�ɂƂ�A����AB�Ɛ�
�@��CD�Ƃ̌�_��E�Ƃ���B����ɁA����CB�̉�����ɓ_F���ACF��DF�ƂȂ�悤�ɂƂ�A��
�@��DF�Ɖ~O�Ƃ̌�_��G�A����AG�Ɛ���BD�Ƃ̌�_��H�Ƃ���B
�@�@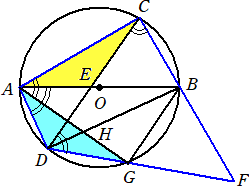
�@���̂Ƃ��A���́i�@�j�i�A�j�ɓ�����B
�i�@�j�@��ACE�䁢AGD�ł��邱�Əؖ�����B
�i�A�j�@BC���Scm�ABG��FG���Qcm �̂Ƃ��A��ADH�̖ʐς����߂�B
�i���j�i�@�j�@��ACE�Ɓ�AGD�ɂ����āA��AD�ɑ���~���p����A��ACE����AGD
�@FC��FD�@���A��FCD����FDC
�@��BD�ɑ���~���p����A�@��BCD����BAD
�@��CG�ɑ���~���p����A�@��CDG����CAG
�@����āA�@��BAD����CAG�@�ƂȂ�̂ŁA�@��CAE����GAD
�ȏォ��A�Ή�����Q�p���������̂ŁA�@��ACE�䁢AGD�ł���B
�i�A�j�@�b�c�a�a�f ���A���e�a�f�͂Q���ӎO�p�`�Ȃ̂ŁA�a�e���Q�A�c�f���S
�@���̂Ƃ��A���e�a�f�͐��O�p�`�ŁA�ڂa�b�c���U�O���@�ŁA��BAD���U�O��
��ADB���X�O���@���AAD�����@�Ƃ����ƁA�@AB���Q���@�ABD��![]() ���@�ł���B
���@�ł���B
�@�O�����̒藝���A�@BD2���P2�{�i�R![]() �j2���Q�W���i
�j2���Q�W���i![]() ���j2�@�Ȃ̂ŁA�@�Q
���j2�@�Ȃ̂ŁA�@�Q![]() ��
��![]() ��
��
����āA�@�����Q![]() /
/![]()
���̂Ƃ��AAC2���i�S![]() /
/![]() �j2�|�P�U���U�S/�R�@���A�@AC���W/
�j2�|�P�U���U�S/�R�@���A�@AC���W/![]()
�܂��A�@��ADH�䁢ACB�@�ŁA��ACB���S�E�i�W/![]() �j�E�i�P/�Q�j���P�U/
�j�E�i�P/�Q�j���P�U/![]()
������́A�@�� �F �W/![]() ���Q
���Q![]() /
/![]() �F �W/
�F �W/![]() ��
��![]() �F �S�@�Ȃ̂ŁA
�F �S�@�Ȃ̂ŁA
���߂�ʐς́A�@��ADH���P�U/![]() �E�i
�E�i![]() /�S�j2���V/
/�S�j2���V/![]() �@�@�i�I�j
�@�@�i�I�j
�@���̂悤�ȕʉ����l������B
�@�@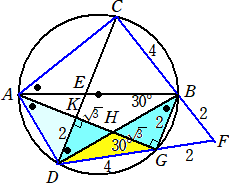
�i�i�A�j�̕ʉ��j�@�b�c�a�a�f ���A���e�a�f�͂Q���ӎO�p�`�Ȃ̂ŁA�a�e���Q�A�c�f���S
�@���̂Ƃ��A���e�a�f�͐��O�p�`�ŁA�ڂe�b�c���ڂe�c�b����BAD���U�O���@�ł���B
�@��ADB���X�O���A��ABD���R�O���@���A�@��AGD���R�O��
�@��AGB���X�O���ŁA�b�c�a�a�f ���A��GKD���X�O��
����āA�ڂj�c�b���U�O���ŁA�c�f���S�@����A�j�c���Q�A�j�f���Q![]()
���g�j�c�߁��g�f�a�@���A�@�g�j���g�f��![]() �@�Ȃ̂ŁA�c�g��
�@�Ȃ̂ŁA�c�g��![]() �@�ƂȂ�B
�@�ƂȂ�B
���̂Ƃ��A�@�a�c���Q![]() �@����A�@AD���Q
�@����A�@AD���Q![]() /
/![]()
���������āA�@��ADH��![]() �E�i�Q
�E�i�Q![]() /
/![]() �j�E�i�P/�Q�j���V/
�j�E�i�P/�Q�j���V/![]() �@�@�i�I�j
�@�@�i�I�j
�i�R�����g�j�@�����ƊȒP�ɋ��߂��Ȃ����ȁH
�i�G�j�@���}�ɂ����āA�l�p�`ABCD�͐����`�ł���A��ADE�́A��ADE���Q�V���A��AED���X�O��
�@�@�̒��p�O�p�`�ł���B�܂��A�_F�͐���DE��̓_�ŁAAE�aBF�ł���A�_G�͐���AC�Ɛ���
�@�@BF�Ƃ̌�_�ł���B���̂Ƃ��A��CGD�̑傫�������߂�
�@�@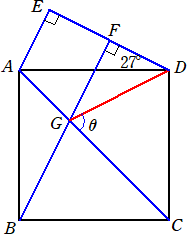
�i���j�@��EAD���U�R���ŁA�ڂf�a�b���U�R���@���A�@��ABG���Q�V��
��BAG���S�T���@���A�@��AGB���P�W�O���|�S�T���|�Q�V�����P�O�W��
��ABG�߁�ADG�@���A�@��AG�a����AGD���P�O�W��
����āA�@�Ɓ��P�W�O���|�P�O�W�����V�Q���@�@�i�I�j
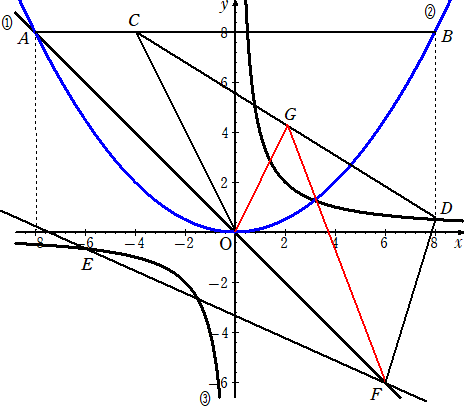
��S�@�@���}�ɂ����āA�����@�Fy���|x �ŁA�Ȑ��A�F��������2 �A�Ȑ��B�F�����S/�� �ł���B�_A��
�@�@�����@�ƋȐ��A�Ƃ̌�_�ŁA���� �� ���W�́|�W�ł���B�_B�͋Ȑ��A��̓_�ŁA����AB
�@�@�� �� ���ɕ��s�ł���B�_C�͐���AB��̓_�ŁAAC�FCB���P�F�R �ł���B�܂��A�_D�͋Ȑ�
�@�@�B��̓_�ŁA����BD�� �� ���ɕ��s�ł���B�_E�͋Ȑ��B��̓_�ŁA���� �� ���W�́|�U��
�@�@����B����ɁA���_��O�Ƃ���Ƃ��A�_F�͒����@��̓_�ŁAAO�FOF���S�F�R�ŁA���� �� ���W
�@�@�͐��ł���B
�@�@
�@���̂Ƃ��A���̖₢�ɓ�����B
�i�C�j�@�Ȑ��A�̎������߂�B
�i���j�@����EF�̎������߂�B
�i�n�j�@����CD��ɓ_G��CG��GD�ƂȂ�悤�ɂƂ�B���̂Ƃ��́A��COG�Ɓ�DGF�̖ʐϔ��
�@�@�ł��ȒP�Ȑ����̔�ŕ\���B
�i���j�i�C�j�@�`�i�|�W�C�W�j��ʂ邩��A�@�U�S�����W�@���A�@�����P/�W
�i���j�@�d�i�|�U�C�|�Q/�R�j�A�e�i�U�C�|�U�j�@��ʂ�̂ŁA
�@�����i�|�U�{�Q/�R�j/�i�U�{�U�j�E�i���|�U�j�|�U���|�i�S/�X�j���|�P�O/�R
�i�n�j�@�b�i�|�S�C�W�j�A�c�i�W�C�P/�Q�j�@�Ȃ̂ŁA�����b�c�́A
�@�����i�P/�Q�|�W�j/�i�W�{�S�j�E�i���{�S�j�{�W���|�i�T/�W�j���{�P�P/�Q
�@���̒����b�c�́A�g�i�O�C�P�P/�Q�j�A�j�i�U�C�V/�S�j�@��ʂ�B
�@�b�f���f�c�@�Ȃ̂ŁA�@��COG �F ��DGF��OH �F �e�j���P�P/�Q �F �R�P/�S���Q�Q �F �R�P�@�@�i�I�j
��T�@�@�R�O���̂����肪�W�A�T�O���̂����肪�V�A�W�O���̂����肪�P����B�召�Q�̂���
�@�@������ɂP���A�傫����������̏o���ڂ̐��� ���A��������������̏o���ڂ̐�
�@�@�� �� �Ƃ���B
�@��������̏o���ڂ̐��ɂ���āAK�����L����́A���́y���[���z�ɂ��������āA�����̂�
�������蕪����B���ꂼ�ꂪ���������������ׂĂ͂���ɂ̂��A�v�������d���ɂ���
�l����B
�y���[���z�@�܂��AK����͂R�O���̂������ �� �ƂT�O���̂������ �� ���AL����͎c����
�@�@�R�O���̂�����ƂT�O���̂���������ׂĎ��B���ɁAK�����L����̂����A�R�O���̂������
�@�@�T�O���̂���������킹�����̏��Ȃ������W�O���̂���������B
�@���܁A�召�Q�̂���������ɂP����Ƃ��A���̖₢�ɓ�����B�������A�召�Q��
�̂�������͂Ƃ��� �P����U�܂ł̂ǂ̖ڂ��o�邱�Ƃ����l�Ɋm���炵�����̂Ƃ���B
(�C)�@K����̌v�������d�����Q�O�O�������ƂȂ�m�������߂�B
(��)�@K����̌v�������d����L����̌v�������d�����d���Ȃ�m�������߂�B
�i���j�@�j�����d����\�ɂ܂Ƃ߂�ƁA
| ���_�� | �P | �Q | �R | �S | �T | �U |
| �P | �P�U�O | �Q�P�O | �Q�U�O | �R�P�O | �R�U�O | �S�P�O |
| 2 | �P�X�O | �Q�S�O | �Q�X�O | �R�S�O | �R�X�O | �R�U�O |
| �R | �Q�Q�O | �Q�V�O | �R�Q�O | �R�V�O | �R�S�O | �R�X�O |
| 4 | �Q�T�O | �R�O�O | �R�T�O | �R�Q�O | �R�V�O | �S�Q�O |
| �T | �Q�W�O | �R�R�O | �R�O�O | �R�T�O | �S�O�O | �S�T�O |
| �U | �R�P�O | �Q�W�O | �R�R�O | �R�W�O | �S�R�O | �S�W�O |
�i�C�j�@�\���A���߂�m���́A�@�Q/�R�U���P/�P�W
�i���j�@�d���̍��v���U�V�O���Ȃ̂ŁAK����̌v�������d����L����̌v�������d�����d���Ȃ�
�@�̂́A�R�R�T���ȏ�B����āA�\���A���߂�m���́A�@�P�V/�R�U�@�@�i�I�j
�i�R�����g�j�@�\�����̂����\��ςł����I
��U�@�@���}�́AAB��BC���P�R�icm�j�AAC���P�O�icm�j�̓ӎO�p�`ABC���ʂƂ��A
�@�@AD��BE��CF���P�W�icm�j�������Ƃ���O�p���ł���B
�@�܂��A�_G�͕�BE��̓_�ŁABG �F GE���W �F �P�ł���A�_�g�͕�BE�̒��_�ł���B
�@�@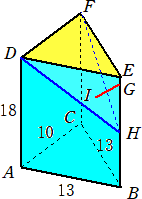
�@���̂Ƃ��A���̖₢�ɓ�����B
�i�C�j�@���̎O�p���̕\�ʐς����߂�B
�i���j�@���̎O�p���ɂ����āA�}�̂悤�ɁA�_G����R�_D�AF�AH��ʂ镽�ʂɈ����������ƂR�_D�AF�A�g��ʂ镽
�@�@�ʂƂ̌�_�� I �Ƃ���B���̂Ƃ��̐��� GI �̒��������߂�B
�i���j�i�C�j�@�P�R�E�P�W�E�Q�{�P�O�E�P�W�{�P�O�E�P�Q�E�i�P/�Q�j�E�Q���V�U�W�i����2�j
�i���j�@�g�c���g�e���T![]() �@�Ȃ̂ŁA�e�c���ӂƂ��遢�gFD�̍����́A�P�T����
�@�Ȃ̂ŁA�e�c���ӂƂ��遢�gFD�̍����́A�P�T����
�@����āA���g�e�c���P�O�E�P�T�E�i�P/�Q�j���V�T�i����2�j
�@�����ŁA�O�p���g-EFD�̑̐ς́A�@�P�O�E�P�Q�E�i�P/�Q�j�E�X�E�i�P/�R�j���P�W�O�i����3�j
�@�d���灢�g�e�c�ɉ����������̑����j�Ƃ���ƁA�@�V�T�EEK�E�i�P/�R�j���P�W�O�@���AEK���R�U/�T
�@����āA�@�f�h���i�R�U/�T�j�E�i�V/�X�j���Q�W/�T�i�����j�@�@�i�I�j
�@�@�ȉ��A�H�����I
�@�@�@�@�@�@�@�@�@�@�@�@�@�@