的に、どの角に来るか?但し、反射の法則に従うものとする。
1.
M=奇数、N=奇数ならば、座標(M、N)
M=偶数、N=奇数ならば、座標(0,M)
M=奇数、N=偶数ならば、座標(N、0)
M=偶数、N=偶数ならば、公約数で割って考える。
と、方向性が分かる。
座標の和が、偶数のところしか通らないのでわかります。
2. 何回反射するか?
公倍数から2をひくとよさそうですが、説明が出来てません。
跳ね返りの回数は、最小公倍数をLとして、 L/M+L/N−2 でした。
らすかるさんからのコメントです。(令和2年4月25日付け)
反射のかわりに、進む先に反転した図を書いていくという、よくある方法を使えばわかると
思います。
角に到達するためには、MとNの最小公倍数進む必要があります。
最大公約数を g とすると、縦横に MN/g 進んだところで角に到達し、このとき、横に進ん
だ距離 MN/g は、横幅 N の M/g 倍なので、左右の壁に反射した回数は、M/g−1、縦に
進んだ距離 MN/g は、縦幅 M の N/g 倍なので、上下の壁に反射した回数は、N/g−1
よって、(M/g−1)+(N/g−1)=(M+N)/g−2回反射します。
(コメント) らすかるさんの考え方を作図してみました。
例えば、縦M=2、横N=3とすると、
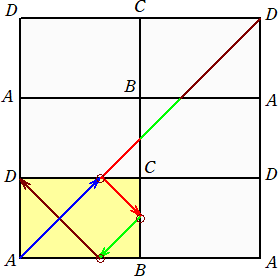
傾き1でAを出発した玉は、3回反射して、Dに到達することが分かる。
ksさんからのコメントです。(令和2年4月25日付け)
有難うございます。前にも似た質問があったようで恐縮です。
3.いくつの格子を通るか=最小公倍数 も言えますね。
(参考) 「光の到達」
ksさんからのコメントです。(令和2年4月28日付け)
問題を発展的に、傾きを b/a にしたとき、横をbに細分し、縦をaに細分し、格子を正方形
にのばせば、傾き1の場合に還元されますね。
1.角、2.はね返り回数、3.通過する格子数 がわかる。
