んで作れるのは、一組しかないみたいですね。
(コメント) 「魔方陣の話題」によれば、3×3の魔方陣は、回転と裏返しを同一視すると、
1種類しかないが...。でもタイトルが、「平方数」の方陣。どんな意味なんだろう?
ksさんからのコメントです。(令和2年4月16日付け)
1と9、25と36、784を並べる組しかないという意味です。
カルピスさんからのコメントです。(令和2年4月17日付け)
これは、1〜9までの数字を使って出来る平方数は沢山あるが、1〜9の「全て」を使い、
かつ 「1回だけ」使うという条件にすると、この5個だけで1通りという意味でしょうか?
とすると、はて?「方陣」との関係が??
たまたま、3×3の方陣を眺めていた時、ふと、全てを「平方数」にしてみたくなったとか・・・。
カルピスさんからのコメントです。(令和2年4月18日付け)
上記の投稿、大変失礼いたしました。「魔方陣」ではなく『方陣』でしたね。縦・横・斜め の
合計が同じとか、全く関係なかったのですよね。思い込みって、怖い・・・。
(コメント) 1=12、9=32、25=52、36=62、784=282 なんですね!
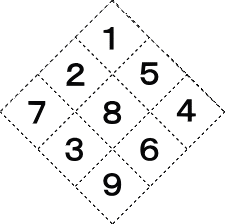
方陣を作ってみました。
GAIさんからのコメントです。(令和2年4月19日付け)
冒頭の問題を、一桁を2個、二桁を2個、三桁を1個の素数を用いて、3×3の方陣を斜めに
して、これらを配置すると、1〜9の数字が一つずつ含まれる計5個の素数を探す問題にして
も楽しめますね。
さて、このような5個の素数の組み合わせは何組あるでしょう?
DD++さんからのコメントです。(令和2年4月19日付け)
ksさんのコメントを見て、「へー、平方数の中に、7って 24^2=576 まで出てこないんだ」と
感心したところでふと思った疑問。
平方数を小さい順にひたすら書いていったとき、各数字の登場頻度順位ってどうなるんで
しょう?
十分大きな数まで調査したら、1、4、6、9、5、2、3、0、7、8 の順になるのかなという気がし
ますが、実際のところどうなんでしょうか?
GAIさんからのコメントです。(令和2年4月19日付け)
上から、n=1〜10^k (k=1,2,3,・・・,7)での、n^2に含まれる 0〜9 の数字の頻度分布になりま
す。[左端が0,右端が9です。]
n=1〜10^1のときの頻度分布
%222 = [2, 4, 1, 1, 3, 1, 3, 0, 1, 2]
n=1〜10^2のときの頻度分布
%223 = [40, 48, 44, 21, 50, 27, 48, 19, 24, 37]
n=1〜10^3のときの頻度分布
%224 = [617, 681, 655, 386, 700, 468, 694, 344, 442, 556]
n=1〜10^4のときの頻度分布
%225 = [8385, 8731, 8660, 5812, 8938, 6737, 8932, 5354, 6365, 7468]
n=1〜10^5のときの頻度分布
%226 = [104673, 107246, 106719, 77971, 109268, 87413, 109260, 73410, 83587, 94214]
n=1〜10^6のときの頻度分布
%227 = [1249004, 1271895, 1268018, 979247, 1291961, 1074677,
1292735, 933217, 1035346, 1141435]
n=1〜10^7のときの頻度分布
%228 = [14498558, 14716810, 14682568, 11790761,
14917636, 12746727, 14928221, 11330094, 12352149, 13411735]
DD++さんからのコメントです。(令和2年4月19日付け)
なるほど、(10^7)^2 までだと、6、4、1、2、0、9、5、8、3、7 の順なんですね。
先頭位の数字に出やすい「1」よりも「4」や「6」が多い理由ってなんなんでしょうね。あと、一
の位に絶対出てこない「2」がなぜこんなにも多いのか……。
GAIさんからのコメントです。(令和2年4月19日付け)
ちなみに、立方数での n=1〜10^7 までのn^3に現れる数の統計を見てみたら、
%236 = [21042287, 21298184, 20894124, 20247733, 19762202,
19603084, 19746312, 19946829, 19565039, 19231974]
で、数字での現れる順番でみると、 [1>0>2>3>7>4>6>5>8>9] になるようです。
らすかるさんからのコメントです。(令和2年4月19日付け)
もっと大きい数までだと変わるかもと思って、(10^8)^2までと(10^9)^2までを計算して見まし
た。
(10^8)^2まで
165007949, 167170698, 166829770, 137901007, 169168564,
147472302, 169283924, 133290566, 143519263, 154108441
(10^9)^2まで
1850153770, 1871692967, 1868319143, 1578989488, 1891670644,
1674734804, 1892844584, 1532875244, 1635186153, 1741057922
順位は、6,4,1,2,0,9,5,8,3,7 のまま変わらないですね。
「1」よりも「4」や「6」が多い理由は、下位桁による影響だと思います。
2桁の00〜99の2乗の下位2桁は、 34, 24, 22, 4, 32, 14, 32, 4, 12, 24
3桁の000〜999の2乗の下位3桁は、 461, 332, 348, 112, 428, 222, 448, 112, 208, 332
4桁の0000〜9999の2乗の下位4桁は、
5792, 4232, 4588, 2032, 5288, 3232, 5488, 2032, 3088, 4232
5桁の00000〜99999の2乗の下位5桁は、
68481, 52124, 56176, 30024, 62876, 42324, 65076, 30024, 40776, 52124
6桁の000000〜999999の2乗の下位6桁は、
786962, 620444, 662956, 399444, 728456, 523444, 750956, 399444, 507956, 619944
なので、下位2桁だけ違いますが、それ以外では、 0,6,4,2,1,9,5,8,3,7 の順となっています。
(ただし3と7は同順位、また5桁以下では1と9は同順位)
「0」が多いですが、「0」はゼロサプレスで大きく減りますので順位を落とし、あとは先頭桁
で「1」が多いことで、「1」が順位を1つ上げている、ということでしょう。
下位桁でこれだけ差があることを考えると、上限をいくら増やしても、6,4,1,2,0,9,5,8,3,7 とい
う順位は変わらない可能性がありますね。
