CFが1点Pで交わるものとする。
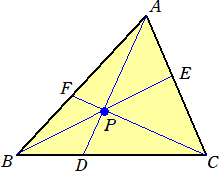 このとき、
このとき、が成り立つことを示せ。
(証明) 底辺が等しい2つの三角形の面積の比は高さの比に等しいので、
PD/AD=△PBC/△ABC 、PE/BE=△PCA/△ABC 、PF/CF=△PAB/△ABC
よって、
PD/AD+PE/BE+PF/CF=(△PBC+△PCA+△PAB)/△ABC=1 (終)
(コメント) 位置ベクトルを用いて、A(a)、B(b)、C(c)、P(p) とすると、
p=(PD/AD)a+(PE/BE)b+(PF/CF)c
が成り立つ。このとき、
という条件は、点Pが3点A、B、Cの張る平面上にあることを示す。
ところで、 p=(PD/AD)a+(PE/BE)b+(PF/CF)c が成り立つことは次のように示
される。
(証明) △PBC=x、△PCA=y、△PAB=z とおくと、
BD:DC=z:y 、CE:EA=x:z 、AF:FB=y:x が成り立つ。
このとき、
AP=[(y+z)/(x+y+z)]AD=[(y+z)/(x+y+z)][(yAB+zAC)/(y+z)]
=(yAB+zAC)/(x+y+z)
より、 p=[x/(x+y+z)]a+[y/(x+y+z)]b+[z/(x+y+z)]c
ここで、 x/(x+y+z)=△PBC/△ABC=PD/AD
同様にして、 y/(x+y+z)=△PCA/△ABC=PE/BE
z/(x+y+z)=△PAB/△ABC=PF/CF
なので、 p=(PD/AD)a+(PE/BE)b+(PF/CF)c が成り立つ。 (証終)
りらひいさんからのコメントです。(令和元年12月3日付け)
メネラウスの定理より、
PE/EB * BC/CD * DA/AP = 1 、PF/FC * CB/BD * DA/AP = 1 が成り立つので、
PE/BE + PF/CF
= CD/BC * AP/AD + BD/CB * AP/AD
= (DC+BD)/BC * AP/AD
= BC/BC * (AD-PD)/AD
= 1 * (AD/AD - PD/AD)
= 1 - PD/AD
より、 PD/AD + PE/BE + PF/CF = 1
(コメント) 直線が三角形と交わらない場合にメネラウスの定理を適用するのはあまり経験
がなかったので、勉強になりました。(→ 参考:「メネラウスの定理」)
