Q、Rとする。そして、3つの線分AQ、BR、CPを引けば中にこの3本の直線で囲まれる三角
形が出現する。(ただし、P、Q、Rは同時に各辺の中点となることはないものとする。)
このとき、中に出現した三角形の面積が元の△ABCの面積のちょうど半分になるようにす
るには、内分点P、Q、Rを如何なる取り方をしておけばよいか?
らすかるさんからのコメントです。(令和元年10月30日付け)
(ただし、P、Q、Rは同時に各辺の中点となることはないものとする。)
これは、三角形が出来ない場合を除いているものと思いますが、三角形が出来ない場合
は他にもありますね。
GAIさんからのコメントです。(令和元年10月30日付け)
あーそうですね。なんか勘違いしていました。とにかく ”一点では交わらない3本の直線に
おいて” の条件で考察願います。
(コメント) 「分割パズル(10)」のラウスの定理を用いると、解決の糸口がありそうと思って
計算してみました。
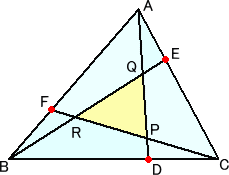
面積1の△ABCにおいて、BD:DC=1:x、CE:EA=1:y、AF:FB=1:z とすると、
△PQR=(xyz−1)2/{(xy+y+1)(yz+z+1)(zx+x+1)}
なので、(xyz−1)2/{(xy+y+1)(yz+z+1)(zx+x+1)}=1/2 となるような x、y、z を
探せばよい。
x=1/2、y=1/3、z=1/4 のとき、
(xyz−1)2/{(xy+y+1)(yz+z+1)(zx+x+1)}=529/1872=0.28258547・・・
x=1/3、y=1/6、z=1/7 のとき、
(xyz−1)2/{(xy+y+1)(yz+z+1)(zx+x+1)}=529/1872=0.48076923・・・
x=1/3、y=1/5、z=1/9 のとき、
(xyz−1)2/{(xy+y+1)(yz+z+1)(zx+x+1)}=0.500822804・・・
x=1/3、y=1/6、z=1/7 のとき、
(xyz−1)2/{(xy+y+1)(yz+z+1)(zx+x+1)}=0.499808073・・・
#ピッタリ0.5となるのを探すのは、なかなか難しい...。
スモークマンさんからのコメントです。(令和元年10月31日付け)
以前、以下のサイトで考えた一般式から...
水の流れ No 367回の問題の解答より:
AP:PB=m:n として、 △PQR/△ABC=(m-n)^2/(m^2+mn+n^2)=1/2
m^2+mn+n^2=2(m-n)^2 より、 m^2-5mn+n^2=0 を満たしていればいいはずですね ^^
GAIさんからのコメントです。(令和元年11月1日付け)
スモークマンさんのものは、点P、Q、Rの取り方を共通の内分点として選択した場合の考
察になっているものと思われますが、ここでは、P、Q、Rはそれぞれ自由に独立して内分点
が選べます。
らすかるさんからのコメントです。(令和元年11月1日付け)
GAIさんのコメントを見て、「そういえばスモークマンさんが出した方程式に解はあるのか?」
と思ったので、スモークマンさん提示の m^2-5mn+n^2=0 の解を考えたのですが、mについて
解くと m=(5±√21)n/2 となることから、明らかに自然数解はありませんでした。
スモークマンさんからのコメントです。(令和元年11月1日付け)
あら...^^; またしても独り合点して、掲示板を汚してしまいました...〜m(_ _);m〜
らすかるさんからのコメントです。(令和元年11月1日付け)
上記(コメント)のラウスの定理による式
(xyz-1)^2/{(xy+y+1)(yz+z+1)(zx+x+1)}=1/2
を、xについて整理すると、
(y^2z^2-y^2z-yz^2-2yz-y)x^2-(y^2z^2+2y^2z+2yz^2+z^2+8yz+2y+2z+1)x-(y^2z+2yz+y+z-1)=0
となり、このxに関する二次方程式の判別式は、D=(yz+8y+z+1)(yz+z+1)^3 となりますので、
yz+z+1とyz+8y+z+1がともに有理数の平方であればよい(十分条件)ことがわかります。
yz+z+1=a^2、yz+8y+z+1=b^2 とおくと(ただし、a、bは有理数で、b>a>1)、
y=(b^2-a^2)/8, z=8(a^2-1)/(b^2-a^2+8)
そして、これをxの方程式に代入して解くと、
x={(a^2-4-ab)(b^2-a^2+8)}/{(b-a)(3a^3-4a^2b+ab^2+4a+4b)}、
{(4-a^2-ab)(b^2-a^2+8)}/{(b+a)(3a^3+4a^2b+ab^2+4a-4b)}
となりますので、この式から適解になるようなa、bの範囲を考えることで、
1<a<√2 かつ a<b<(4-a^2)/a として、
x=(4-a^2-ab)(b^2-a^2+8)/{(b+a)(3a^3+4a^2b+ab^2+4a-4b)}
y=(b^2-a^2)/8, z=8(a^2-1)/(b^2-a^2+8)
とすれば、元の式を満たします。
例えば、(a,b)=(5/4,7/4)とすると、(x,y,z)=(19/447,3/16,9/19)なので、
AP:PB=447:19、BQ:QC=16:3、CR:RA=19:9
で面積が半分という条件を満たすことになります。
GAIさんからのコメントです。(令和元年11月1日付け)
ラウスの定理による式 S(x,y,z)= (xyz-1)^2/{(xy+y+1)(yz+z+1)(zx+x+1) に、x、y、zの色々
な整数を代入して結果を見ていたら、x=3、y=6、z=7でピタリ1/2が起きた。
(AP:PB=1:3, BQ:QC=1:6, CR:RA=1:7に対応する。)
それ以外は結構ややこしい分数が多く、スッキリの分数として際立っていた。
余談:クライン著の「19世紀の数学」の本を2週間前ほどに読んでいたら、このラウスという
人物の人となりが書かれていて、ちょっと面白いと思って調べていたら、この人はケン
ブリッジ大学でジェイムズ・クラーク・マックスウェルと同級生らしく、マックスウェルは卒
業試験で召使に結果を見に行ってもらい、自分がトップであると確信していたために、
「二位は誰か?」と尋ねると、召使は「あなた様でございます」と答えたという逸話が残
る。そのときのトップがこのエドワ−ド・ラウスであるという。そして、彼の発見になるこ
の定理も同時にメモしていた。それが近ごろのこのサイトでの更新履歴10月30日での
分割パズル(10)を読んでいたら、まさしくこの定理が書かれているではないか!と思
いがけもなく出会ったので、これで遊んでいて、思い付いた問題でした。
他にも下記のようなパターンもあるとは思ってもいませんでした。
例えば(a,b)=(5/4,7/4)とすると(x,y,z)=(19/447,3/16,9/19)なので、
AP:PB=447:19, BQ:QC=16:3, CR:RA=19:9
で面積が半分という条件を満たすことになります。
GAIさんからのコメントです。(令和元年11月2日付け)
ラウスの定理の式: S(x,y,z)= (xyz-1)^2/{(xy+y+1)(yz+z+1)(zx+x+1)} は、中にできる三角
形の向きを念頭におけば、x、y、zの大きさが1より小や大に関わらず(分数も含め)、
S(x,y,z)=S(1/x,1/z,1/y)=S(1/z,1/y,1/x)=S(1/y,1/x,1/z)
なる関係式で処理して構わないと考えておいていいんでしょうか?
らすかるさんからのコメントです。(令和元年11月2日付け)
Pari/GPで調べると、次のようになるので大丈夫だと思います。
(16:26) gp > S(x,y,z)=(x*y*z-1)^2/((x*y+y+1)*(y*z+z+1)*(z*x+x+1))
(16:27) gp > S(x,y,z)-S(1/x,1/z,1/y)
%1 = 0
(16:27) gp > S(x,y,z)-S(1/z,1/y,1/x)
%2 = 0
(16:27) gp > S(x,y,z)-S(1/y,1/x,1/z)
%3 = 0
(16:27) gp > S(x,y,z)-S(y,z,x)
%4 = 0
(16:27) gp > S(x,y,z)-S(z,x,y)
%5 = 0
以下、工事中!
