図形の分割パズルを3題用意しました。
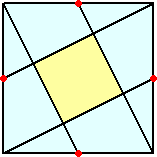
問題1 面積1の正方形から、面積が1/5の正方形を作れ。
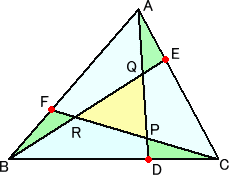
問題2 面積1の三角形から、面積が1/7の三角形を作れ。
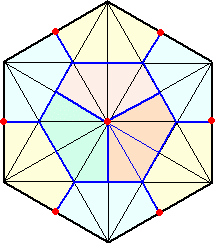
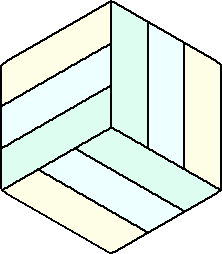
問題3 正六角形を9つの合同図形に分割せよ。
(答) 答えは、絵とにらめっこすると分かるかな?
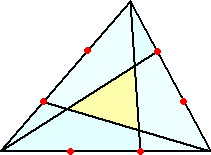
問題1の答え:頂点と中点を結ぶと、真ん中に求める正方形ができる。
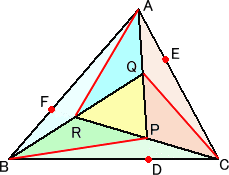
問題2の答え:三角形の3辺を2:1に分ける点を結ぶと真ん中に求める三角形ができる。
カルピスさんからのコメントです。(令和元年8月17日付け)
問題2の解き方が分かりません。教えてください。
らすかるさんからのコメントです。(令和元年8月17日付け)
△ABCでAB、BC、CAをそれぞれ2:1に内分する点をF、D、Eとし、ADとBE、BEとCF、CFと
ADの交点を順にP、Q、Rとします。
Eを通り、ADと平行な直線とBCとの交点をGとすると、DG:GC=1:2、また、BD:DC=2:1で
すから、BP:PE=BD:DG=6:1 となります。
従って、 △APE=(1/7)△ABE=(1/21)△ABC であり、△BQF、△CRDも全く同様に
(1/21)△ABCとなります。
従って、
△PQR=△ABC-△ABP-△BCQ-△CAR
=△ABC-(△ABE-△APE)-(△BCF-△BQF)-(△CAD-△CRD)
=△ABC-(△ABE+△BCF+△CAD)+(△APE+△BQF+△CRD)
=△ABC-{(1/3)△ABC+(1/3)△ABC+(1/3)△ABC}+{(1/21)△ABC+(1/21)△ABC+(1/21)△ABC}
=(1/7)△ABC
となります。
カルピスさんからのコメントです。(令和元年8月18日付け)
らすかるさん、有難うございました。やーーーーーっと理解できました。ふー、こんなに難し
いとは思いませんでした。3つの角に出来たプロペラみたいな形は、全て面積が同じで、そ
の合計が真ん中の三角形の面積になるのですね。これは、どんな三角形でも成り立つです
ね?
らすかるさんからのコメントです。(令和元年8月18日付け)
三角形ということ以外何も仮定していませんので、どんな三角形でも成り立つことになりま
すね。
(コメント) らすかるさんの証明と同様ですが、メネラウスの定理から、BP:PE=6:1 を導い
てもOKと思います。
カルピスさんからのコメントです。(令和元年8月18日付け)
らすかるさん、有難うございました。この問題2の証明は難しいので、このような条件の時
は1/7になると覚えてしまった方が良いかもですね。
(コメント) 視覚的に1/7と分かる別解を考えてみました。(令和元年8月25日付け)
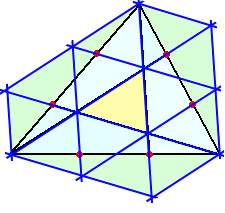
真ん中の三角形の各辺に平行な直線を描き、真ん中の三角形に合同な13個の三角形
で、元の三角形を被覆すると、面積は13(ただし、真ん中の三角形の面積=1とする。)
このとき、元の三角形の面積は、 (4÷2)×3+1=7 なので、真ん中の三角形の面積
は元の三角形の1/7となる。
(追記) 令和元年9月29日付け
問題2を一般化したものとして、ラウスの定理が知られている。
ラウスの定理 面積1の△ABCにおいて、BD=a、CD=ax、CE=b、EA=by、AF=c、
FB=cz とおくと、
△PQR=(xyz−1)2/{(xy+y+1)(yz+z+1)(zx+x+1)}
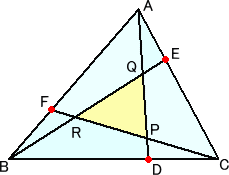
(証明) △ABDと直線FCについて、メネラウスの定理より、
(c/cz)((x+1)a/(ax))(DP/PA)=1
よって、 DP/PA=zx/(x+1)
このとき、
△APC=(x+1)/(zx+x+1)・△ADC=(x+1)/(zx+x+1)・x/(x+1)=x/(zx+x+1)
同様にして、 △BQA=y/(xy+y+1) 、△CRB=z/(yz+z+1)
よって、 △PQR=1−x/(zx+x+1)−y/(xy+y+1)−z/(yz+z+1)
地道に通分して(意外と大変な計算でした...。)
△PQR=(xyz−1)2/{(xy+y+1)(yz+z+1)(zx+x+1)} (証終)
(コメント) 問題2は、x=y=z=1/2 の場合で、実際に代入してみると、
△PQR=(1/8−1)2/(1/4+1/2+1)3=(49/64)/(49・7/64)=1/7
(追記) 令和元年10月17日付け
ラウスの定理に関連して、次の事実も興味深い。
△ABCの各辺を3等分して各辺2:1に分けてから3本の直線を引くと、互いに等し
い長さの2本の線分とそうでない線分に分かれる。
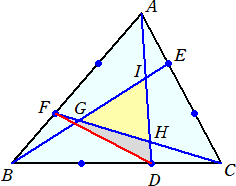
(証明) △ABC=S とおくと、 △ACF=2S/3
△CBF=S/3=△CDF+△DBF と分割すると、 △CDF=S/9、△DBF=2S/9
△ACF:△CDF=2S/3:S/9=6:1 より、 AH:HD=6:1
△CDH=△ACD×(1/7)=S/21 、同様にして、△BFG=△AEI=S/21
四角形CHIE=△ACD−2×S/21=S/3−2×S/21=5S/21
同様にして、 四角形BGHD=四角形AIGF=5S/21
よって、△GHI=S−3×5S/21−3×S/21=S/7
以上から、△GHIが、△ABCの面積の1/7の三角形である。
△ADCと直線BEについて、メネラウスの定理より、
(1/2)×(3/2)×DI/AI=1 より、 DI/AI=4/3 すなわち、DI:AI=4:3
ここで、AI=x、IH=y、HD=z とおくと、 x+y:z=6:1 、x:y+z=3:4
x+y=6z 、4x=3y+3z より、zを消去して、 x+y=8x−6y より、 x =y
さらに、x=y=3z であることが分かる。
よって、 AI=IH で、同様にして、 BG=GI 、CH=HG が成り立つ。
すなわち、3本の線分AD、BE、CFは、互いに等しい長さの2本の線分とそうでない線分
に分かれる。
この性質に気が付けば、下図のように面積がすべて等しい7つの三角形に分割されるこ
とが直ちに分かる。
令和元年8月25日付けの(コメント) 視覚的に1/7と分かる別解を考えてみました、も
上記の性質を承知していれば自然な発想であることが分かる。

(追記) 令和2年1月16日付け
平成4年度入試で、次の問題が白百合学園中学から出題されている。