いと思う。読者の皆様からもたくさんのご投稿をお待ちしております。
問題1 AB=3、AC=4、∠A=90°の直角三角形ABCに半円Oが内接している。このと
き、半円の直径DEに対して、線分ECの長さを求めよ。

(解) 半円Oの半径を r 、BO=x とおく。半円Oと辺ABの接点をFとおくと、
△BOFと△BCAが相似なので、 r : 4=x : 5 より、 x=5r/4
△BOFにおいて、三平方の定理より、 (3−r)2+r2=(5r/4)2
これを解いて、 r=12/7 、12 であるが、題意より、 r=12 は不適
よって、 r=12/7 より、求める長さは、
EC=5−(5r/4+r)=5−9r/4=5−27/7=8/7 (終)
S(H)さんから別解をいただきました。(平成31年4月28日付け)
直線 x/3 + y/4=1 上に円 (x-r)^2+(y-r)^2=r^2 の中心(r,r)があるので、
r/3 + r/4=1 より、 r=12/7
そこで、EC=x とおくと、三平方の定理より、
(x+12/7)2=(12/7)2+(4−12/7)2=400/49
よって、 x+12/7=20/7 より、 x=8/7
(コメント) S(H)さんの本解では、
(-(12/7)+x)^2+(-(12/7)+y)^2=144/49 、x/3+y/4=1 から、(24/35,108/35) を採用し、
Sqrt[({0,4}-{24/35,108/35}).({0,4}-{24/35,108/35})]=8/7
または、
(-(12/7)+x)^2+(-(12/7)+y)^2=144/49 、(x-0)^2+(y-4)^2=K^2 が接するようKを定め、
K=8/7 を採用し、K=32/7 は遺棄する
とのことですが、上記ではより易しい新しい道を模索させていただきました。悪しからずご了
承ください。
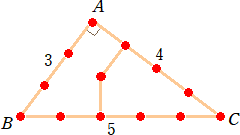
問題2 マッチ棒12本で囲まれた直角三角形ABCがある。AB=3、AC=4、∠A=90°
である。このとき、マッチ棒を2本追加して、この三角形の面積を2等分してください。
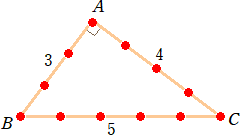
(解) 直角三角形の面積は6なので、次のようにマッチ棒をおけば、それぞれの面積は、
3ずつとなる。
当HPがいつもお世話になっているHN「よおすけ」さんから問題をいただきました。
(令和元年5月2日付け)
問題3 平面上に、3点A(-2,13)、B(-11,1)、C(5,-11)がある。3辺AB、BC、CAの比
AB:BC:CAを最も簡単な整数で表せ。(令和元年5月2日付け)
らすかるさんから解答をいただきました。(令和元年5月2日付け)
(解) A(-2,13)、B(-11,1)、C(5,-11)をBが原点に一致するように平行移動すると、
A’(9,12)、B’(0,0)、C’(16,-12)
C’を原点B’を中心に90°左回転すると、C”(12,16)となり、B’C”=(4/3)B’A’
よって、 ∠ABC=∠A’B’C’=90°であり、また、B’C”=(4/3)B’A’ から、
B’C’=(4/3)B’A’ なので、 AB:BC=A’B’:B’C’=3:4
よって、 AB:BC:CA=3:4:5
(コメント) 素朴に計算してみました。
AB2=81+144=225 、BC2=256+144=400 、CA2=49+576=625 より、
AB2+BC2=CA2 が成り立ち、三平方の定理より、△ABCは、B=90°の直角三角形で、
AB:BC:CA=15:20:25=3:4:5 である。
当HPがいつもお世話になっているHN「カルピス」さんから問題をいただきました。
(令和元年5月5日付け)
問題4 ピタゴラスおじさんの時計は、長針:4cmで短針:3cm。丁度、pm3時にピタッと
時計が止まってしまいました。これはチャンスと、定規で、長針の先から短針の先ま
での長さを測ってみたら、なんと5cmではありませんでした。
あまりにもショックをうけたピタゴラスおじさんは、3時のおやつに用意しておいた 3:4:5
の直角三角柱のチーズケーキを食べられませんでした。
令和になって、「三平方の定理ビックバン」が起きたのかと、悩んでしまいました。
ピタゴラスおじさんを助けてあげてください。なんで5cmにならなかったのでしょうか?
DD++さんからのコメントです。(令和元年5月5日付け)
ピタゴラスおじさんの時計は、「実物」だったから。
実際の時計(すなわち絵に書いたものや液晶で動くタイプではない時計)では、短針の回
転面と長針の回転面は同一ではありません。
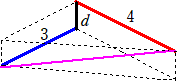
その2つの面の間の距離を d [cm] とすれば、長針の先と短針の先の間の距離は、
√(25+d^2) [cm] になります。
(コメント) 確かに、実際の時計では、長針、短針に段差がありますね!
カルピスさんからのコメントです。(令和元年5月5日付け)
DD++さん、大正解であります(^^)/
長針と短針は同一平面上で回転しないので、5cmより長くなってしまいます。
ps:液晶のアナログ時計の存在には気づきませんでした。あっ、でもピタゴラスおじさんの時
代には、液晶時計は、まだ無かったよーな...。
DD++さんからのコメントです。(令和元年5月5日付け)
ピタゴラスの時代だと、そもそも短針と長針が別々に回転する時計自体がまだないですね。
カルピスさんからのコメントです。(令和元年5月6日付け)
きっと、チーズケーキも無かったですね。
問題5 AB=4の長方形ABCDにおいて、辺BC上にBE=3となる点Eをとり、線分AE上に
点Fを、面積比が △ABE:△AFD:四角形FECD=3:4:5 となるようにとる。
このとき、線分EFの長さを求めよ。
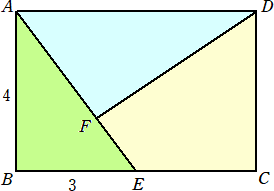
(解) △ABE=6 なので、 △AFD=8 、四角形FECD=10
よって、長方形ABCD=24 となり、 BC=6 であることが分かる。
このとき、△ECD=6 より、 △FED=4 なので、 AF:FE=8:4=2:1
AE=5 なので、EF=5×1/3=5/3 となる。 (終)
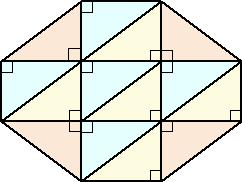
問題6 今、下図のように、3×3 および 4×4 の格子状の正方形がある。
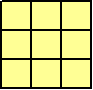

この正方形それぞれを適当に切り分け(線分に沿って切らなくてもよい)、適当に組み合わ
せると、1つの正方形が作られる。どのように分けたらいいのだろうか?

(解) 次のように切り分けて一つの正方形が作られる。(類題→正方形を作る(7))
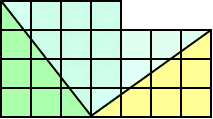
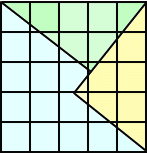
(コメント) 直角三角形3・4・5の問題を意識して解答してみました。
カルピスさんからのコメントです。(令和元年5月8日付け)
与えられた問題文の抜け道がいろいろあるので、解は無限大。
【抜け道その1】 切り分ける枚数が指定されてないので、3x3、4x4を全てバラバラにすれ
ば、5x5に収まる。
【抜け道その2】 「曲線」で切ってはいけないと書いてないので、ジグソーパズルのように切
れば、解は無限に存在する。
#昔、「法律の抜け穴」という本を読んで、凄く面白かったけど、今回は「問題文の隙間を通
り抜ける」...。
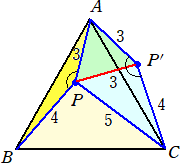
問題7 下図の直角三角形ABCをBを中心として反時計回りに90°回転させる。このとき、
辺ACが通過した図形の面積を求めよ。
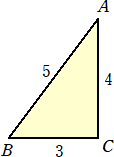
(解) 求める図形は、下図の水色の部分である。

よって、 25π/4+6−(9π/4+6)=4π となる。 (終)
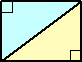
問題8 次の図形の周の長さを求めよ。ただし、直角の記号は図形には含まれない。
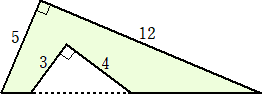
(解) (5+12)+(3+4)+(13−5)=32 (終)
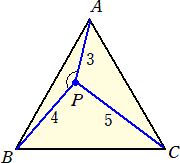
問題9 直角三角形ABCの斜辺AB上に点Pをとったところ、△APCと△PBCの周の長さが
等しくなった。△APCの面積を求めよ。
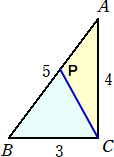
(解) PB=a とおくと、 3+a=4+(5−a) から、 a=3 なので、
AP : PB=2 : 3 より、 △APC=6×(2/5)=12/5 (終)
(追記) 令和5年1月13日付け
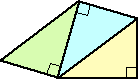
3・4・5の直角三角形がある。内角の大きさは、36.87°、53.13°、90°である。
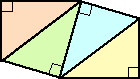
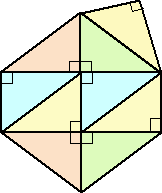
この直角三角形と合同な三角形を何枚か貼り合わせて、凸n角形を作りたい。裏返しや
回転も可として、どこまで作れるだろうか?
下図のように、四角形、五角形、六角形までは何とか作れた。七角形は作れるだろうか?