・　接線の方程式　　　　　　　　　　　　　　　　　　Ｓ．Ｈ氏

　今日、自然対数の底を底とする指数関数　ｙ＝ｅ^ｘ　の接線の方程式を計算していたら、新
鮮な驚きを経験したので報告しておきたい。

　ｘ 軸上の点（ ａ ，０ ）を通り、曲線　ｙ＝ｅ^ｘ　に接する接線の方程式を求めてみる。

接点の座標を、（ ｔ ，ｅ^ｔ ）とおくと、接線の傾きは、ｅ^ｔ であるので、接線の方程式は、

　　　　　　ｙ＝ｅ^ｔ（ ｘ − ｔ ）＋ｅ^ｔ

と書ける。このグラフが、点（ ａ ，０ ）を通るので、

　　　　　　ｅ^ｔ（ ａ − ｔ ）＋ｅ^ｔ＝０

　よって、この式において、　ｅ^ｔ ≠ ０　なので、ｔ ＝ ａ＋１　となる。

　私が感動したのは、ｘ 軸上の点（ ａ ，０ ）を通る接線の接点の ｘ 座標が、ａ＋１　になる
という点である。

　ａ が何であっても、接点の ｘ 座標が、ａ＋１　になるという事実はとても美しい。

今まで指数関数の接線はいい加減に書いていたが、この事実を使えば、正しく綺麗に書け
そうだ。

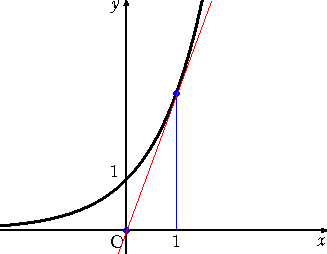
例えば、ｘ＝１ における接線を描くには、 　　　　　ｘ 軸上の点（ ０ ，０ ） を求めて、左図のように直線で結べば、 接線の方程式のグラフが簡単に得られ る。 　（でも、この事は受験数学の世界では 　　常識なのかもしれない。）

上記の事実は、接線影の長さが一定な曲線　ｙ＝Ｃｅ^ｘ　において有用である。（こちらを参照）