４．微分方程式の幾何学的応用 　　　　　　　　　　　　戻る

　ある性質を満たす図形が、微分方程式を介して鮮やかに求めることができる。

例　直線群 Ｙ＝ｍＸ に直交する曲線群を求める

直線群　　Ｙ＝ｍＸ の両辺をＸで微分して、Ｙ’＝ｍ
　Ｙ＝ｍＸ に代入して、ＸＹ’＝Ｙ
　この微分方程式は、直線群 Ｙ＝ｍＸ の満たす
　微分方程式で、直線群 Ｙ＝ｍＸ の持つ幾何
　学的性質を表している。
　　この直線群に直交する曲線群の持つ幾何学
　的性質は、
　　　Ｘ（−１/Ｙ’）＝Ｙ　即ち、　Ｘ＋ＹＹ’＝０
　という微分方程式によって表される。
　両辺の不定積分を求めて、
　　　　　　Ｘ２＋Ｙ２＝ｒ２　　（ｒ は任意定数）
　これは、原点中心の円群である。
　　両者の関係は、左図の通りである。




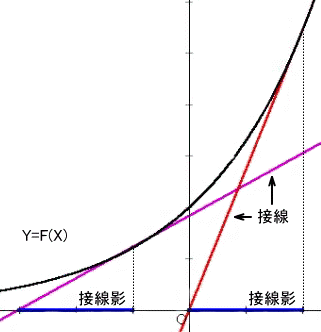
例　接線影の長さが一定な曲線を求める　接線影一定な曲線

　　　接線の方程式は、
　　　　　　　Ｙ＝ｙ’(Ｘ−ｘ)＋ｙ
　　で与えられるので、
　　接線とＸ軸との交点の座標は、
　　　　　　　ｘ−ｙ/ｙ’
　　となる。
　　　このとき、接線影の長さは、
　　　　　　　|ｙ/ｙ’|
　　である。
　　　そこで、例えば、接線影の長さが１と
　　して、次のような微分方程式を考える。
　　　　　　　Ｙ/Ｙ’＝１
　　このとき、
　　　　　　　Ｙ’/Ｙ＝１
　　の両辺の不定積分を求めて、一般解
　　は、
　　　　　　　Ｙ＝ＣｅＸ
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　となる。ただし、Ｃは任意定数。