の値を
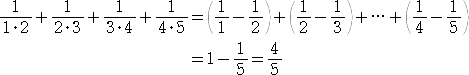
のように求めるとき、何となくスカッとする気分になるのは私だけだろうか。
同じような感覚が味わえる問題がある。
問題 an=tan3n°(n=0、1、2、・・・、20) のとき、
の値を求めよ。
この問題を、次のように解いてみると気分爽快になること間違いなしである。
(解)
より、
よって、求める値は、
問題 次の値を求めよ。
(1+23+43)(1+29+49)(1+227+427)(1+281+481)/(1−2243)
(解) (1+281+481)/(1−2243)=1/(1−281)
(1+227+427)/(1−281)=1/(1−227)
(1+29+49)/(1−227)=1/(1−29)
(1+23+43)/(1−29)=1/(1−23)
より、 与式=−1/7 (終)
問題 次の値を求めよ。
(1−4/9)(1−4/16)(1−4/25)・・・(1−4/n2)
(解)
与式
={(3−2)(3+2)/32}{(4−2)(4+2)/42}{(5−2)(5+2)/52}・・・{(n−2)(n+2)/n2}
=(n−2)!・(1/12)・(2!/n!)・(n+1)(n+2)
=(n+1)(n+2)/{6n(n−1)} (終)
よおすけさんからのコメントです。(平成30年12月14日付け)
数学感動秘話「上手い計算2」も合わせてどうぞ。
次の問題も「スカッとジャパン」相当かな?
問題 次の値を求めよ。
(n+1)(n+2)・・・(n+n−1)(n+n)/{1・3・5・・・・・(2n−1)}
(解) いくつか実験してみると、
3・4/(1・3)=4=22
4・5・6/(1・3・5)=8=23
5・6・7・8/(1・3・5・7)=16=24
以上から、
(n+1)(n+2)・・・(n+n−1)(n+n)/{1・3・5・・・・・(2n−1)}=2n
であることが類推される。この類推が正しいことを数学的帰納法により示す。
n=1のとき、 左辺=2/1=2 、右辺=21=2 で、左辺=右辺
よって、n=1のとき命題は成り立つ。
n=k(k≧1)のとき成り立つと仮定する。すなわち、
(k+1)(k+2)・・・(k+k−1)(k+k)/{1・3・5・・・・・(2k−1)}=2k
n=k+1 のとき、
M=(k+2)・・・(k+1+k−2)(k+1+k−1)(k+1+k)(k+1+k+1)
/{1・3・5・・・・・(2k−1)(2k+1)}
に帰納法の仮定を代入して、
M={2k/(K+1)}・(k+1+k)(k+1+k+1)/(2k+1)=2k+1
よって、n=k+1のときも命題は成り立つ。
したがって、すべての自然数nに対して、
(n+1)(n+2)・・・(n+n−1)(n+n)/{1・3・5・・・・・(2n−1)}=2n
が成り立つ。
(コメント) 数学的帰納法って、あまり「スカッとジャパン」じゃないかな?直接的な証明で、
もっと「スカッとジャパン」な解を募集中です!
PBさんからのコメントです。(平成30年12月19日付け)
お久しぶりです。上記の問題ですが、
(n+1)(n+2)・・・(n+n−1)(n+n)/{1・3・5・・・・・(2n−1)}
=[{1・2・3・・・2n}/{1・2・3・・・n}]・[{2・4・8・・・2n}/{1・2・3・・・(2n−1)・2n}]
={(2n)!/n!}・{(2n・n!)/(2n)!}
=2n
となりますよね.
(コメント) なるほど!こうすれば「スカッとジャパン」ですね。PBさんに感謝します。
tetsuさんからのコメントです。(平成30年12月19日付け)
(n+1)(n+2)(n+3)・・・(n+n-1)(n+n)=(2n)!/n!
また、 1・3・5・・・(2n-1)=1・2・3・・・2n/(2・4・6・・・2n)=(2n)!/(2^n・n!)
したがって、
(n+1)(n+2)(n+3)・・・(n+n-1)(n+n)/{1・3・5・・・(2n-1)}=(2n)!/n!÷{(2n)!/(2^n・n!)}=2^n
らすかるさんからのコメントです。(平成30年12月19日付け)
(n+1)(n+2)・・・(n+n-1)(n+n)/{1・3・5・・・・・(2n-1)}
A[1]、A[2]、A[3]、…、A[n]、B[1]、B[2]、B[3]、…、B[n]の2n個の変数に、1〜2nの異なる
自然数をあてはめることを考える。
A[1]<A[2]<A[3]<…<A[n]を満たすようにあてはめる場合の数は、B[1]〜B[n]にあては
めるn個を決めてから残りのn個を小さい順にA[1]〜A[n]に入れればよいので分子に等しい。
A[1]<A[2]<A[3]<…<A[n] かつ、A[1]<B[1]、A[2]<B[2]、A[3]<B[3]、…、A[n]<B[n]
を満たすようにあてはめる場合の数は、A[1]=1として、B[1]が、2n-1通り、A[2]が残りの数で
最小のもの、B[2]が2n-3通り、A[3]が残りの数で最小のもの、B[3]が2n-5通り、・・・ となる
ので、分母に等しい。
前者は、A[k]>B[k](1≦k≦n)の場合も含み、各kに対して、場合の数が2倍となるので、
分子は分母の2^n倍、従って(与式)=2^n
(コメント) らすかるさんの解法は斬新ですね!勉強になります。
DD++さんからのコメントです。(平成30年12月19日付け)
最初に思いついたのが、PBさん、tetsu さんに書かれてしまったので別の方法で。
n+1 から 2n までの n 個の自然数を全て 2^k*奇数(kは0以上の整数)という形に書いたと
き、この奇数部分には 1 から 2n-1 までの n 個の奇数が1回ずつ出現する。
なぜなら、この表記で同じ奇数を用いるような2つの数は、それらの比が2倍以上でなけれ
ばならないからである。
したがって、約分すれば、この式の値は2の累乗数であり、分子が因数に2をいくつもつか
を考えればよい。
(2n)! が因数に2をいくつ持つか考えると、偶数だけに注目すれば、n! よりちょうど n 個多
いことは明らか。つまり、この式の分子は因数に2をちょうどn個持つ。
よって、この式の値は、2^n である。
らすかるさんからのコメントです。(平成30年12月20日付け)
もう少し簡単な考え方がありました。
1〜2nの数字が書かれたボールが1個ずつあり、2個ずつn組のペアを作ることを考える。
2n個から2個選び、残り2n−2個から2個選び、残り2n−4個から2個選び、・・・ のよう
に考えて場合の数を求めると、n組の順番の分重複するので、
2nC2・2n-2C2・2n-4C2・…・2C2/n!
=(2n)(2n-1)・・・(n+2)(n+1)・n(n-1)・・・2・1/(n!・2n)
=(n+1)(n+2)(n+3)…(2n-1)(2n)/2n (通り)
1とペアにするものは、2n-1通り、残りのうち最小のものとペアにするものは、2n-3通り、そ
の残りのうち最小のものとペアにするものは、2n-5通り、・・・ のように考えて、場合の数を求
めると、
(2n-1)・(2n-3)・(2n-5)・…・3・1 (通り)
従って、 (n+1)(n+2)(n+3)…(2n-1)(2n)/2n=1・3・5・…・(2n-3)・(2n-1) なので、
(n+1)(n+2)(n+3)…(2n-1)(2n)/{1・3・5・…・(2n-3)・(2n-1)}=2n
(コメント) 等式の意味が鮮やかに説明されていて感動しました!らすかるさんに感謝します。
スモークマンさんからのコメントです。(平成30年12月22日付け)
友人Tさんからのものです。(スカッとしてますよね ^^)
n=k のときと n=k+1 のときを比べると、分子は、「k+1」がなくなり、「(k+k+1)(k+k+2)」が追加
される。分母は、「(2k+1)」が追加される。
結局、分数の値は、 ((2k+1)(2k+2)/(k+1))/(2k+1)=2(倍) となることがわかる。
n=1のとき、式は、(1+1)/1=2 なので、一般の自然数 n に対して、 (与式)=2^n
(コメント) なるほど!納得です...。
次は、国際算数数学能力検定(準1級)の問題である。(平成31年2月15日付け)
問題 Σn=1∞ n/(n+1)!の値を求めよ。
(解) 1/1−1/1・2=1/1・2
1/1・2−1/1・2・3=2/1・2・3
・・・・・・・・・・・・・・・・・・・・・・・・・・・
1/1・2・・・・n−1/1・2・・・・(n+1)=n/1・2・・・・(n+1)
よって、辺々加えて、 与式=1−1/(n+1)!
より、 Σn=1∞ n/(n+1)!=1
(コメント) これも美しい消え方ですね!
