マルコフの鎖　　　　　　　　　　　　　　　　　　　　　　　戻る

　　今、次のような問題を考える。

　Ａの袋には１と−1のカードが１枚ずつ、Ｂの袋には０と１のカードが１枚ずつ入っている。Ａ、Ｂ
の袋から、それぞれ１枚のカードを任意に取り出し、互いのカードを交換して袋に戻すという試行
を繰り返す。ｎ回の試行の後、Ａの袋に入っている２枚のカードの数の和がｋになる確率をＰｎ(ｋ)
で表す。ただし、ｎは自然数とする。このとき、Ｐｎ(１)を求めよ。

　ｎ＝２のとき、Ａにおいて和が１となる場合は次の通りである。
{１、−１}⇒{１、−１}⇒{１、０}　　このときの確率は、(１/２)２×(１/２)２＝１/１６
{１、−１}⇒{０、−１}⇒{０、１}　　このときの確率は、(１/２)２×(１/２)＝１/８
{１、−１}⇒{１、１}⇒{１、０}　　　 このときの確率は、(１/２)２×(１/２)＝１/８
{１、−１}⇒{１、０}⇒{１、０}　　　 このときの確率は、(１/２)２×(１/２)２＝１/１６
　　従って、Ｐ２(１)＝３/８ となる。
　ｎ の値が小さい場合は、このようにコツコツ樹形図を書いて求めることができるが、一般の ｎ
について樹形図を書くことは不可能であり実戦的ではない。
　上記問題をじっくり腰を落ち着けて考えると、
袋Ａの状態は、{１、−１}、{１、０}、{０、−１}、{１、１} の４通りしかなく、試行を何回続けても、この
いずれかの状態になっていて、これらの状態を行き来しているにすぎない
ということが、見えてくる。

　試行回数 ｎ＝０，１，２，３，・・・の各場合において定まる観測値Ｘ(ｎ)がある確率変数の実現値
であるとき、{Ｘ(ｎ)} を確率過程と呼ぶ。特に、ｍ＜ｎ とするとき、ｎ における状態の確率が、ｍに
おける状態のみによって定まり、ｍ以前には無関係である、つまり、未来は現在のみに関係し、
過去には関係しないという場合の確率過程のことを、マルコフ過程という。
　マルコフ過程において、確率変数Ｘ(ｎ)のとりうる値が有限個のとき、マルコフの鎖という。
Ｘ(ｎ)のとりうる値を、状態といい、起こりうる状態の集合を、状態空間と呼ぶ。

　上記問題において、袋Ａの数字の和をＸ(ｎ)とすると、状態空間は{−１，０，１，２} となる。これら
の状態間での推移と、それに伴う推移の確率を求めて図示すると、次のような推移図式が得られ
る。
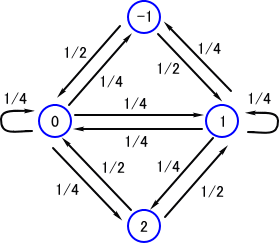推移図式　この推移図式を用いると、Ｐ２(１) の値は次のように
して求められる。
　Ｐ２(１)＝(１/２)Ｐ１(-１)＋(１/４)Ｐ１(０)
　　　　　　　　　　　　　　＋(１/４)Ｐ１(１)＋(１/２)Ｐ１(２)
　状態０から出発するので、
　　Ｐ１(-１)＝Ｐ１(０)＝Ｐ１(１)＝Ｐ１(２)＝１/４
　従って、Ｐ２(１)＝(３/２)×(１/４）＝３/８　となる。
　　
　　一般に、
　Ｐｎ(１)＝(１/２)Ｐｎ−１(-１)＋(１/４)Ｐｎ−１(０)
　　　　　　　　　　　＋(１/４)Ｐｎ−１(１)＋(１/２)Ｐｎ−１(２)
　同様にして、
　Ｐｎ(-１)＝(１/４)Ｐｎ−１(０)＋(１/４)Ｐｎ−１(１)
　Ｐｎ(０)＝(１/２)Ｐｎ−１(-１)＋(１/４)Ｐｎ−１(０)
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　＋(１/４)Ｐｎ−１(１)＋(１/２)Ｐｎ−１(２)
　　　　　　　　　　　　　　　　　　　　　　　　　　　Ｐｎ(２)＝(１/４)Ｐｎ−１(０)＋(１/４)Ｐｎ−１(１)
　これらを整理すると、
　　　　　　　Ｐｎ(１)＝Ｐｎ−１(-１)＋(１/２)Ｐｎ−１(１)、　Ｐｎ(-１)＝(１/２)Ｐｎ−１(１)

従って、　Ｐｎ(１)＋Ｐｎ(-１)＝Ｐｎ−１(１)＋Ｐｎ−１(-１)＝Ｐ１(１)＋Ｐ１(-１)＝１/２　・・・・（＊）
また、
　　Ｐｎ(１)−２Ｐｎ(-１)＝Ｐｎ−１(-１)−(１/２)Ｐｎ−１(１)＝(−１/２)(Ｐｎ−１(１)−２Ｐｎ−１(-１))　より、
　　　　　　Ｐｎ(１)−２Ｐｎ(-１)＝−(−１/２)ｎ＋１・・・・（＊＊）

（＊）（＊＊）から、連立方程式を解いて、
　　　　　　　　　　　　　　　　　Ｐｎ(１)＝(１/３)(１−(−１/２)ｎ＋１)

（参考文献：渡部隆一　著　確率（共立出版）
　　　　　　　 岡安　實　著　確率・統計（旺文社））