皆敷の数理　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　皆敷（かいしき）とは、正月の供え餅や和菓子と器との間に敷くものを言う。以前は、ナン
テン、ヒバなどの常緑樹の葉が用いられたものだが、最近は縁取りが紅の正方形の紙を
用いることが多い。スーパーなどで売られているお供え用の餅には正方形のままであるが、
正式には半分に折って敷くものらしい。

　　　　　

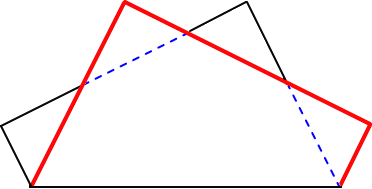
　このとき、下図の４つの三角形の面積が全て同じになるように折るのが正式である。

　　　　　


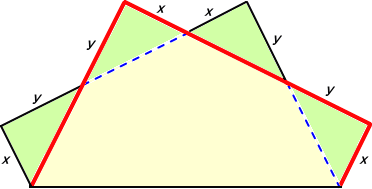
　ｘ と ｙ の間にどのような関係があるか計算してみよう。　正方形の１辺の長さを ａ とする。

　三平方の定理を用いて、　　　ｘ²＋ｙ²＝（ａ−ｘ−ｙ）²

よって、これを解いて、　ｙ＝ａ（ａ−２ｘ）/｛２（ａ−ｘ）｝　を得る。

　このことから、条件を満たす折り方は無数にあることが分かるが、現実的には次のような
折り方をすれば十分であろう。

　ｘ＝ａ/４　のとき、　ｙ＝ａ/３　となるので、正方形の縦、横を４等分、３等分して、その等分
点を通るように正方形の辺を重ねて折る。

　何でもないことだが、一つのエチケット、常識として覚えておくといいと思う。