魔星陣　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　

左図において、各線上の４つの数の和が等しいように 　　相異なる１０個の数を入れていくパズルがある。 　　　このようなパズルは、５星陣の問題といわれる。 　　１０個の数として、次のような場合が考えられる。 　　　１、２、３、４、５、６、８、９、１０、１２ 　　　１、２、３、４、５、６、７、９、１０、１３ 　　これらは、線分の最小の和を与える場合である。

　たとえば、次のような配列が知られている。

　　　　　　　　　　　　　　　

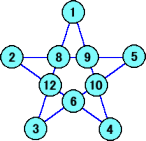
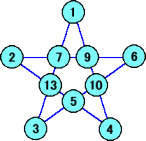
　魔星陣というと、その美しさが光るが、５星陣には非常に残念で致命的な欠点がある。

すなわち、

　　　５星陣を、１から始まる連続数で作ることは不可能である

ということである。

（証明）　５星陣が、１から始まる連続数で作れたものと仮定する。
　　　　このとき、各線上の４つの数の和は、２２である。

　　　　数 １ がのっている２本の線上のどちらかに、数 １０ がのっている。

　　　　　実際に、数 １ がのっている２本の線上の数 １ 以外の６つの数の和は４２である。
　　　　もし、どちらにも数 １０ がのっていなければ、
　　　　６つの数の和は、高々９＋８＋７＋６＋５＋４＝３９ であるので、これは矛盾である。

　　　　そこで、数 １ と数 １０ を通る線分を Ｌ、数 １ を通る他の線分をＭ、Ｌ とは異なる数
　　　　１０ を通る線分をＮとおく。

　　　　　このとき、可能な場合は次の表で与えられる。

　　　　もともと存在しない場合は除いて、他の場合において、ＭとＮに共通する数がない。
　　　これは、どんな２つの線分も共通する数が１個はなければならないことに矛盾する。
　　　　したがって、５星陣を、１から始まる連続数で作ることは不可能である。（証明終）

　このことから、冒頭に掲げたような飛び飛びの数でしか、５星陣は作れないのである。

（参考文献：大森清美　著　魔方陣　（冨山房））

（追記）　平成２０年１０月１１日付け

　当ＨＰの掲示板「出会いの泉」に、１０月１０日付けでＨＮ「ＧＡＩ」さんが、６角魔方陣の話
題を提供された。ＧＡＩさんに感謝いたします。

　下図のように、１９個の円形の空所が互いに線で結ばれており、直線上に並ぶ円に書か
れた数の総和が常に等しくなるように、１から１９までの自然数を配置するというパズルが
ある。

　　　

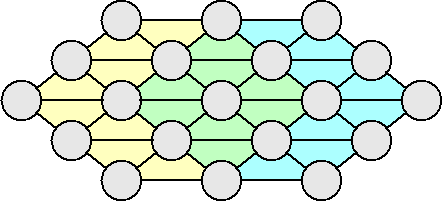
　１から１９までの自然数の総和は、１９（１＋１９）/２＝１９０ で、１９０÷５＝３８ から、直線
上に並ぶ円に書かれた数の総和は常に３８となることが分かる。

　１から１９までの自然数を、総和が３８となるように３〜５個の組合せを３種類作ればいい
のだろうが、論理的に円に数字を埋めていくのは結構難しそうな．．．予感！

　ＧＡＩさんによれば、次のような解があるそうである。

　　　

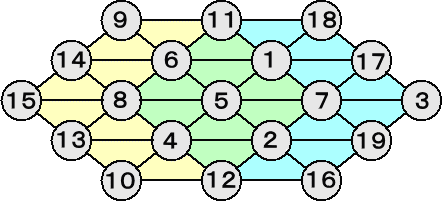
　解が、「これだけ！」ということは確認されていない。

（追記）　　当ＨＰがいつもお世話になっているらすかるさんが検証された。回転と裏返しを
　　　　　同一視して１通りしか解はないとのことである。

　私自身もっとあるかな？と思っていましたが、１通りと聞いて驚きです。ＧＡＩさんのお言葉
を借りれば、「見事なバランス」の一語に尽きますね！ご検証いただいた、らすかるさんに
感謝します。