計算する図　　　　　　　　　　　　　　　　　　　　　　　　

　レンズは、両側の面が球面になっている透明体である。レンズの軸上にある光点Ａから出た
光が、どこに像を生じるかは、光学での一つの興味あるテーマとなっている。

　　　　　　　
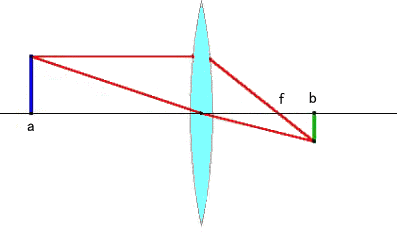
　レンズの中心Ｏから光源Ａまでの距離を ａ、レンズの中心Ｏから像Ｂまでの距離を ｂ、レン
ズの中心Ｏから焦点Ｆまでの距離を ｆ とすると、次のようなレンズの公式が成り立つ。

　　　　　　　　　　　　　

　ただし、ａ、ｂ、ｆ は正負をつけて考えるものとする。

　　光源については、レンズの前方のとき・・・・・　ａ＞０
　　　　　　　　　　　　レンズの後方のとき・・・・・　ａ＜０

　　像については、レンズの後方（実像）のとき・・・・・　ｂ＞０
　　　　　　　　　 　レンズの前方（虚像）のとき・・・・・　ｂ＜０

　　焦点距離（像空間焦点距離）については、凸レンズのとき・・・・・　ｆ＞０
　　　　　　　　　　　　　　　　　　　　　　　　　 　凹レンズのとき・・・・・　ｆ＜０

　練習問題を一つやってみよう。

練習問題　　焦点距離５０ｃｍの凸レンズの前方２５ｃｍにある光点の像の位置を求めよ。
　　　　　　　また、実像か虚像かを明らかにせよ。

（解）　レンズの公式より、　１/２５＋１/ｂ＝１/５０　より、　ｂ＝−５０

　　　よって、レンズの前方５０ｃｍのところに虚像ができる。　　（終）

　
　このように、光学の世界では、レンズの公式を解くことが多い。これに対して、次のような
計算図表が知られている。

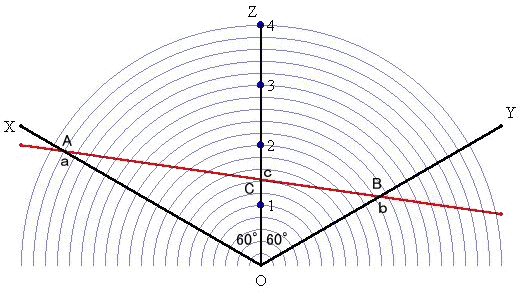
　上図で、Ｘ軸とＺ軸、Ｙ軸とＺ軸はそれぞれ ６０°の角をなす。また、各軸の目盛は同じも
のとする。

（計算図表の使い方）
例えば、ａ＝３．８、ｂ＝２．３　のとき、		を満たすｃ の値を求めるには、上図
の赤線に定規をあわせ、ｃ の値を読み取ればよい。　ｃ＝１．４２ 位と読み取れるでしょう。 (実際に、計算で求めると、ｃ＝１．４３２　位）

数学的背景　　　　△OAB＝△OAC＋△OBC より、

　　　　　　　　　(１/２)ａｂsin１２０°＝(１/２)ａｃsin６０°＋(１/２)ｂｃsin６０°である。

　　　　　　　　よって、ａｂ＝ａｃ＋ｂｃ　となり、両辺を ａｂｃ で割って、

　　　　　　　　　　　　　　　　　　　


　私が高校のときに学んだ教科書に、次のような問題があった。

　点Ｏから出る３つの半直線ＯＸ、ＯＹ、ＯＺがあって、∠ＸＯＺ＝∠ＺＯＹ＝６０°とする。１つ
の直線が、ＯＸ、ＯＹ、ＯＺと交わる点をそれぞれＡ、Ｂ、Ｃとし、ＯＡ＝ａ、OB＝ｂ、OＣ＝ｃ とお
くとき、
　　　　　　　　　　　　　
が成り立つことを示せ。

　在学中は、単なる面積の公式の応用問題という認識しかなく、その重要性にあまり気づか
なかった。今はじめてその意味を知り、その性質の素晴らしさに驚いている。

（参考文献：コロソフ著　木村君男　訳　数学課外よみもの（東京図書））


（追記）　レンズの公式を用いる問題に最近遭遇した。（平成２７年２月１６日付け）

　焦点距離 ｆ の凸レンズの左方１５ｃｍのところに長さａのローソクをおいたら、凸レンズの
右方に長さ２ａの像ができた。このとき、ｆ の値を求めよ。

（解）　レンズの公式より、　１/１５＋１/３ｆ＝１/ｆ　が成り立つので、両辺を１５ｆ 倍して、

　　　ｆ＋５＝１５　　よって、求める焦点距離は、ｆ＝１０（ｃｍ）　　（終）


（追記）　当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんから、上記の「数学的背景」
　　　　　で用いられた手法の類題をいただきました。（令和３年１０月１６日付け）

　△ABCの辺BC上に点Dがある。∠BAD＝α、∠CAD＝β、AB＝y、AC＝x、AD＝zとおく。

　　　

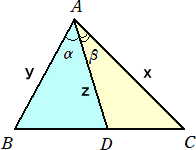
　このとき、　sinA/z＝sinα/x＋sinβ/y　が成り立つことを証明せよ。

（解）　△ＡＢＣ＝△ＡＢＤ＋△ＡＤＣ　より、

　　　（１/２）ｘｙ・ｓｉｎＡ＝（１/２）ｙｚ・ｓｉｎα＋（１/２）ｚｘ・ｓｉｎβ

　　両辺を（１/２）ｘｙｚ で割って、　sinA/z＝sinα/x＋sinβ/y　が成り立つ。　　（終）