垂線の足の距離 　　　　　　　　　　　　　　　　　　　　　　　　　　　

　△ＡＢＣの辺ＢＣ上の点Ｐより、辺ＡＢ、ＡＣに下ろした垂線の足を、それぞれＭ、Ｎとおく。

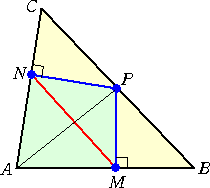このとき、 　　　　　ＭＮ＝ＡＰ・ｓｉｎＡ 　が成り立つ。 （コメント）　何となくスッキリした定理で、知っていると得す 　　　　　　るような．．．予感。

　証明は、余弦定理を用いて容易に示すことができる。

（証明）　ＡＭ＝ＡＰ・ｃｏｓ α　、　ＡＮ＝ＡＰ・ｃｏｓ β　であるので、余弦定理により、

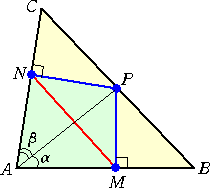ＭＮ2＝ＡＭ2＋ＡＮ2−２ＡＭ・ＡＮ・ｃｏｓ（ α ＋ β ） ＝ＡＰ2・ｃｏｓ2 α＋ＡＰ2・ｃｏｓ2 β 　−２ＡＰ2・ｃｏｓ α・ｃｏｓ β・ｃｏｓ（ α ＋ β ） 　ここで、 　ｃｏｓ（ α ＋ β ）＝ｃｏｓ α・ｃｏｓ β−ｓｉｎ α・ｓｉｎ β 　なので、

ＭＮ²

＝ＡＰ²・（ｃｏｓ² α＋ｃｏｓ² β−２ｃｏｓ² α・ｃｏｓ² β＋２ｓｉｎ α・ｓｉｎ β・ｃｏｓ α・ｃｏｓ β）

＝ＡＰ²・（ｃｏｓ² α・（１−ｃｏｓ² β）＋ｃｏｓ² β・（１−ｃｏｓ² α）
　＋２ｓｉｎ α・ｓｉｎ β・ｃｏｓ α・ｃｏｓ β）

＝ＡＰ²・（ｃｏｓ² α・ｓｉｎ² β＋ｓｉｎ² α・ｃｏｓ² β＋２ｓｉｎ α・ｓｉｎ β・ｃｏｓ α・ｃｏｓ β）

＝ＡＰ²・（ｓｉｎ α・ｃｏｓ β＋ｃｏｓ α・ｓｉｎ β）²

＝ＡＰ²・ｓｉｎ²（ α ＋ β ）

　ｓｉｎ（ α ＋ β ）＞０　なので、　　ＭＮ＝ＡＰ・ｓｉｎ（ α ＋ β ）＝ＡＰ・ｓｉｎＡ

が成り立つ。　（証終）

　証明を書き上げて、ボーッと図を眺めていると、上記の証明よりも易しい証明があること
に気づいた。


（別証）　題意より、四角形ＡＭＰＮは円に内接する四角形で、ＡＰが直径である。

　よって、△ＡＭＮに正弦定理を適用して、　ＭＮ＝ＡＰ・ｓｉｎＡ　が成り立つ。　（別証終）


（コメント）　こんな別証があるなんて、「ガ〜ン！」ですね！もっとも、こちらの方を先に思い
　　　　　　浮かぶ方の方が多いかも．．．。


（追記）　令和５年１１月４日付け

　Ｃ＝９０°の直角三角形ＡＢＣにおいて、頂点Ｃから斜辺ＢＣに垂線を下ろし、その足をＨ
とおき、ＣＨ＝ｈ とする。また、ＢＣ＝ａ、ＣＡ＝ｂ とおく。

　　

このとき、

　

が成り立つ。

（証明）　三平方の定理より、　ＡＢ²＝ａ²＋ｂ²　である。

　また、△ＡＢＣの面積を求めて、　ａｂ/２＝ＡＢ・ｈ/２　から、　ａ²ｂ²＝ＡＢ²・ｈ²

よって、　ａ²ｂ²＝（ａ²＋ｂ²）・ｈ²　から、　１/ｈ²＝（ａ²＋ｂ²）/ａ²ｂ²＝１/ａ²＋１/ｂ²

したがって、

　

が成り立つ。　　（証終）


例　ａ＝３、ｂ＝４ の直角三角形ＡＢＣにおいて、頂点Ｃから斜辺ＡＢに下した垂線ＡＨの長さ
　ｈ について、

　１/ｈ²＝１/３²＋１/４²＝２５/１４４

より、　ｈ＝１２/５　である。


　光源から距離 ｒ だけ離れた場所での光の強さは、ｒ²の逆数に比例するという法則がある。

例えば、点（０，１）に光源Ｈを置いたとき、原点で感じる光の強さは、光源Ｈを２点（−１，１）

（１，１）のそれぞれに置いたときに感じる光の強さは、相等しい。

　　

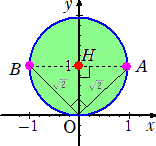
　Ａ、Ｂから感じる光の強さは、（）²の逆数に比例し、公式

　

から、原点Ｏで感じる光源Ｈの光の強さは、２点Ａ、Ｂから感じる光の強さに等しい。


（コメント）　一つの光源が２箇所に転移することが、数学的に説明されるんですね！



　　以下、工事中！