
大圏航路は、英訳すると、great−circle course と書かれるように、地球を球面と見
なし、球の中心を通る平面と球面の交線(大円)上を辿る航路である。他の制約条件(燃料
補給の空港の確保、偏西風を利用する航路など)を除けば、純粋に最短経路であると言え
る。
この大圏航路に関する話題が、平成20年度入試 京都大学 理系・乙 にて問われた。
地球上の北緯60°東経135°の地点をA、北緯60°東経75°の地点をBとする。
AからBに向かう2種類の飛行経路R1、R2を考える。R1は西に向かって同一緯度で
飛ぶ航路とする。R2は地球の大円に沿った経路のうち飛行経路の短い方とする。R1
に比べて、R2は飛行距離が3%以上短くなることを示せ。ただし、地球は完全な球体
とし、飛行機は高度0を飛ぶものとする。
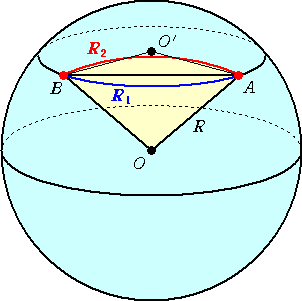
(解) 地球の半径を R とする。地球と、赤道面に平行な平面との切り口で、2点 A、B を通
る円の半径は、 R・cos60°=R/2 である。ここで、 135°−75°=60°は、π/3
ラジアンであるので、 R1=(R/2)×π/3=πR/6 となる。
また、 AB=2×(R/2)×sin30°=R/2 である。
地球の中心を O とし、 ∠AOB=θ とおくと、余弦定理により、
(R/2)2=R2+R2−2R・R・cosθ
よって、 cosθ=7/8 となるθを用いて、 R2=R・θ と書ける。
題意を示すためには、 R2=R・θ≦(πR/6)×0.97 であることを言えばよい。
ここで、 (π/6)×0.97=30°×0.97=29.1°である。
ところで、 cosθ=7/8=0.875 で、三角比の表より、 cos29°=0.8746 な
ので、 θ<29°であることが分かる。
以上から、 R2=R・θ≦(πR/6)×0.97 が成り立つので、R1 に比べて、R2 は
飛行距離が3%以上短くなる。 (終)
(コメント) このような「評価」の問題は、受験生泣かせですよね!上記の解答も、後半部分
が何となくしっくりこないような...雰囲気。しっくりくるためには、ガチガチに評価
式を操るしかないです。次のように計算するといいのかな?
cosθ=7/8=0.875 で、三角比の表より、
cos29.0°=0.8746 、 cos28.5°=0.8788
なので、 28.5°<θ<29.0° となる。弧度法で表すと、
(28.5)×(π/180)<θ<29.0×(π/180)
したがって、
R2/R1=(R・θ)/(πR/6)=6θ/π<(6/π)・29×(π/180)=29/30
ここで、 29/30=0.9666 ・・・・ なので、確かに、R1 に比べて、R2 は飛行距離が
3%以上短くなることが分かる。
ところで、京都大学の問題設定「北緯60°」は、あまりに北すぎて、日本という感じがない
ところが惜しいところである。因みに北緯60°の有名都市といえば、ノルウェイのオスロに
なるのだが...。
東京はだいたい北緯35°東経140°に位置するので、京都大学の問題を次のように変形
してみよう。
地球上の北緯35°東経140°の地点をA、北緯35°東経50°の地点をBとする。
AからBに向かう2種類の飛行経路R1、R2を考える。R1は西に向かって同一緯度で
飛ぶ航路とする。R2は地球の大円に沿った経路のうち飛行経路の短い方とする。
このとき、R1に比べて、R2の飛行距離は何%以上短くなるかを求めよ。
ただし、地球は完全な球体とし、飛行機は高度0を飛ぶものとする。
因みに、北緯35°東経50°に位置する有名都市はイランの首都テヘランである。
(テヘランというともっと南にあるかと思いきや、意外にも東京と同緯度なんですね!)
解法は、京都大学の場合と同様である。
(解) 地球の半径を R とする。地球と、赤道面に平行な平面との切り口で、2点 A、B を通
る円の半径は、 R・cos35°である。ここで、 140°−50°=90°は、π/2 ラジアンで
あるので、 R1=(R・cos35°)×π/2=πR・cos35°/2 となる。
また、 AB=2×(R・cos35°)×sin45°=
地球の中心を O とし、 ∠AOB=θ とおくと、余弦定理により、
(
よって、 cosθ=1−cos235°となるθを用いて、 R2=R・θ と書ける。
ここで、 cosθ=1−cos235°=sin235°=(1−cos70°)/2 で、
cos70°=0.3420 より、 cosθ=0.3290 となる。
三角比の表より、
cos71.0°=0.3256 、 cos70.5°=0.3338
なので、 70.5°<θ<71.0° となる。弧度法で表すと、
(70.5)×(π/180)<θ<71.0×(π/180)
したがって、
R2/R1=(R・θ)/(πR・cos35°/2)=(2θ/π)・(1/cos35°)
三角比の表より、 cos35°=0.8192 なので、
R2/R1<(2/π)・71×(π/180)×(1/cos35°)=71/(90×0.8192)
よって、 R2/R1<0.962999 ・・・
このことから、 R1 に比べて、R2 は飛行距離が、3.7%以上短くなることが分かる。
(コメント) 京都大学の場面設定に比べて赤道に近いので、それほどの違いはないだろう
と予想したのですが、結構違うものですね!大圏航路の問題は、三角比の知識
をいろいろ用いるので、応用問題として最適ですね。入試問題として出題された
京都大学に敬意を表します。