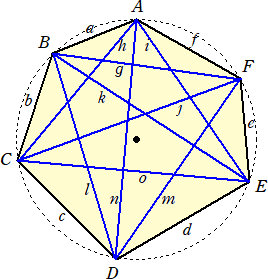
円周上に、反時計回りに４点Ａ、Ｂ、Ｃ、Ｄが配置されている。
（１） △ＡＣＤは１辺の長さが３の正三角形で、線分ＢＤは円の直径である。
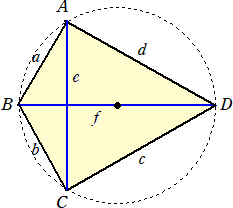
今、Ａxを、Ａ以外の３点からなる三角形の３辺の長さの積、すなわち、Ａx＝ｂｃｆ とする。
同様に、
Ｂxを、Ｂ以外の３点からなる三角形の３辺の長さの積、すなわち、Ｂx＝ｃｄｅ とする。
Ｃxを、Ｃ以外の３点からなる三角形の３辺の長さの積、すなわち、Ｃx＝ａｄｆ とする。
Ｄxを、Ｄ以外の３点からなる三角形の３辺の長さの積、すなわち、Ｄx＝ａｂｅ とする。
このとき、 Ａx−Ｂx＋Ｃx−Ｄx の値を求めよ。
（解） 題意より、 ｃ＝ｄ＝ｅ＝３ で、ａ＝ｂ＝
、ｆ＝２ なので、Ａx＝ｂｃｆ＝１８ 、Ｂx＝ｃｄｅ＝２７ 、Ｃx＝ａｄｆ＝１８ 、Ｄx＝ａｂｅ＝９
よって、 Ａx−Ｂx＋Ｃx−Ｄx＝１８−２７＋１８−９＝０ （終）
（２） △ＡＣＤは、ｃ＝６、ｄ＝８、ｅ＝１０ の直角三角形で、△ＡＢＣは∠Ｂ＝９０°の直角二
等辺三角形である。
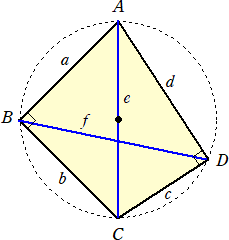
このとき、 Ａx−Ｂx＋Ｃx−Ｄx の値を求めよ。
（解） 題意より、 ｃ＝６、ｄ＝８、ｅ＝１０ で、ａ＝ｂ＝５
である。また、余弦定理より、
ｆ2＝（５
）2＋６４−８０ｃｏｓ∠ＢＡＤ＝（５）2＋３６−６０ｃｏｓ∠ＢＣＤここで、 ｃｏｓ∠ＢＣＤ＝ｃｏｓ（π−∠ＢＡＤ）＝−ｃｏｓ∠ＢＡＤ なので、
（５
）2＋６４−８０ｃｏｓ∠ＢＡＤ＝（５）2＋３６＋６０ｃｏｓ∠ＢＡＤすなわち、１１４−８０
ｃｏｓ∠ＢＡＤ＝８６＋６０ｃｏｓ∠ＢＡＤ より、ｃｏｓ∠ＢＡＤ＝１/（５
）よって、 ｆ2＝１１４−８０
ｃｏｓ∠ＢＡＤ＝９８ より、 ｆ＝７このとき、
Ａx＝ｂｃｆ＝４２０ 、Ｂx＝ｃｄｅ＝４８０ 、Ｃx＝ａｄｆ＝５６０ 、Ｄx＝ａｂｅ＝５００
よって、 Ａx−Ｂx＋Ｃx−Ｄx＝４２０−４８０＋５６０−５００＝０ （終）
（３） （１）（２）の結果から、次のことが推察される。すなわち、
円周上に、反時計回りに４点Ａ、Ｂ、Ｃ、Ｄが配置されている場合
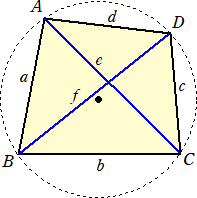
について、Ａx−Ｂx＋Ｃx−Ｄx＝０ が成り立つ。
この推察が正しいことを証明せよ。
（証明） （２）の ｆ の計算と同様に、余弦定理から、
ｅ2＝ａ2＋ｂ2−２ａｂ・ｃｏｓ∠ＡＢＣ＝ｃ2＋ｄ2−２ｃｄ・ｃｏｓ∠ＡＤＣ
ｃｏｓ∠ＡＤＣ＝−ｃｏｓ∠ＡＢＣ なので、
ａ2＋ｂ2−２ａｂ・ｃｏｓ∠ＡＢＣ＝ｃ2＋ｄ2＋２ｃｄ・ｃｏｓ∠ＡＢＣ より、
ｃｏｓ∠ＡＢＣ＝（ａ2＋ｂ2−ｃ2−ｄ2）/（２ａｂ＋２ｃｄ）
よって、
ｅ2＝ｃ2＋ｄ2＋ｃｄ（ａ2＋ｂ2−ｃ2−ｄ2）/（ａｂ＋ｃｄ）＝（ａｃ＋ｂｄ）（ａｄ＋ｂｃ）/（ａｂ＋ｃｄ）
から、 ｅ＝√｛（ａｃ＋ｂｄ）（ａｄ＋ｂｃ）/（ａｂ＋ｃｄ）｝
同様に、
ｆ2＝ａ2＋ｄ2−２ａｄ・ｃｏｓ∠ＢＡＤ＝ｂ2＋ｃ2−２ｂｃ・ｃｏｓ∠ＢＣＤ
ｃｏｓ∠ＢＣＤ＝−ｃｏｓ∠ＢＡＤ なので、
ａ2＋ｄ2−２ａｄ・ｃｏｓ∠ＢＡＤ＝ｂ2＋ｃ2＋２ｂｃ・ｃｏｓ∠ＢＡＤ より、
ｃｏｓ∠ＢＡＤ＝（ａ2＋ｄ2−ｂ2−ｃ2）/（２ａｄ＋２ｂｃ）
よって、
ｆ2＝ｂ2＋ｃ2＋ｂｃ（ａ2＋ｄ2−ｂ2−ｃ2）/（ａｄ＋ｂｃ）＝（ａｂ＋ｃｄ）（ａｃ＋ｂｄ）/（ａｄ＋ｂｃ）
から、 ｆ＝√｛（ａｂ＋ｃｄ）（ａｃ＋ｂｄ）/（ａｄ＋ｂｃ）｝
このとき、
Ａx−Ｂx＋Ｃx−Ｄx
＝ｂｃｆ−ｃｄｅ＋ａｄｆ−ａｂｅ＝（ａｄ＋ｂｃ）ｆ−（ａｂ＋ｃｄ）ｅ
＝√｛（ａｂ＋ｃｄ）（ａｃ＋ｂｄ）（ａｄ＋ｂｃ）｝−√｛（ａｃ＋ｂｄ）（ａｄ＋ｂｃ）（ａｂ＋ｃｄ）｝
＝０
であることが示された。 （証終）
（コメント） 美しい結果ですね！感動しました。
四角形では、全部で 4Ｃ2＝６（本） の線分があり、１つの頂点を除いた他の３点を結ぶ線
分は、3Ｃ2＝３（本） で、計算も比較的簡単であった。円に内接する四角形の性質が使えた
のが大きかった。
それでは、問題をもう少し拡張して、六角形の場合にも同様のことが言えるのだろうか？
六角形では、全部で 6Ｃ2＝１５（本） の線分があり、１つの頂点を除いた他の５点を結ぶ線
分は、5Ｃ2＝１０（本） で、計算も爆発的に増大する。
一般の六角形では、全く途方に暮れてしまうので、特別な六角形に対して計算してみよう。
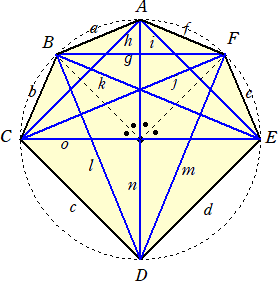
上図では、半径１の円に内接する六角形で、ＡＤとＣＥは互いに直交する直径とする。Ｂ、Ｆ
はそれぞれ弧ＡＣ、ＡＥの中点である。１５本の線分の長さ
ａ 、ｂ 、ｃ 、ｄ 、ｅ 、ｆ 、ｇ 、ｈ 、ｉ 、ｊ 、ｋ 、ｌ 、ｍ 、ｎ 、ｏ
をそれぞれ求めていこう。
ａ＝ｂ＝ｅ＝ｆ ： 余弦定理より、ａ2＝ｂ2＝ｅ2＝ｆ2＝１＋１−２（
/２）＝２− なので、ａ＝ｂ＝ｅ＝ｆ＝√（２−
）ｃ＝ｄ＝ｇ＝ｈ＝ｉ ： 明らかに、ｃ＝ｄ＝ｇ＝ｈ＝ｉ＝
ｊ＝ｋ＝ｌ＝ｍ ： 三平方の定理より、ｊ2＝ｋ2＝４−（２−
）＝２＋ なので、ｊ＝ｋ＝ｌ＝ｍ＝√（２＋
）ｎ＝ｏ ： 明らかに、ｎ＝ｏ＝２
ここで、頂点Ａを除いた他の５点間の線分の長さの積を、Ａx と表す。他の Ｂx、Ｃx、Ｄx、
Ｅx、Ｆx も同様である。
Ａx、Ｂx、Ｃx、Ｄx、Ｅx、Ｆx の計算で、使わない辺の長さを、下表の通り「×」で示す。
