平面上に相異なる２点Ａ、Ｂを与えるとき、それらから等距離にある点の集合として、直
線がただ一つ存在し、その直線は、線分ＡＢの垂直２等分線と言われる。
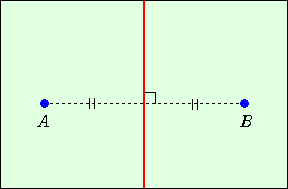
空間においても同様の問題を考えることが出来る。すなわち、
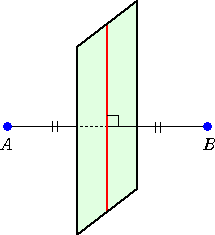
空間において相異なる２点Ａ、Ｂを与えるとき、それらから等距離にある点の集合として、
平面はただ一つ存在する。
この平面は、線分ＡＢの中点を通り、線分ＡＢに垂直な平面である。
上記では、２点Ａ、Ｂから等距離にある点の集合としての図形を考えたが、ある図形があ
って、２点Ａ、Ｂから等距離にあるという条件を考えると、事情は一変し、上記の直線や平
面に限らずにもっと無数の直線や平面が存在することになる。
（この件で、当ＨＰがいつもお世話になっているらすかるさんからアドバイスを頂きました。）
例えば、平面においては線分ＡＢに平行な直線、空間においては線分ＡＢに平行な平面
がそうである。
空間において、同一直線上にない３点を考えると、その３点を通る平面はただ１つ存在し、
したがって、それらの３点から等距離にある平面は無数に存在する。この場合、平面の個
数を問うてみても、問題にならない。
しかし、この視点で、問題を考えることは、あながち無駄ではないだろう。
そこで、次のような問題を考えることにする。
空間において、同一平面上にない４点Ａ、Ｂ、Ｃ、Ｄを与えるとき、これらの点から
等距離にある平面は幾つ存在するか？
一見すると難しそうに感じるかもしれないが、
「同一平面上にない４点Ａ、Ｂ、Ｃ、Ｄを与える」ということを、
「空間において、四面体ＡＢＣＤが与えられている」と考えれば、解法の糸口が見えて
くることだろう。
２つの場合が考えられる。
（１） 求める平面の片側に３点、反対側に１点の配置になっている場合
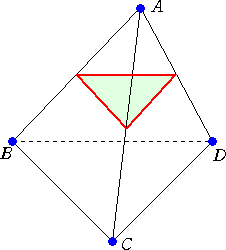Ａ−ＢＣＤ のとき、線分ＡＢ、線分ＡＣ、線分ＡＤの中点を通る平面
が求める平面で、ただ１つ存在する。
同様にして、 Ｂ−ＣＤＡ 、Ｃ−ＤＡＢ 、Ｄ−ＡＢＣ
の場合も各１面ずつ存在する。
よって、この場合の平面の個数は、４個である。
（２） 求める平面の片側に２点、反対側に２点の配置になっている場合
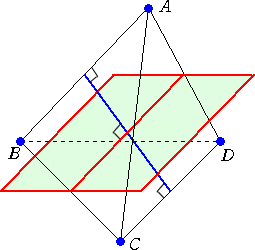ＡＢ−ＣＤ のとき、線分ＡＤ、線分ＢＣの中点を結ぶ直線を含み、
線分ＡＢ、ＣＤに平行な平面が求める平面で、
ただ１つ存在する。
同様にして、 ＡＣ−ＢＤ 、ＡＤ−ＢＣ
の場合も各１面ずつ存在する。
よって、この場合の平面の個数は、３個である。
以上から、求める平面の個数は、 ４＋３＝７（個） である。
さらに、次のような問題を考える。
空間において、同一平面上にもなく同一球面上にもない５点Ａ、Ｂ、Ｃ、Ｄ、Ｅを与え
るとき、これらの点から等距離にある平面または球面は幾つ存在するか？
答えは、１５個だが、十分難しそうに感じますね！
考え方は上記の問題と同様である。以下の２つの場合が考えられる。
（１） 求める平面（または球面）の片側に４点、反対側に１点の配置になっている場合
Ａ−ＢＣＤＥ のとき、
４点Ｂ、Ｃ、Ｄ、Ｅ が同一直線上、同一円周上に存在することはないので、４点Ｂ、Ｃ、
Ｄ、Ｅ を通る平面（または球面）がただ一つ存在する。
このとき、明らかに、この平面（または球面）と点Ａから等距離にある平面（または球
面）がただ一つ存在する。
同様にして、 Ｂ−ＣＤＥＡ 、Ｃ−ＤＥＡＢ 、Ｄ−ＥＡＢＣ 、Ｅ−ＡＢＣＤ
の場合も各１面ずつ存在する。
よって、この場合の平面（または球面）の個数は、５個である。
（２） 求める平面（または球面）の片側に３点、反対側に２点の配置になっている場合
ＡＢ−ＣＤＥ のとき、
明らかに、３点Ｃ、Ｄ、Ｅを通る直線（または円）がただ一つ存在する。
３点Ｃ、Ｄ、Ｅが同一直線上にあるとき、上記の問題の（２）と同様にして、５点から等
距離にある平面がただ1つ存在する。
３点Ｃ、Ｄ、Ｅが同一円周上にあるとき、△ＣＤＥの外接円の中心を通る垂線を Ｌ とお
き、線分ＡＢの中点を通り、線分ＡＢに垂直な平面を α とおく。
（イ） 垂線 Ｌ と平面 α が交わる場合、その交点を Ｏ とすると、Ｏ を中心として、５点
から等距離にある球面がただ1つ存在する。
（ロ） 垂線 Ｌ と平面 α が平行な場合、２点Ａ、Ｂは、３点Ｃ、Ｄ、Ｅを通る平面から等
距離にある。このとき、明らかに、５点から等距離にある平面がただ1つ存在する。
よって、この場合は何れにしても５点から等距離にある平面（または球面）がただ1つ存
在する。
５点から２点を選ぶ他の場合も同様である。
よって、平面（または球面）の個数は、５個から２個取る組合せの数 5Ｃ2＝１０（個）だけ
存在する。
以上から、求める平面（または球面）の個数は、 ５＋１０＝１５（個） である。
さらに、想像することが楽しくなるような次の問題を考えよう。
空間において、４つの平面があり、これらの交線により三角錐が出来るものとする。
このとき、４つの平面のすべてから等距離にある点は最大で幾つ存在するか？
答えは、８個だが、頭がパニックになりそうですね！
以下、工事中