ヨセフスの問題 
当HPがいつもお世話になっている未菜実さんから、「継子立ての問題」の話題をいただい
たので、少しこのことについてまとめてみたいと思う。
塵劫記(1630年頃)にある継子立ては、後妻の子である実子15人、先妻の子である継子15
人から家督を継ぐ1人を決めるとき、実子に後を継がせたいと思った継母(後妻で実子の親)
が策略を練って、
2、1、3、5、2、2、4、1、1、3、1、2、2、1
と交互に実子(●)と継子(●)を円形に並べ、
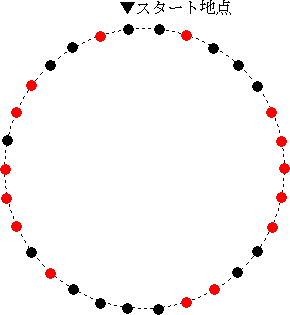
最初のスタート地点から数えて10人目ごとに外して、継子だけを除こうとした。
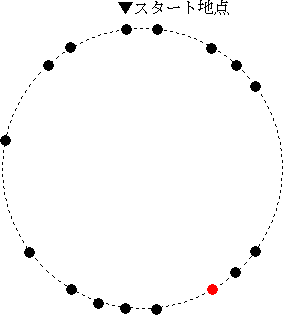
ここで、最後に残った継子が、「最後に残った私から数え始めてください。」と機転を利かした
結果、実子の人数の多さに油断して大どんでん返しにあい、継母の目論見はあっけなく崩れ
去ったという話でした。(文章中に差別的な表現がありますが、ご容赦下さい。)
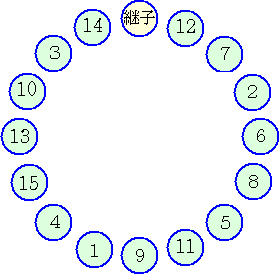
確かに、実子15人、継子1人の場合、継子から始めて10人おきに除いていくと、出発点
の人(継子)が残ることが分かる。(円内の数字は取り除かれていく順番を表す)
このように何人かを円形に並べて、ある人から数えて10人目の人を次々に除いていき、
最後に残る人が数え始めの人になるのは、最初の人数が10人以上の場合、16人、22
人、71人、・・・ の場合であることが知られている。
因みに、数え直しをして逆転が起こる最小の人数は15人ずつの計30人の場合である。
一般に、円形に並んだ人から一定の順番の人を次々に除いていき、最後に残った人を
考える問題を、西洋では、ヨセフスの問題 (370年頃ヘゲシッパスの名で書かれた物語
が起源といわれる)と呼ぶらしい。
※ フラウィウス・ヨセフス(37頃〜100頃)は歴史家として知られ、『ユダヤ戦記』を著した。このときの実話
を基にして作られた話と言われている。
ヨセフスの問題は、答えを出すだけだったら簡単である。裏表のあるオセロの駒などを
用意し、全て白にして円形に並べる。出発点を決めて、一定の順番毎に順次裏返してい
けばよい。
例 トランプ13枚が裏返しに束ねられている。いま、一番上のカードを最下段に移して、
次をめくり、机に置く。また上にあるカードを最下段に移して、次をめくり、先ほど置か
れたカードの右横に置く。このような操作を順次繰り返して、次々に机に並べていく。
このとき、並べられたカードが、左側から順番に、A、2、3、・・・、10、J、Q、K とな
るためには、最初に束ねられていたカードは上からどういう順番に並んでいたのだろ
うか?
答えは、7、A、Q、2、8、3、J、4、9、5、K、6、10 である。
これは、N個のものを円形に並べて、M個ずつ除いていくというヨセフスの問題のN=13、M=2
の特別な場合である。
未菜実さんは、「継子立て」で、N人をM人目ごとに取り除いていった場合の最後の1人をNとMを使って
どのように表すかという問題を考えておられる。最後に残る位置に規則性が見出せないとのことである。
西洋のヨセフスの問題に対して、塵劫記にある継子立ては、途中に数え直しがあり、ヨセ
フスの問題とは趣を異にしている。ちょっとだけ日本のものの方が難度が高いかなと思う。
この「継子立ての問題」は、古くから知られているようで、1100年頃の作と言われる。一
説には藤原通憲(みちのり 1106-1159)が考えたともいわれるが、詳細は不明らしい。
塵劫記より以前の「徒然草」(吉田兼好 1330年頃)の第137段「花は盛りに」に継子立
ての話題が取り上げられている。
因みに、徒然草の要旨を抜粋してみると・・・。
行き交う人たちを眺めていると、見覚えのある人がいかに多いかに気づく。そして、この世にはそれほど多くの
人がいるわけではない、私が死ぬのはこの人たちがみんな死んだ後としても、死を待つ時間はわずかであると
いうことを私は知った。。都に暮らす人は多いが、人が死なない日はない。死は、思いがけずやってくる。人生
は長いなどと悠長に構えていてはいけない。人が死んでいくのは、継子立てという遊びに似ている。最初はど
の石が除かれるか分からないが、次々に順番に取り除かれていくと、結局はどの石も逃れることはできない。
徒然草というと、「つれづれなるままに、日ぐらし硯にむかひて、心にうつりゆくよしなしごと
を、そこはかとなく書きつくれば、あやしうこそものぐるほしけれ。」という序段が有名である。
「心にうつりゆくよしなしごと」の例えに数学の話題を取り上げた吉田兼好の学識の深さに感
嘆させられる。
未菜実さんのHP「数理パズル」を覗いたら、次のような問題が載っていた。
ある余興で抽選会を行いました。円周上に1〜8まで番号が順番に振ってあります。
抽選箱の中には10から20までの番号を振った紙が入っており、一枚、主催者が引き、
「ままこだて」の要領で1番から右回りに数え始め、引いた番号ごとに数字を消してい
き、最後に残った番号に賭けた人で商品を山分けすることになりました。
さあ、あなただったら何番に賭けますか?そして、その確率は?
私の計算によれば、7番に賭けるのがベストかな?この場合の確率は、5/11 でした。
また、4番の確率が、2/11。2、3、5、8番の確率が、1/11 でした。意外にも、出発点の
1番と6番は、確率が、0 でした。未菜実さんは、「答えは意外!(^_-)」と仰っていますが、
何が意外なのでしょうか?ちょっと聞いてみたいですね!
さて、いよいよ本題に入ろう。
N人を円形に並べて、あるところから時計回りに順に、1、2、3、・・・、N と番号をつける。
番号1から時計回りに数え始め、M人目の人をその位置から取り除くことにする。取り除か
れた次の人から時計回りに数え始め、M人目の人をその位置から取り除く。このような操
作を繰り返して、最後に残る人が何番であるかを求めたい。
n人が円形に並んでいて、ある人から数え始めて、時計回りに上記の操作を繰り返したと
き、最後に残る人は数え始めの人から時計回りに数えて、A(n)番目とする。
すなわち、番号1から時計回りに数え始めて、A(N)番目の人が最後に残る。
いま、番号1から時計回りに数え始め、M人目の人をその位置から取り除いたとする。
すると、N−1人が円形に並んでいて、取り除かれた次の人(P)から時計回りに数え始め、
上記の操作を繰り返したとき、最後に残る人は、Pから時計回りに数えて、A(N−1)番目
になる。
したがって、漸化式 A(n)=M+A(n−1) が成り立つ。もちろん、A(1)=1 である。
このとき、最後に残る番号Kは、
K=Mod(A(N)−1,N)+1
ただし、A(n)=M+A(n−1) (2≦n≦N) 、A(1)=1
で与えられる。ただし、Mod(a,b)は、a を b で割った余りを表す。
この漸化式を、N=8、M=10 の場合に適用してみよう。
| n |
Mod(M−1+A(n−1),n)+1 |
Mod(A(n)−1,n)+1 |
| 1 |
|
1 |
| 2 |
Mod(9+1,2)+1 |
1 |
| 3 |
Mod(9+1,3)+1 |
2 |
| 4 |
Mod(9+2,4)+1 |
4 |
| 5 |
Mod(9+4,5)+1 |
4 |
| 6 |
Mod(9+4,6)+1 |
2 |
| 7 |
Mod(9+2,7)+1 |
5 |
| 8 |
Mod(9+5,8)+1 |
7 |
したがって、未菜実さんの問題で、主催者が引いた番号が10のとき、番号7が最後に残
ることが計算で確認された。
このような再帰的な計算は、表計算ソフト Excel の VBA にやらせるのが一番だろう。
プログラムは次の通りである。
Function a(n,m)
If n=1 Then
a=1
Else
a=(m−1+a(n−1,m)) Mod n +1
End If
End Function
Excel を起動し、[ツール]−[マクロ]−[Visual Basic Editor] とクリックして
Editor
を起動し、[挿入]−[標準モジュール] を選択して、上記を記述すればよい。
後は、Excelの任意のセルに、例えば、 =a(8,10) と打ち込むと、瞬時に、7
と最後に残る番号が得られる。
この関数を用いて、Excel上で、Nを連続的に変化させると(Mは10に固定)
最後に残る人が数え始めの人になるのは、最初の人数が、
1、2、16、22、71、227、528、1227、・・・
の場合であることが容易に確認される。
(追記) 当HPで活躍されている菅ちゃんから、「継子立て」についてご寄稿いただいた。
「継子立て」については古語辞書や国語便覧にも掲載されているが、国語の授業におい
ては、古文読解のために必要な、当時の習慣や価値観を教える必要があり、そのために
「継子立て」という遊びについても、「当時のこどもはこういう遊びをしていたのだ」と説明は
している。ただ、簡単にルールを説明して理解してもらえたら、すぐに本文に戻って講読を
進める形になってしまう。というのも、古文読解力の養成が主眼であって、継子立てという
遊戯そのものを研究することが目的ではないからである。一応、古文の授業で説明する程
度のことを述べることにする。
「継子立て」とは碁石を使う遊戯で、名称の由来は、白を先妻の子、黒を後妻の子に見
立て、相続人一人を決定するドラマに擬して遊んだことによる。「継子立て」の「立て」とは
「際立たせる」という意味からきているというのが定説である。
「継子立て」のゲーム内容は、黒白各15個ずつ合計30個の石を一定の順序で配列し
て円形もしくは方形に並べ、その中の一つを起点にして10番目に該当する石を取り除き、
以降、順次10番目の石を取り除いて、最後に残った石を勝ちとするルールである。
石の配列方法を工夫することで、特定の石が最後に残る(つまり勝ちになる)ように仕組
むことができる。さらに、途中で数え直しすることで、逆転現象が起こることが、このゲー
ムの特徴になっている。
白い石1個と黒い石15個が残った段階で、今度は白い石を起点にして10番目の石を
取り除いていく作業を繰り返すと、今度は黒い石が全て取り除かれ、最後に白い石1つ
だけが残る。継子立てに関する記述は『塵劫記』の他、それよりはるか以前に成立した
『二中暦』、『簾中抄』にも見られる。
徒然草は私の卒業論文のテーマにした作品。じっくり読んだので137段も当然知ってい
る。この文中に、
「継子立てと言ふものを双六の石にて作りて、立て並べたるほどは、取られん事いづれ
の石とも知らねども、数へ当てて一つを取りぬれば、その外は遁れぬと見れど、またまた
数ふれば、かれこれ間抜き行くほどに、いづれも遁れざるに似たり。」とあり、「人間は誰
でもいつかは必ず死がやってくる」ということの比喩として、継子立てを例示している。
授業で「継子立て」を説明する場合、机に碁石を並べても、後ろの座席に座っている生
徒には見えないので、●と○を描いて板書してから10番目のものを数えながら黒板消し
で一つずつ消したりなどしている。ただ、なぜ30個の石でやると逆転現象が起こるのか?
なぜ10番目の石を取り除くとそうなるのか?という理由までは数学的現象なので説明は
していない。
しかし、「継子立て」も考えてみれば不思議なものである。なぜ10番目の石を取り除かな
ければならないのか?5番目の石や2番目の石ではだめなのか?それに最初に白黒15
個ずつという設定も、たとえば17個ずつ34個の石では成立しないというのも不思議である。
30個の石と10番目を取り除く ・・・・ この数のもつ意味はやはり数学の分野ですね。
(追記) 上記では、N人を円形に並べて、ある番号から時計回りに数え始め、M人目の人
を順に、その位置から取り除いていったとき、最後に残る人が何番であるかについ
て考え、漸化式を求めて、実際にプログラムを組んだりもした。
ここでは、特に、M=2 の場合を取り上げ、その考察を行いたいと思う。
問題設定 N人を円形に並べて、あるところから時計回りに順に、1、2、3、・・・、N と番
号をつける。番号1から時計回りに数え始め、2人目の人をその位置から取り
除くことにする。取り除かれた次の人から時計回りに数え始め、2人目の人をそ
の位置から取り除く。このような操作を繰り返して、最後に残る人が何番である
かを求めよ。
例えば、N=10 の場合を実際に行ってみよう。
(下記で数字が一直線上に並んでいるが、左端と右端は線で結ばれ円形に並んでいるものと考えて下さい!)
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| ○ |
× |
○ |
|
|
|
|
|
|
|
| |
|
○ |
× |
○ |
|
|
|
|
|
| |
|
|
|
○ |
× |
○ |
|
|
|
| |
|
|
|
|
|
○ |
× |
○ |
|
| ○ |
|
|
|
|
|
|
|
○ |
× |
| ○ |
|
× |
|
○ |
|
|
|
|
|
| |
|
|
|
○ |
|
× |
|
○ |
|
| × |
|
|
|
○ |
|
|
|
○ |
|
| |
|
|
|
○ |
|
|
|
× |
|
| |
|
|
|
○ |
|
|
|
|
|
上記の手順から、最後に残る番号は、5番であることが分かる。
いま、番号1から始めて、最後に残る人の番号を、F(N) とおくと、上記より、F(10)=5
となる。N=1、2、3、・・・・、9 についても同様に計算すると、
F(1)=1 、F(2)=1 、F(3)=3 、F(4)=1 、F(5)=3 、F(6)=5 、F(7)=7
F(8)=1 、F(9)=3
となる。
これらをじっと眺めていると、あまりに不規則で規則性がないように感じられるが、実は
非常に美しい法則のあることが簡単に確かめられる。
番号 1、2、3、・・・、2n の 2n 人が円形に並んでいる場合、一周して残っている番号
は、1、3、5、・・・、2n−1 の n 人である。このとき、F(N) の定義から、最後に残る人
の番号は、上の数列のF(n)番目なので、2F(n)−1 である。
よって、 F(2n)=2F(n)−1 が成り立つ。同様に、
番号 1、2、3、・・・、2n+1 の 2n+1 人が円形に並んでいる場合、一周して残って
いる番号は、3、5、・・・、2n+1 の n 人である。このとき、F(N)
の定義から、最後に
残る人の番号は、上の数列のF(n)番目なので、2F(n)+1 である。
よって、 F(2n+1)=2F(n)+1 が成り立つ。
この漸化式を用いると、例えば、20人いた場合は、F(20)=2F(10)−1=9
より、
9番の人の残ることが簡単に求められる。
漸化式は、さらに、次のような変換公式をも生み出す。
N=an2n+an-12n-1+・・・+a12+a0 (an≠0) のとき、
F(N)=bn2n+bn-12n-1+・・・+b12+b0
ただし、 ak=1 のとき、 bk=1
ak=0 のとき、 bk=−1 (k=0、1、2、・・・、n)
(略証) n に関する帰納法で示される。
n=0 のとき、 N=a0=1 より、左辺=F(N)=F(1)=1 、右辺=b0=1 なので、
n=0 のとき成り立つ。
n=k (k≧0)のとき成り立つと仮定する。すなわち、
F(ak2k+ak-12k-1+・・・+a12+a0)=bk2k+bk-12k-1+・・・+b12+b0
n=k+1 のとき、N=ak+12k+1+ak2k+・・・+a12+a0 において、
a0=0 のとき、N=2(ak+12k+ak2k-1+・・・+a1) は偶数なので、
F(N)=2F(ak+12k+ak2k-1+・・・+a1)−1
=2(bk+12k+bk2k-1+・・・+b1)−1 =bk+12k+1+bk2k+・・・+b1+b0
a0=1 のとき、N=2(ak+12k+ak2k-1+・・・+a1)+1 は奇数なので、
F(N)=2F(ak+12k+ak2k-1+・・・+a1)+1
=2(bk+12k+bk2k-1+・・・+b1)+1=bk+12k+1+bk2k+・・・+b1+b0
となるので、n=k+1 のときも成り立つ。
よって、全ての n に対して、与式が成り立つ。 (証終)
例 20=1・24+0・23+1・22+0・2+0 なので、
F(20)=1・24−1・23+1・22−1・2−1=16−8+4−2−1=9 となる。
(コメント) 2進法展開というと、あまり馴染みが薄いが、このような使い方を知ると、俄然
その表記方法の特性が光り輝いて見える。とても素晴らしい変換公式だ!
Dengan kesaktian Indukmu さんからのコメントです。(令和3年8月21日付け)
上記において、
問題設定 N人を円形に並べて、あるところから時計回りに順に、1、2、3、・・・、N と番
号をつける。番号1から時計回りに数え始め、2人目の人をその位置から取り
除くことにする。取り除かれた次の人から時計回りに数え始め、2人目の人をそ
の位置から取り除く。このような操作を繰り返して、最後に残る人が何番である
かを求めよ。
が考察されている。もしも誰かに、Nについての具体的な数値付きでこの問題の解を求めよ
と問われたときにどうするかの簡便法があることを、知人から教わりましたのでご紹介したく
存じます。
たとえば、N=20のときには…… 上記では、
20=1・24+0・23+1・22+0・2+0 なので、
F(20)=1・24−1・23+1・22−1・2−1=16−8+4−2−1=9
と計算して求めていますが、もっと簡便に、
20の2進数表現を1ビットだけ巡回左シフトすれば、答えを得られます。
20=10100(2) なので、これをローテートして、 01001(2)=9 となります。これが解です。
(コメント) N=9=1001(2) を、1ビットだけ巡回左シフトすれば、0011(2)=3 で、確
かに、これが解となる。不思議な計算ですね!
この見方で、
20=1・24+0・23+1・22+0・2+0 なので、
F(20)=1・24−1・23+1・22−1・2−1=16−8+4−2−1=9
を再度考慮すると、
20=10100(2) に対して、
F(20)=1・24−1・23+1・22−1・2−1=1・23+1・2−1=1・23+1=1001(2)=9
となり、実は同じ計算をしているんですね。
(参考文献: ローレン・C・ラーソン 著 秋山 仁 ・飯田博和 訳
数学発想ゼミナール1 (シュプリンガー・フェアラーク))
(補足) 平成19年8月27日付け
上記の漸化式に関連する問題が、平成19年度入試 鳥取大学医学部 で出題された。
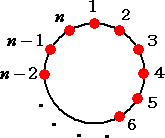
1 から n までの数字が 1 つずつ書かれた n 枚のカードを
右の図のように円周上に時計回りに並べる。
2 が書かれたカードから始めて時計回りに 1 枚おきにカー
ドを取り除く操作を続けていき、カードが最後の 1 枚になるま
で円周上を何回でも回る。そして残った 1 枚のカードに書か
れた数を F(n)とする。
ただし、 1 枚おきに取り除く操作は、まだ円周上に残ってい
るカードに対して行う。 |
 |
(1) 2 から 8 までの n に対し、F(n)の値を求めよ。
(2) 自然数 n に対して、 F(2n)=2F(n)−1 、F(2n+1)=2F(n)+1 が成り立つ
ことを示せ。
(3) 自然数 n に対して、F(2n)=1 が成り立つことを示せ。
(4) F(210+29+28+・・・+2+1)の値を求めよ。
問題の文章が少し分かりにくい...。
「1から時計回りに数え始め、2人目の人をその位置から取り除く。取り除かれた次の人か
ら時計回りに数え始め、2人目の人をその位置から取り除く。このような操作を繰り返す。」
と解釈できるかが、まず問題解法の糸口だろう。
(略解)(1)は、F(2)=1、F(3)=3、F(4)=1、F(5)=3、F(6)=5、F(7)=7、F(8)=1
(2)は、上記で証明した通りである。
(3)は、数学的帰納法による。
n=1 のとき、F(2)=1 より成り立つ。
n=k(k≧1)のとき成り立つと仮定する。すなわち、 F(2k)=1
n=k+1 のとき、 F(2k+1)=F(2・2k)=2F(2k)−1=1
よって、n=k+1 のときも成り立つ。
したがって、すべての自然数 n に対して、 F(2n)=1
(4)は、(2)を繰り返し用いて得られる。 すなわち、
F(210+29+28+・・・+2+1)
=F(2(29+28+・・・+2+1)+1)
=2F(29+28+・・・+2+1)+1
=・・・・・・・・・・・・・・・・・・・・・・・
=29F(2+1)+28+・・・+2+1
=210+29+28+・・・+2+1
=211−1
=2047 (略解終)
(コメント) 上記の公式を知っていれば、
F(210+29+28+・・・+2+1)=210+29+28+・・・+2+1
から直ちに答が導けるだろう。
(追記) 「継子立て」を用いて特定の集団を合法的に排除するためには、排除する集団を
非合法的に並べなければならないところが「継子立て」の弱点である。
最近、ある書籍で「継子立て」の並べ方を、言葉になぞらえて覚える方法があることを知
ったので、紹介したい。
例 白石 15個、黒石 15個を円形に並べる。ある白石から時計回りに数え始め、9番目
の石を取り除く。取り除かれた次の石から時計回りに数え始め、9番目の石を取り除
く。このような操作を繰り返して、黒石だけを取り除くようにしたい。最初に、どのように
並べたらいいのだろうか?
この答えは、時計回りに、
白4、黒5、白2、黒1、白3、黒1、白1、黒2、白2、黒3、白1、黒2、白2、黒1
と並べればよい。実際にやってみると、白から始めて順次黒のみが取り除かれる。
その覚え方は、個数に注目して、
1は、ア段の音、2は、イ段の音、3は、ウ段の音、4は、エ段の音、5は、オ段の音
とするといいそうだ。適当に意味がある言葉を続けるようにして、次のように作ってみた。
て の ち か く は さ き に つ か み し か
(手の近くは、先に掴みしか!)
(コメント) これで本当に覚えられるかしら?
(追記) ヨセフスの問題に関連して、当HPがいつもお世話になっているHN「GAI」さんが考
察されました。(平成25年2月25日付け)
黒石● 15個、白石○ 15個 計30個を円形に並べる。最初黒石のみを除外できる配列
のパターンを調べた。(◎は最後まで残る石の番号)
「k」はいくつ進んで石を取っていくかを表す。(1から数え始めます。)
(「継子立て」は、k=10 の場合。暗記方法では、k=9 の場合が取り上げられていますネ!)
k 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
29 30
2 ○ ● ○ ● ○ ● ○ ● ○ ● ○ ● ○ ● ○ ● ○ ● ○ ● ○
● ○ ● ○ ● ○ ● ◎ ●
3 ○ ○ ● ● ○ ● ○ ● ● ○ ○ ● ● ○ ● ○ ● ● ○ ○ ●
● ○ ● ○ ○ ● ○ ◎ ●
4 ○ ● ○ ● ● ◎ ● ● ○ ○ ● ● ● ○ ○ ● ○ ● ○ ● ○
○ ● ● ○ ○ ○ ● ● ○
5 ● ● ◎ ○ ● ● ○ ● ○ ● ○ ● ○ ○ ● ● ○ ● ○ ● ○
○ ● ● ● ○ ○ ○ ○ ●
6 ○ ● ○ ◎ ● ● ● ○ ○ ○ ● ● ○ ● ● ○ ○ ● ○ ○ ●
● ● ● ○ ○ ○ ● ○ ●
7 ● ○ ○ ○ ● ○ ● ● ● ○ ○ ● ● ● ○ ○ ○ ● ● ○ ●
● ◎ ○ ○ ○ ● ● ○ ●
8 ◎ ● ● ○ ● ○ ○ ● ● ○ ● ● ○ ○ ○ ● ○ ● ● ● ○
○ ● ● ○ ○ ○ ○ ● ●
9 ○ ○ ○ ○ ● ● ● ● ● ○ ○ ● ○ ○ ○ ● ○ ● ● ○ ◎
● ● ● ○ ● ● ○ ○ ●
10 ○ ○ ● ○ ○ ○ ● ● ● ● ● ○ ○ ● ● ○ ○ ○ ○ ● ○ ● ● ● ○ ● ● ◎ ○ ●
11 ○ ● ● ○ ● ● ○ ● ● ○ ● ○ ○ ● ● ○ ○ ○ ○ ● ● ● ● ○ ○ ● ● ◎ ○ ○
12 ● ● ● ◎ ● ● ○ ○ ○ ○ ● ● ○ ○ ● ● ○ ● ● ○ ○ ○ ● ● ● ○ ○ ○ ○ ●
13 ○ ○ ○ ○ ○ ● ● ● ● ○ ○ ● ● ○ ● ○ ○ ● ○ ● ○ ● ● ◎ ● ● ○ ○ ● ●
14 ○ ● ○ ● ● ○ ○ ● ○ ● ○ ● ● ● ○ ● ● ○ ○ ○ ○ ● ● ○ ○ ◎ ● ● ○ ●
15 ○ ● ● ◎ ○ ● ○ ○ ● ○ ○ ● ○ ○ ● ● ○ ● ● ○ ● ● ○ ● ○ ● ○ ○ ● ●
16 ● ● ○ ○ ● ● ◎ ○ ○ ○ ○ ● ● ● ● ● ○ ● ● ○ ○ ● ● ● ○ ○ ○ ● ○ ○
17 ● ○ ● ● ● ● ● ○ ● ● ○ ● ○ ○ ○ ● ● ○ ● ○ ○ ● ○ ● ○ ◎ ○ ○ ● ○
18 ○ ○ ● ● ○ ● ◎ ○ ○ ● ○ ○ ○ ● ○ ○ ● ● ○ ● ● ● ● ○ ● ● ● ● ○ ○
19 ○ ● ○ ○ ○ ● ● ● ● ● ● ○ ● ● ○ ○ ● ● ● ● ○ ○ ○ ○ ● ○ ◎ ● ○ ○
20 ● ● ● ○ ○ ○ ● ● ○ ● ○ ○ ○ ○ ● ○ ○ ○ ○ ● ● ● ● ● ● ◎ ● ● ○ ○
21 ○ ○ ● ● ● ● ● ○ ● ● ○ ● ○ ● ● ○ ○ ○ ● ● ● ○ ○ ◎ ○ ● ● ○ ○ ○
22 ● ○ ○ ○ ○ ● ● ○ ○ ○ ○ ○ ● ● ● ● ● ● ○ ● ● ● ○ ○ ● ● ◎ ○ ○ ●
23 ● ○ ○ ● ● ○ ○ ● ● ● ○ ○ ○ ○ ● ● ○ ○ ○ ○ ○ ● ● ◎ ● ● ● ● ○ ●
24 ○ ○ ● ● ● ● ◎ ● ● ○ ○ ● ● ○ ● ○ ● ● ○ ○ ○ ○ ● ● ○ ○ ● ○ ○ ●
25 ○ ● ○ ○ ○ ● ○ ○ ○ ● ● ● ● ○ ● ● ○ ● ● ● ● ◎ ○ ● ● ○ ○ ○ ○ ●
26 ○ ○ ◎ ○ ● ● ○ ○ ○ ○ ● ○ ○ ○ ○ ● ● ● ● ● ● ● ○ ● ● ● ○ ○ ○ ●
27 ● ○ ○ ● ○ ○ ○ ● ● ● ○ ○ ○ ○ ● ○ ○ ○ ● ◎ ● ● ● ● ○ ● ● ● ○ ●
28 ◎ ○ ● ○ ○ ○ ● ○ ● ● ○ ● ○ ○ ○ ○ ● ● ○ ○ ● ○ ○ ● ● ● ● ● ● ●
29 ○ ● ○ ○ ● ○ ○ ● ● ● ● ○ ○ ● ○ ● ○ ○ ○ ● ○ ● ○ ● ◎ ○ ● ● ● ●
30 ● ○ ● ● ○ ● ● ○ ○ ● ● ○ ● ○ ● ○ ○ ○ ○ ○ ● ● ● ○ ○ ○ ● ● ◎ ●
GAI さんからの続報です。(平成25年2月25日付け)
Akは、n個(1〜30)の小石を円形に並べていたとき、k進んで小石を取り除いて行ったと
きに(ただし、最初は1の位置から数え始めてスタートする)、最後まで残る小石の位置の番
号を30成分を持つベクトル形式で表示したものである。
[例] A10の第8成分が7の意味は
小石が8個円形に並べられているとき、10進んでは小石を取り除いて行ったとき、最後
まで残っている小石が7番目に置いてあった小石となる。(ただし、最初に取る石は2番に
ある石となる。)
A2 = [1, 1, 3, 1, 3, 5, 7, 1, 3, 5, 7, 9, 11, 13, 15, 1, 3, 5, 7, 9, 11,
13, 15, 17, 19, 21, 23, 25, 27, 29]
A3 = [1, 2, 2, 1, 4, 1, 4, 7, 1, 4, 7, 10, 13, 2, 5, 8, 11, 14, 17, 20, 2, 5, 8, 11, 14, 17, 20, 23, 26, 29]
A4 = [1, 1, 2, 2, 1, 5, 2, 6, 1, 5, 9, 1, 5, 9, 13, 1, 5, 9, 13, 17, 21, 3, 7, 11, 15, 19, 23, 27, 2, 6]
A5 = [1, 2, 1, 2, 2, 1, 6, 3, 8, 3, 8, 1, 6, 11, 1, 6, 11, 16, 2, 7, 12, 17, 22, 3, 8, 13, 18, 23, 28, 3]
A6 = [1, 1, 1, 3, 4, 4, 3, 1, 7, 3, 9, 3, 9, 1, 7, 13, 2, 8, 14, 20, 5, 11, 17, 23, 4, 10, 16, 22, 28, 4]
A7 = [1, 2, 3, 2, 4, 5, 5, 4, 2, 9, 5, 12, 6, 13, 5, 12, 2, 9, 16, 3, 10, 17, 1, 8, 15, 22, 2, 9, 16, 23]
A8 = [1, 1, 3, 3, 1, 3, 4, 4, 3, 1, 9, 5, 13, 7, 15, 7, 15, 5, 13, 1, 9, 17, 2, 10, 18, 26, 7, 15, 23, 1]
A9 = [1, 2, 2, 3, 2, 5, 7, 8, 8, 7, 5, 2, 11, 6, 15, 8, 17, 8, 17, 6, 15, 2, 11, 20, 4, 13, 22, 3, 12, 21]
A10 =[1, 1, 2, 4, 4, 2, 5, 7, 8, 8, 7, 5, 2, 12, 7, 1, 11, 3, 13, 3, 13, 1, 11, 21, 6, 16, 26, 8, 18, 28]
A11 =[1, 2, 1, 4, 5, 4, 1, 4, 6, 7, 7, 6, 4, 1, 12, 7, 1, 12, 4, 15, 5, 16,
4, 15, 1, 12, 23, 6, 17, 28]
A12= [1, 1, 1, 1, 3, 3, 1, 5, 8, 10, 11, 11, 10, 8, 5, 1, 13, 7, 19, 11, 2, 14, 3, 15, 2, 14, 26, 10, 22, 4]
A13 =[1, 2, 3, 4, 2, 3, 2, 7, 2, 5, 7, 8, 8, 7, 5, 2, 15, 10, 4, 17, 9, 22,
12, 1, 14, 1, 14, 27, 11, 24]
A14= [1, 1, 3, 1, 5, 1, 1, 7, 3, 7,10, 12, 13, 13, 12, 10, 7, 3,17, 11, 4, 18, 9, 23, 12, 26, 13, 27, 12, 26]
A15 =[1, 2, 2, 1, 1, 4, 5, 4, 1, 6, 10, 1, 3, 4, 4, 3, 1, 16, 12, 7, 1, 16, 8, 23, 13, 2, 17, 4, 19, 4]
A16= [1, 1, 2, 2, 3, 1, 3, 3, 1, 7, 1, 5, 8, 10, 11, 11, 10, 8, 5, 1, 17, 11, 4, 20, 11, 1, 17, 5, 21, 7]
A17= [1, 2, 1, 2, 4, 3, 6, 7, 6, 3, 9, 2, 6, 9, 11, 12, 12, 11, 9, 6, 2, 19, 13, 6, 23, 14, 4, 21, 9, 26]
A18 =[1, 1, 1, 3, 1, 1, 5, 7, 7, 5, 1, 7, 12, 2, 5, 7, 8, 8, 7, 5, 2, 20,
15, 9, 2, 20, 11, 1, 19, 7]
A19= [1, 2, 3, 2, 1, 2, 7, 2, 3, 2, 10, 5, 11, 2, 6, 9, 11, 12, 12, 11, 9, 6, 2, 21, 15, 8, 27, 18, 8, 27]
A20= [1, 1, 3, 3, 3, 5, 4, 8, 1, 1, 10, 6, 13, 5, 10, 14, 17, 1, 2, 2, 1, 21, 18, 14, 9, 3, 23, 15, 6, 26]
A21= [1, 2, 2, 3, 4, 1, 1, 6, 9, 10, 9, 6, 1, 8, 14, 3, 7, 10, 12, 13, 13, 12, 10, 7, 3, 24, 18, 11, 3, 24]
A22= [1, 1, 2, 4, 1, 5, 6, 4, 8, 10, 10, 8, 4, 12, 4, 10, 15, 1, 4, 6, 7, 7, 6, 4, 1, 23, 18, 12, 5, 27]
A23 =[1, 2, 1, 4, 2, 1, 3, 2, 7,10, 11, 10, 7, 2,10, 1, 7,12, 16, 19, 21,
22, 22, 21, 19, 16, 12, 7, 1, 24]
A24= [1, 1, 1, 1, 5, 5, 1, 1, 7, 1, 3, 3, 1, 11, 5, 13, 3, 9, 14, 18, 21, 1, 2, 2, 1, 25, 22, 18, 13, 7]
A25= [1, 2, 3, 4, 4, 5, 2, 3, 1, 6, 9, 10, 9, 6, 1, 10, 1, 8, 14, 19, 2, 5, 7, 8, 8, 7, 5, 2, 27, 22]
A26= [1, 1, 3, 1, 2, 4, 2, 4, 3, 9, 2, 4, 4, 2, 13, 7, 16, 6, 13, 19, 3, 7, 10, 12, 13, 13, 12, 10, 7, 3]
A27= [1, 2, 2, 1, 3, 6, 5, 8, 8, 5, 10, 1, 2, 1, 13, 8, 1, 10, 18, 5, 11, 16, 20, 23, 25, 26, 26, 25, 23, 20]
A28= [1, 1, 2, 2, 5, 3, 3, 7, 8, 6, 1, 5, 7, 7, 5, 1, 12, 4, 13, 1, 8, 14, 19, 23, 1, 3, 4, 4, 3, 1]
A29 =[1, 2, 1, 2, 1, 6, 7, 4, 6, 5, 1, 6, 9, 10, 9, 6, 1, 12, 3, 12, 20, 5,
11, 16, 20, 23, 25, 26, 26, 25]
A30= [1, 1, 1, 3, 3, 3, 5, 3, 6, 6, 3, 9, 13, 1, 1, 15, 11, 5, 16, 6, 15, 1, 8, 14, 19, 23, 26, 28, 29, 29]
小石の総数がもっと多くなった場合の調査が、「整数列大辞典」にあります。
A2→A006257、A3→A054995、A4→A088333、A5→A181281、A7→A178853、A8→A109630
(追記) 「継子立ての変形バージョン」と題して、GAI さんからご投稿いただきました。
(令和3年5月5日付け)
江戸初期に編成された塵劫記に「継子立て」という問題で、
ある家には、先妻の子と継母の子が、それぞれ15人ずつ、計30人いた。跡取りを決めるた
め、継母が一計を案じた。
子供たちを環状に並べ、継母の子(席1にいるA)から右回りに数え、10番目に当たった子
供を除いていくと、先妻の子ばかりが除かれていった。最後の1人になった先妻の子が、「こ
こからは、私から左回りに数えてください」と抗議すると、今度は継母の子ばかりが除かれ、
抗議したその子だけが残り、めでたく跡取りとなった。
という記事が載せられている。
この現象が起こるためには、30人の席は時計回りに席を1〜30の番号を振るとき、
A:継母の子、B:先妻の子とした場合
[A,A,B,A,A,A,B,B,B,B,B,A,A,B,B,A,A,A,A,B,A,B,B,B,A,B,B,A,A,B]
の状態であることになる。
そこで、この問題を変形し、
30人の子供のうち、各10人ずつのA:実子、B:継子、C:養子が円環で並んでいる。
上の問題を真似て、
まず、席1の子から数え始め、時計回りの10番目の子に当たる子供を取り除いていくと、
Bの子ばかりが取り除かれていき、これでは最後のBの子供も除かれることになっていま
うので、最後にきたBが、「これではBばかりがのけられて不公平です。いまから私から数
え始め、10番目の人に変更して下さい。ただし時計回りの方向はそのままでいいです。」
皆も賛同したので、変更でのルールで取り除いていった。
すると、今度は、Cの子供ばかりが取り除かれることになり、最後のCは、これではAだけ
が残ってしまい、これでは不公平であると主張した。
そこで、最後のCはある提案をした。
「今度は私から数え始め、時計回りに x 番目の人を取り除いて下さい」
これで実施すれば、Aがどんどん取り除かれていき、残された3人の子供は、各A、B、Cの
人になったという。
この現象が起こせるためには、最後のCが提案した x の最小値はいくつか?
また、残される3人は最初の30人の時計回りの席1〜30のどこに座っていた人か?
スモークマンさんからのコメントです。(令和3年5月6日付け)
ただ地道に辿ってみただけですが...^^;
最後12人残った場合、5番目の人を除いていくと、3人(Cを1番目とすると、1,2,6番目)だけ
残るのですが...時計回りでは無理では?時計回りに -5 番目ずつ取り除くでもいいなら可能
で...
24番目がB 、28番目がC 、16番目がA
のとき...?
GAI さんからのコメントです。(令和3年5月7日付け)
最後12人残った場合、5番目の人を除いていくと、3人(Cを1番目とすると、1,2,6番目)だけ
残るのですが...時計回りでは無理では?
ここを4番目の人で除いて行けば、
24番目がB 、19番目がC 、13番目がA
の3人が残されるになりませんかね?もし、5番目なら、Aは2番目で残る。
(追記) 令和3年6月26日付け
今度は、継子立ての逆問題を考えてみよう。
12個の碁石を円形に並べて、次の要領で碁石を取り除く。Aの石から順に時計回りに数
えていき、7番目の石Gを取り除く。次に、Gの隣の石Hから時計回りに数えていき、7番目
の石を取り除く。
ある石から順にこのような手順を繰り返して石を取り除いていったところ、最後にFの石が
残ったという。
果たして、どの石から数え始めたのだろうか?
ただし、順番を数えるとき、取り除いた石は数えないものとする。
(解) Aという石から数え始めたとき残る石が何かを考えればよい。
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
| |
|
|
|
|
|
× |
|
|
|
|
|
| |
× |
|
|
|
|
|
|
|
× |
|
|
| |
|
|
|
|
× |
|
|
|
|
|
|
| |
|
|
× |
|
|
|
|
|
|
|
|
| |
|
× |
|
|
|
|
|
|
|
|
|
| |
|
|
|
× |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
× |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| × |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
× |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
× |
|
上図から、最後に残るのは、Lである。このことから逆算して、最後に残る石がFであるた
めには、碁石Gから数え始めればよいことが分かる。
(追記) 当HP読者のHN「K.N.」さんからのご投稿です。(令和5年6月12日付け)
漸化式について調べていたら、このページにたどり着き、楽しく拝見させていただきました。
学生だったころ、下記のような問題をだされて答えられなかったことを思い出しました。
あなたを含めて20名の人が海賊に捕まり、今、海賊船の甲板で輪になって立たされてい
る。海賊船には食料があまりないので、1名だけ残して、あとはサメの餌にします。あるとこ
ろから3ずつ数えていき、一人ずつ海に投げ入れます。あなたは、どこに立っていたら生き
残れるでしょうか。
最近、仕事で数学の教科書を見直す機会があり、漸化式を読んでいたら・・・これのことだっ
たのかと気づきました。そして、継子立てにたどり着き、MS-Excelで漸化式を作って答えを求
め、C#(Microsoftの開発環境Visual Studio C#)でも作りました。記憶のどこかに眠っていて
引っ掛かっていたことが明確になり、すっきりしました。感謝しております。
このページは、「以下、工事中!」になっており、まだ続編があると思われますが、継子立て
を理解し、自分でプログラムを作成したまではよいのですが、A(n) = M+A(n-1) の M が毎回
増える場合や一定値増えたり減ったりを繰り返す場合や、Mの数は一定でも回数を重ねるごと
に除く数が増えていく場合などは漸化式にできるのかどうか疑問が湧いてきました。
そのうち考えてみたいと思っております。まずは目先の仕事をこなしていきます。
(コメント) K.N.さん、当HPをご覧いただきありがとうございます。因みに、K.N.さんの
問題の答えは、数え始め地点からちょうど20人目にいれば、助かりますかね!
以下、工事中!




