球の軌跡の体積 　　　　　　　　　　　　　　　　　　　　　　　　　　　

　平成１８年９月６日付けで当ＨＰの掲示板「出会いの泉」に、当ＨＰがいつもお世話になっ
ている加俊さんから、加俊さん創作の、ある立体の求積の問題が提起された。

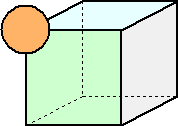一辺の長さ４の立方体の全ての辺上を半径１の球の 　　中心が移動する。 　　　このとき、その球の通過する部分の体積を求めよ。

　このときに作られる立体は、次のような雰囲気かな？

　　　　　　　　　　　　

　文房具に、絵の具をドライヤーなどで暖めると膨張するというものがある。そのような感
覚で、立方体の各辺が半径１だけ熱膨張したと考えてもいいだろう。

　この問題に対して、らすかるさんが、９月７日付けで解答を寄せられた。

　立体図形を組み合わせたり切ったりして、どんな形になるかを頭の中で想像するのは難
しく、形を把握するまで時間がかかったそうである。

　この問題の急所は、角の形状がどうなっているかを把握することだろう。

　らすかるさんは、次のように考えられたとのこと。

　　この図形の場合、まず「正方形の辺」上を「円」が移動することを考えると、想像しやす
いと思う。角に注目して、角の四分円を削除してから対称になるように分割すると、

　　　　　　　　　

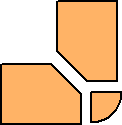
のようになるが、このうちの

　　　　　　　　　　　　　　

の部分だけを考えればよい。

　次に、これを「正方形の辺」と「球」で同じように考えれば、この部分は円柱を、片方の底
面の直径と他方の面の端を結び、底面と４５°の角度をなす平面で切った形になる。

　言葉では正確に書くのは難しいので、ｘｙｚ空間で表現すると、

　　ｘ²＋ｙ²≦１　、−１≦ｚ≦０ の円柱を平面 ｘ＝ｚ で切った下側の形

である。

　そして、これを「立方体の辺」と「球」で考えると、直角の別方向の平面でもう一度切った形、
すなわち

　　ｘ²＋ｙ²≦１　、−１≦ｚ≦０ の円柱を平面 ｘ＝ｚ で切った下側の形をさらに平面
ｙ＝ｚ で切った下側の形

となる。

　実際に、そのような図形を描画すれば下図のようなものである。

　　　　　　　　

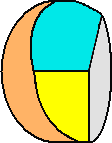
　　　　　（灰色の部分をどうしても表に出したかったので、ちょっと高さの部分が変かな？
　　　　　　図形をかなり鉛直方向に近い方から眺めているものと思ってください！
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　．．．ちょっと言い訳！ｆ(^^;)　）

　上記図形の体積は、底面が半径１の円で高さが１の円柱の体積から、下図の図形の体
積を２個分差し引いて得られる。

　　　　　　　

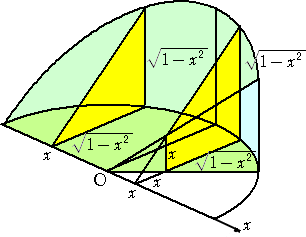
　上図の立体の体積計算は、高校「数学�V」で学ぶ。

実際に、
　　　　　

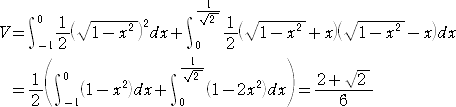
　　　　（らすかるさんは別な方法で計算しているが、ａｒｃｓｉｎ を用いないコチラの方が十分
　　　　高校生的だと思う。）

なので、
　　　　　　　　

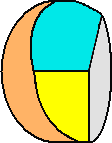
の体積は、
　　　　　　　　　

となる。

　求める立体の体積は、

　　　底面の半径１の円で高さが２の円柱が１２個分で、　π×２×１２＝２４π
　　　半径１の球の１/８が８個分で、　（４π/３）×（１/８）×８＝４π/３
　　　上図の立体が３×８＝２４個分で、　（π−（２＋）/３）×３×８＝２４π−１６−８

の和になる。すなわち、

　　　　　　

（コメント）　最初、どんな図形かを想像するのが難しくて、らすかるさんのヒントをもとに理解
　　　　　　できました。楽しい問題を提起していたいただいた加俊さん、そして鮮やかに解か
　　　　　　れたらすかるさんに感謝いたします。