
丂旕夞揮懱偺懱愊偼丄愗傝岥傪岻柇偵慖傇偲柺敀偄傛偆偵懱愊偑媮傔傜傟傞丅
椺丂曻暔慄 倄亖俁/係亅倃2 傪 倄幉偺廃傝偵夞揮偟偰偱偒傞棫懱傪丄俲 偲偍偔丅偙偺棫懱 俲 傪丄
丂丂夞揮幉偲 係俆亱傪側偡暯柺 俫 偱愗抐偟偨偲偒丄暯柺偺忋曽偺晹暘偺懱愊傪媮傔傛丅
丂乮搶嫗戝妛乯
丂倃倄倅嬻娫偵偍偄偰丄棫懱 俲 偼丄曽掱幃 倅亝俁/係亅倃2亅倄2 偱梌偊傜傟傞傕偺偲偟偰傛偄丅
夞揮懱偺懱愊 丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂旕夞揮懱偺懱愊偼丄愗傝岥傪岻柇偵慖傇偲柺敀偄傛偆偵懱愊偑媮傔傜傟傞丅
椺丂曻暔慄 倄亖俁/係亅倃2 傪 倄幉偺廃傝偵夞揮偟偰偱偒傞棫懱傪丄俲 偲偍偔丅偙偺棫懱 俲 傪丄
丂丂夞揮幉偲 係俆亱傪側偡暯柺 俫 偱愗抐偟偨偲偒丄暯柺偺忋曽偺晹暘偺懱愊傪媮傔傛丅
丂乮搶嫗戝妛乯
丂倃倄倅嬻娫偵偍偄偰丄棫懱 俲 偼丄曽掱幃 倅亝俁/係亅倃2亅倄2 偱梌偊傜傟傞傕偺偲偟偰傛偄丅
|
丂丂偙偺棫懱傪丄暯柺 俫 丗 倅亖倄 偱愗抐偡傞丅 丂丂偦偺寢壥偱偒傞棫懱偺偆偪丄暯柺 俫 偺忋曽 丂偵偁傞棫懱傪丄暯柺 倃 亖 倲丂偱愗偭偨偲偒偺愗 丂傝岥偺恾宍偼丄曽掱幃 丂丂丂丂丂倅亝亅倄2亄俁/係亅倲2丂乮偨偩偟丄倅亞倄乯 丂偲側傞丅乮壓恾乯 |
||
丂丂丂 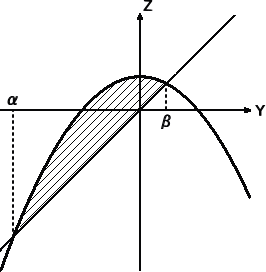 |
|||
丂兛亄兝亖亅侾丂丄兛兝亖倲2亅俁/係丂側偺偱丄
俽亖乮侾/俇乯乮兝亅兛乯3亖乮侾/俇乯乷乮兝亅兛乯2乸3/2
亖乮侾/俇乯乷乮兛亄兝乯2亅係兛兝乸3/2亖(係/俁)乮侾亅倲2乯3/2
偙偺偲偒丄媮傔傞懱愊 倁 偼丄
丂![]()
丂抲姺愊暘偵傛傝丄丂倁亖兾/俀丂偲側傞丅
丂偙偺傛偆側旕夞揮懱偺懱愊偵懳偟偰丄夞揮懱偺懱愊偺寁嶼偼丄柺敀傒偵寚偗傞偲偙傠偑
偁傞偑丄偦偺曽朄榑偵偼旝暘愊暘偺峫偊曽偺僄僢僙儞僗偑娷傑傟偰偄傞傕偺偲峫偊傜傟傞
偺偱丄偙偺儁乕僕偱惍棟偟偰偍偙偆偲巚偆丅
 |
丂 嵍恾偺傛偆偵丄嬋慄 倄亖倖乮倃乯 偑丄捈 |
|
| 偧傟 俵丄俵乫偲偍偔偲丄師偺晄摍幃偑惉傝棫偮丅 | ||
丂![]()
儮倶 仺 侽 偺偲偒丄俵丄俵乫 仺 俹俫 側偺偱丄
丂![]()
偲側傞丅偟偨偑偭偰丄媮傔傞懱愊 倁 偼丄師偺掕愊暘偵傛傝媮傔傜傟傞丅
丂![]()
| 丂丂丂乮 偙偙偱丄丂 | 丂 |
丂丂丆丂丂 | 丂丂偱偁傞丅乯 |
丂偙偺岞幃偼丄師偺傛偆偵峫偊偰傕摼傜傟傞丅 |
|
|
丂丂丂丂丂丂丂 |
丂偵偍偄偰丄 |
丂![]()
側偺偱丄
丂![]()
傛偭偰丄
丂![]()
偙偙偱丄
丂![]()
側偺偱丄
丂![]()
偑惉傝棫偮丅
乮拲堄乯丂俹俫亖俹俻們倧倱兤 側偺偱丄忋婰偺岞幃偼丄
丂![]()
偲傕彂偗傞丅
椺丂曻暔慄 倄亖倃2 偲捈慄 倄亖倃 偱埻傑傟偨晹暘傪捈慄偺廃傝偵夞揮偝偣偰偱偒傞棫懱偺
丂丂懱愊傪媮傔傛丅
丂媮傔傞懱愊 倁 偼丄
丂![]()
偲側傞丅
乮嶲峫乯丂忋婰偺椺偺栤戣偼丄嫵壢彂摍偱偼捠忢師偺傛偆偵夝偐傟偰偄傞丅
 |
丂丂丂嵍恾偵偍偄偰丄媮傔傞懱愊 倁 偼丄 丂丂丂丂 丂丂偙偙偱丄 丂丂丂丂 丂丂丂丂 丂丂側偺偱丄 丂丂丂丂丂丂丂丂丂 |
傛偭偰丄
丂![]()
丂撉幰偺偨傔偵丄楙廗栤戣傪巆偟偰偍偙偆丅
楙廗栤戣
 |
丂丂丂嵍恾偵偍偄偰丄俀嬋慄偱埻傑傟傞恾宍傪捈慄偺 丂丂廃傝偵夞揮偝偣偰偱偒傞棫懱偺懱愊傪媮傔傛丅 乮摎偼丄(俀/俁)(係俉俆亅俀俆俀倢倧倗俇) |
乮捛婰乯丂暯惉俀俆擭俋寧俋擔晅偗
丂宑滀媊弇戝妛丂棟岺乮俀侽侾俁乯丂偱偙偺僞僀僾偺栤戣偑弌戣偝傟偨丅宑滀傜偟偔丄寁嶼偑暋
嶨偵側傞傛偆偵堄幆揑偵栤戣偑嶌傜傟偰偄傞偲偙傠偑怱憺偄丅
丂曻暔慄 倷亖![]() /俀倶2 偲捈慄 倷亖倶 偱埻傑傟偨恾宍傪丄捈慄 倷亖倶 偺傑傢傝偵侾夞揮偟偰偱
/俀倶2 偲捈慄 倷亖倶 偱埻傑傟偨恾宍傪丄捈慄 倷亖倶 偺傑傢傝偵侾夞揮偟偰偱
偒傞棫懱偺懱愊倁傪媮傔偨偄丅
乮侾乯丂倰亞侽 偲偡傞丅捈慄 倷亖倶 忋偵偁傝尨揰俷偐傜偺嫍棧偑 倰 偲側傞揰偺偆偪丄倶 嵗昗偑侽
丂丂埲忋偺揰傪俹偲偡傞丅揰俹傪捠傝丄捈慄 倷亖倶 偵悅捈側捈慄傪俴偲偡傞偲丄俴偺曽掱幃偼
丂丂倷亖乮丂僀丂乯偲側傞丅傑偨丄曻暔慄 倷亖![]() /俀倶2 忋偵偁傞偺偼丄倰亖侽 偲 倰亖乮丂儘丂乯偺偲
/俀倶2 忋偵偁傞偺偼丄倰亖侽 偲 倰亖乮丂儘丂乯偺偲
丂丂偒偱偁傞丅
乮俀乯丂侽亝倰亝乮丂儘丂乯偲偟丄揰俹偲捈慄俴傪乮侾乯偺傛偆偵偲傞丅捈慄俴偲曻暔慄 倷亖![]() /俀倶2 偺
/俀倶2 偺
丂丂岎揰偺偆偪丄倶 嵗昗偑侽埲忋偺揰傪俻偲偡傞丅揰俹偲揰俻偺嫍棧俹俻偺俀忔傪 倰 傪梡偄偰
丂丂昞偡偲丄俹俻2亖乮丂僴丂乯偲側傞丅
乮俁乯丂媮傔傞棫懱偺懱愊倁偑丄倁亖兾佺0乮蹃j乮丂僴丂乯倓倰丂偲側傞偙偲傪梡偄偰丄倁傪媮傔側偝偄丅
乮棯夝乯丂乮侾乯丂倷亖亅倶亄![]() 倰丂丄倰亖俀丂丂乮俀乯丂倰2亄俇倰亄俀亅俀乮倰亄侾乯併乮係倰亄侾乯
倰丂丄倰亖俀丂丂乮俀乯丂倰2亄俇倰亄俀亅俀乮倰亄侾乯併乮係倰亄侾乯
丂丂丂乮俁乯丂兾/侾俆
乮捛婰乯丂暯惉俀俁擭侾俀寧侾侾擔晅偗
丂忋婰偺榖戣偵偮偄偰丄摉俫俹撉幰偺俫俶乽廫榋栭侓乿偝傫偐傜侾俀寧侾侽擔晅偗偱儊乕儖傪捀
偄偨丅
丂幬夞揮懱偺嶱宆暘妱偱丄乽愵宍偺柺愊亊d倶乿傪廤傔偰寁嶼偡傞偺偑晛捠傜偟偄偺偱偡偑丄
巹偼崅峑帪戙偐傜丄幬夞揮懱偺懱愊偼丄乽嶱宆暘妱仺墴偟偮傇偡乿曽幃偱寁嶼偟偰偄傑偟
偨丅
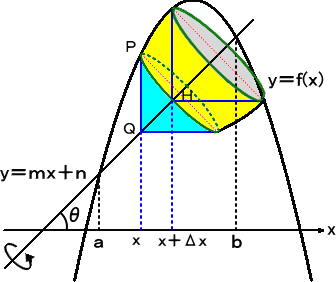 |
丂 |
丂墴偟偮傇偝傟偨墌拰 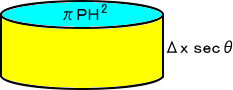 |
丂丂傛偭偰丄媮傔傞懱愊偼丄 丂丂 |
丂巹偺扵偟曽偑埆偄偺偐丄偦傟偲傕儅僀僫乕側峫偊曽側偺偐丄僱僢僩忋専嶕偟偰傕摨條偺寁
嶼曽朄偼側偐側偐尒偮偐傝傑偣傫丅
丂偙偺峫偊曽偼丄偍偦傜偔惓偟偄偲巚偆偺偱偡偑丄晛捠偺曽朄側偺偐丄偦傟偲傕偁傑傝傗傜側
偄傕偺側偺偐丄偤傂偛堄尒傪暦偐偣偰偔偩偝偄丅
乮僐儊儞僩乯丂寢榑偐傜尵偆偲丄傛偔抦傜傟偨晛捠偺曽朄偱偡丅悢妛揑偵偼丄
丂兾俹俫2丒儮倶倱倕們兤亖兾俹俫丒俹俫倱倕們兤丒儮倶亖兾俹俫丒俹俻丒儮倶
偲曄宍偟丄旝彫晹暘偺懱愊傪
丂乷乮愵宍偺屖挿乯亐俀乸亊乮愵宍偺敿宎乯亊乮岤傒乯亖乮愵宍偺柺愊乯亊乮岤傒乯
偲峫偊傞偺偑堦斒揑偱偡丅
丂乽廫榋栭侓乿偝傫偺峫偊曽偼丄偙偺棳傟偵増偭偨傕偺偱惓摑揑側夝朄偲尵偊傞偲巚偄傑偡丅
乮嶲峫暥專乯丂廐嶳丂恗丂挊丂乽棫懱偺偲傜偊偐偨乿丂乮弜戜暥屔乯
丂丂丂丂丂丂戞俀復丂棫懱偺懱愊偺媮傔曽丂倫丏俇侾乣倫丏侾侽俋
乮娬榖媥戣乯
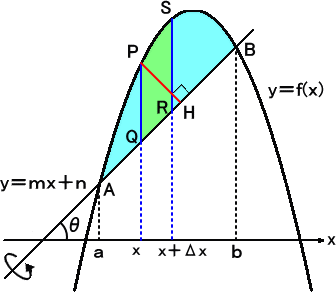
丂捈慄偺廃傝偺夞揮偼丄揔摉側嵗昗曄姺乮夞揮堏摦乯偵傛傝丄嵗昗幉偺廃傝偺夞揮偺栤戣
偵婣拝偝傟傞丅
丂師偺傛偆側栤戣偑丄傛偔抦傜傟偰偄傞丅
椺丂嬋慄 ![]() 丂偲奺嵗昗幉偱埻傑傟偨晹暘傪丄捈慄 y 亖 倶 偺廃傝偵夞揮偝偣偰
丂偲奺嵗昗幉偱埻傑傟偨晹暘傪丄捈慄 y 亖 倶 偺廃傝偵夞揮偝偣偰
丂丂偱偒傞棫懱偺懱愊傪媮傔傛丅乮偍拑偺悈彈巕戝妛乯
俫倝値倲丗丂俀嬋慄傪尨揰偺廃傝偵係俆亱夞揮偝偣偰峫偊傞丅嬋慄偺曽掱幃偼丄倃2亖![]() 倃亅(1/俀)
倃亅(1/俀)
丂偲側傞丅乮摎偼丄![]() 兾/係俉丂偐側丠乯
兾/係俉丂偐側丠乯
丂偙偺曽朄偼丄巹偑崅峑惗偺崰傛偔梡偄傜傟偨夝朄偱偁傞丅寁嶼偑斚嶨偡偓偰丄偁傑傝偍姪
傔偱偒側偄偑丄媮傔偨偄懱愊偑妋偐偵媮傑偭偰偄傞偲偄偆偙偲偑幚姶偱偒傞夝朄偱偁傞丅
乮嶲峫暥專丗扟岥丂彑丂挊丂旝暘丒愊暘丂乮墵暥幮乯
丂丂丂丂丂丂丂彫尨泬峎丂挊丂捈慄 倢 偺廃傝偺夞揮懱偺懱愊丂乮悢尋捠怣乯乯
乮捛婰乯丂暯惉俀侾擭俈寧侾擔晅偗
丂乽擬寣両暯惉嫵堢妛堾乿乮僼僕俿倁宯丂侾俋帪乣乯偺俇寧俀俉擔曻憲偱丄夞揮懱偺宍傪栤偆栤戣
偑弌戣偝傟偨丅
丂偪傚偭偲栚傪堷偔栤戣偩偭偨偺偱峫偊偰傒偨丅
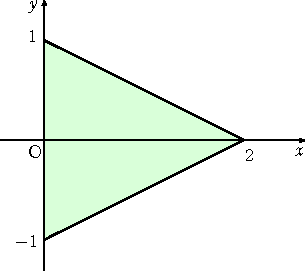 |
丂丂嵍恾偺傛偆側嶰妏宍傪傑偢丄倶 幉偺廃傝 丂偵夞揮偝偣丄偦偺偲偒弌棃傞恾宍傪丄偝傜 丂偵丄倷 幉偺廃傝偵夞揮偝偣傞丅 丂丂偙偺偲偒弌棃傞恾宍偼丄偳偺傛偆側宍偵 丂側傞偩傠偆偐丠 |
丂偙偺栤戣偼丄墌悕偺曣慄偐傜側傞嶰妏宍偲掙柺偺墌傪摨堦暯柺偵昤偄偰峫偊傞偲丄偳傫側
恾宍偵側傞偐偼梕堈偵梊憐偱偒傞偩傠偆丅
丂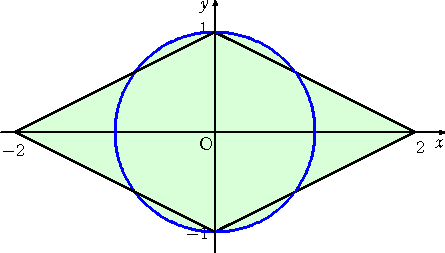
丂偙傫側姶偠偐側丠
丂
丂偙偺棫懱偺懱愊傪媮傔傞偙偲偼丄悢妛嘨偺庤崰側墘廗栤戣偵側傞偩傠偆丅
丂丂倶2亄倷2亖侾丂偲丂倶亄俀倷亅俀亖侽丂偺岎揰偺 倷 嵗昗偼丄侾丂傑偨偼丂俁/俆
傛偭偰丄
丂
偲側傞丅
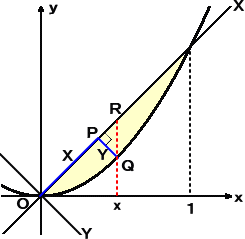
丂暯惉俀俈擭搙擖帋丂搶嫗戝妛慜婜棟宯偱師偺傛偆側夞揮懱偺懱愊偺栤戣偑弌戣偝傟偨丅
壗傕擄偟偄偲偙傠偼側偔嫵壢彂揑偱椙怱揑側弌戣偲尵偊傛偆丅
栤戣丂倎傪惓偺幚悢偲偟丄倫傪惓偺桳棟悢偲偡傞丅
丂丂丂嵗昗暯柺忋偺俀偮偺嬋慄 倷亖倎倶倫丂乮倶亜侽乯偲 倷亖倢倧倗 倶丂乮倶亜侽乯傪峫偊傞丅偙偺俀偮偺
丂丂嬋慄偺嫟桳揰偑侾揰偺傒偱偁傞偲偟丄偦偺嫟桳揰傪俻偲偡傞丅
埲壓偺栤偄偵摎偊傛丅昁梫偱偁傟偽丄倢倝倣倶仺亣 倶倫/倢倧倗 倶亖亣丂傪徹柧側偟偵梡偄偰傛偄丅
乮侾乯丂倎偍傛傃揰俻偺倶嵗昗傪倫傪梡偄偰昞偣丅
乮俀乯丂偙偺俀偮偺嬋慄偲倶幉偱埻傑傟傞恾宍傪丄倶幉偺傑傢傝偵侾夞揮偟偰偱偒傞棫懱偺懱愊傪
丂丂丂倫傪梡偄偰昞偣丅
乮俁乯丂乮俀乯偱摼傜傟傞棫懱偺懱愊偑俀兾偵側傞偲偒偺倫偺抣傪媮傔傛丅
乮夝乯乮侾乯丂嬋慄 倷亖倎倶倫丂乮倶亜侽乯偲 倷亖倢倧倗 倶丂乮倶亜侽乯偼偲傕偵憹壛娭悢偱丄慜幰偼壓偵撌丄
丂丂丂丂丂屻幰偼忋偵撌偺僌儔僼偱偁傞丅
傛偭偰丄戣堄傪枮偨偡偨傔偵偼丄嫟桳揰俻乮倲丆倎倲倫乯偱俀嬋慄偑愙偡傞偙偲偑昁梫廫暘偱偁傞丅
丂偟偨偑偭偰丄丂倎倲倫亖倢倧倗 倲丂丄丂倎倫倲倫-1亖侾/倲丂傛傝丄丂倫倢倧倗 倲亖侾丂偡側傢偪丄丂倲亖倕1/p
偙偺偲偒丄丂倎倕亖侾/倫丂傛傝丄丂倎亖侾/乮倕倫乯
乮俀乯丂倁亖兾佺0倕1/p 倎2倶2倫 倓倶亅兾佺1倕1/p (倢倧倗 倶)2倓倶
丂亖兾(倎2/(俀倫亄侾)乯[倶2倫+1]0倕1/p亅兾乮[倶(倢倧倗 倶)2]1倕1/p亅俀佺1倕1/p (倢倧倗 倶)倓倶乯
丂亖兾(倎2/(俀倫亄侾)乯倕(2倫+1)/p亅兾倕1/p(侾/倫)2亄俀兾乮[倶倢倧倗 倶]1倕1/p亅佺1倕1/p倓倶乯
丂亖兾(倎2/(俀倫亄侾)乯倕(2倫+1)/p亅兾倕1/p(侾/倫)2亄俀兾乮倕1/p(侾/倫)亅倕1/p亄侾乯
丂亖兾(倎2/(俀倫亄侾)乯倕(2倫+1)/p亅兾倕1/p乮(侾/倫)2亅俀/倫亄俀乯亄俀兾
偙偙偱丄丂倎亖侾/乮倕倫乯丂偱偁傞偺偱丄
倁亖兾(侾/(俀倫亄侾)倕2倫2乯倕(2倫+1)/p亅兾倕1/p乮(侾/倫)2亅俀/倫亄俀乯亄俀兾
亖兾(侾/(俀倫亄侾)倫2乯倕1/p亅兾倕1/p乮(侾/倫)2亅俀/倫亄俀乯亄俀兾
亖俀兾乷乮侾亅俀倫乯/乮侾亄俀倫乯乸倕1/p亄俀兾
乮俁乯丂戣堄傪枮偨偡偨傔偵偼丄丂侾亅俀倫亖侽丂偡側傢偪丄丂倫亖侾/俀
乮僐儊儞僩乯丂寁嶼偺曽恓偼偡偖棫偪傑偡偑丄偦傟傪幚峴偡傞寁嶼椡偑媮傔傜傟偰偄傑偡偹両
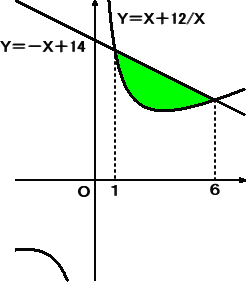
丂師偺搶杒戝妛丂棟宯乮侾俋俈俉乯偺栤戣傕丄夞揮懱偺懱愊偺栤戣偱偁傞丅
戞俆栤丂丂侽亝倲亝兾/俀 偲偡傞丅嬋慄 倷亖倱倝値 倶 偍傛傃俁捈慄 倶亖倲丄倶亖俀倲丄倷亖侽 偱埻傑傟偨
丂丂晹暘傪丄倶 幉偺傑傢傝偵夞揮偟偰摼傜傟傞棫懱偺懱愊傪倁乮倲乯偲偡傞丅倁乮倲乯偑嵟戝偵側傞
丂丂倲 偺抣傪兛偲偡傞偲偒丄們倧倱兛偺抣傪媮傔傛丅
乮夝乯丂倁乮倲乯亖兾佺倲2倲 倱倝値2倶倓倶亖乮兾/俀乯佺倲2倲 乮侾亅們倧倱俀倶乯倓倶亖乮兾/俀乯乵倶亅乮侾/俀乯倱倝値俀倶乶倲2倲
丂亖乮兾/俀乯乮倲亅乮侾/俀乯乮倱倝値係倲亅倱倝値俀倲乯乯丂傛傝丄
倁乫乮倲乯亖乮兾/俀乯乮侾亅乮俀們倧倱係倲亅們倧倱俀倲乯乯亖乮兾/俀乯乮侾亅乮俀乮俀們倧倱2俀倲亅侾乯亅們倧倱俀倲乯乯
亖亅乮兾/俀乯乮係們倧倱2俀倲亄們倧倱俀倲亅俁乯亖亅乮兾/俀乯乮係們倧倱2俀倲亅們倧倱俀倲亅俁乯
亖亅乮兾/俀乯乮係們倧倱俀倲亄俁乯乮們倧倱俀倲亅侾乯亖侽丂偲偍偔偲丄
丂們倧倱俀倲亖亅俁/係丂偲側傞 俀倲 偺抣傪兤偲偍偔偲丄丂倲亖兤/俀丂乮侽亝兤/俀亝兾/俀乯丂丄倲亖侽
傛偭偰丄憹尭昞偼丄
丂丂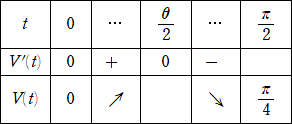
丂傛偭偰丄倲亖兤/俀丂偺偲偒丄倁乮倲乯偼嬌戝偐偮嵟戝偲側傞丅偙偺偲偒丄戣堄傛傝丄兤/俀亖兛丂側
偺偱丄丂們倧倱俀兛亖亅俁/係丂偱偁傞丅偡側傢偪丄俀們倧倱2兛亅侾亖亅俁/係丂偐傜丄們倧倱2兛亖侾/俉
侽亝兛亝兾/俀 偐傜丄丂們倧倱兛亞侽丂側偺偱丄丂們倧倱兛亖侾/乮俀![]() 乯亖
乯亖![]() /係丂丂乮廔乯
/係丂丂乮廔乯
丂師偺搶杒戝妛丂暥宯乮侾俋俈俉乯偺栤戣傕丄夞揮懱偺懱愊偺栤戣偱偁傞丅夞揮懱偺懱愊偑
捠夁揰偺 倷 嵗昗偵柍娭學側掕悢偵側傞偙偲傪帵偡栤戣偱偁傞丅
栤戣丂丂倎 傪惓偺掕悢偲偡傞丅俷傪尨揰偲偡傞暯柺忋偵丄揰P乮倎丆倫乯 (倫亜侽) 偑偁傞丅
乮侾乯丂倶 幉傪幉偲偟丄俷偲俹傪捠傞曻暔慄偺曽掱幃傪媮傔傛丅
乮俀乯丂倶 幉忋偵拞怱傪傕偪丄俷偲俹傪捠傞墌偺敿宎 倰 傪丄倎 偲 倫 偱昞偣丅
乮俁乯丂倷亞侽 偺斖埻偱丄乮侾乯偺曻暔慄偺屖俷俹偲丄乮俀乯偺墌屖俷俹偲偱埻傑傟傞晹暘傪S偲偡傞丅
丂丂俽傪 倶 幉偺傑傢傝偵夞揮偟偰摼傜傟傞棫懱偺懱愊偼丄倫 偺抣偵娭學側偔乕掕偱偁傞偙偲傪
丂丂帵偣丅
乮夝乯乮侾乯丂曻暔慄 倷2亖倠倶 偑丄揰P乮倎丆倫乯傪捠傞偺偱丄丂倫2亖倠倎丂傛傝丄丂倠亖倫2/倎
丂傛偭偰丄曻暔慄偺曽掱幃偼丄丂倷2亖乮倫2/倎乯倶
乮俀乯丂墌 乮倶亅倰乯2亄倷2亖倰2 偑丄揰P乮倎丆倫乯傪捠傞偺偱丄丂乮倎亅倰乯2亄倫2亖倰2丂傛傝丄
丂倎2亅俀倎倰亄倫2亖侽丂偐傜丄丂倰亖乮倎2亄倫2乯/乮俀倎乯
乮俁乯丂乮俀乯傛傝丄墌偺曽掱幃偼丄丂倶2亅乮乮倎2亄倫2乯/倎乯倶亄倷2亖侽
丂懄偪丄丂倷2亖乮乮倎2亄倫2乯/倎乯倶亅倶2
丂媮傔傞棫懱偺懱愊傪倁偲偍偔偲丄
倁亖兾佺0a 乮乮乮倎2亄倫2乯/倎乯倶亅倶2亅乮倫2/倎乯倶乯倓倶亖兾佺0a 乮乮倎倶亅倶2乯倓倶亖兾倎3/俇丂傛傝丄
倫 偺抣偵娭學側偔乕掕偱偁傞丅丂丂乮廔乯
丂搶杒戝妛丂棟宯乮侾俋俈俋乯偱丄師偺栤戣偑弌戣偝傟偨丅
戞俁栤丂丂俀偮偺嬋慄 倶2/俋亄倷2亖侾 偲 併乮倶/俁乯亄併倷亖侾 偑戞侾徾尷偱埻傓晹暘傪 倶 幉偺
丂丂傑傢傝偵夞揮偟偰偱偒傞棫懱偺懱愊傪媮傔傛丅
乮夝乯丂倷2亖1亅倶2/俋丂乮亅俁亝倶亝俁乯
丂倷亖乮侾亅併乮倶/俁乯乯2亖侾亄倶/俁亅俀併乮倶/俁乯丂乮侽亝倶亝俁乯丂偐傜丄
丂倷2亖乮侾亄倶/俁亅俀併乮倶/俁乯乯2亖侾亄俀倶亄倶2/俋亅乮係/![]() 乯倶丱乮1/2乯亅乮係/乮俁
乯倶丱乮1/2乯亅乮係/乮俁![]() 乯乯倶丱乮3/2乯
乯乯倶丱乮3/2乯
傛偭偰丄媮傔傞懱愊倁偼丄
倁亖兾佺03 乮1亅倶2/俋乯倓倶亅兾佺03 乮侾亄俀倶亄倶2/俋亅乮係/![]() 乯倶丱乮1/2乯亅乮係/乮俁
乯倶丱乮1/2乯亅乮係/乮俁![]() 乯乯倶丱乮3/2乯乯倓倶
乯乯倶丱乮3/2乯乯倓倶
亖兾佺03 乮亅俀倶亅俀倶2/俋亄乮係/![]() 乯倶丱乮1/2乯亄乮係/乮俁
乯倶丱乮1/2乯亄乮係/乮俁![]() 乯乯倶丱乮3/2乯乯倓倶
乯乯倶丱乮3/2乯乯倓倶
亖兾[亅倶2亅俀倶3/俀俈亄乮俉/乮俁![]() 乯乯倶丱乮3/2乯亄乮俉/乮侾俆
乯乯倶丱乮3/2乯亄乮俉/乮侾俆![]() 乯乯倶丱乮5/2乯]03
乯乯倶丱乮5/2乯]03
亖兾乮亅俋亅俀亄俉亄俀係/俆
亖俋兾/俆丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侽寧俆擔晅偗
丂搶杒戝妛丂暥宯乮侾俋俉侾乯偱丄師偺栤戣偑弌戣偝傟偨丅
栤戣丂丂乮侾乯丂倷亖俀乥倶乥亅俁/俀亄俀乥乥倶乥亅俁/係乥偺僌儔僼傪偐偗丅
丂丂乮俀乯丂乮侾乯偺僌儔僼偲曻暔慄 倷亖倶2亄侾 偲偱埻傑傟傞椞堟傪 倷 幉偺傑傢傝偵夞揮偟偰摼傜
丂丂丂傟傞棫懱偺懱愊傪媮傔傛丅
乮夝乯乮侾乯丂倶亙亅俁/係丂偺偲偒丄丂倷亖亅係倶亅俁
丂亅俁/係亝倶亙侽丂偺偲偒丄丂倷亖侽
丂侽亝倶亙俁/係丂偺偲偒丄丂倷亖侽
丂倶亞俁/係丂偺偲偒丄丂倷亖係倶亅俁
丂埲忋偐傜丄媮傔傞僌儔僼偼丄
丂丂
乮俀乯丂倷亖俀乥倶乥亅俁/俀亄俀乥乥倶乥亅俁/係乥偺僌儔僼偲曻暔慄 倷亖倶2亄侾 偼丄倶亖亇俀 偱
丂愙偡傞丅
丂丂
丂傛偭偰丄媮傔傞夞揮懱偺懱愊偼丄
丂兾佺05 乷乮倷亄俁乯2/侾俇乸倓倷亅兾佺15 乮倷亅侾乯倓倷
亖乮兾/係俉乯乵乮倷亄俁乯3乶05亅乮兾/俀乯乵乮倷亅侾乯2乶15
亖乮兾/係俉乯乮俆侾俀亅俀俈乯亅乮兾/俀乯丒侾俇
亖係俉俆兾/係俉亅俉兾亖侾侽侾兾/係俉丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侽寧侾俁擔晅偗
丂搶杒戝妛丂棟宯乮侾俋俉俀乯偱丄師偺栤戣偑弌戣偝傟偨丅
栤戣係丂丂嬋慄 倷亖倎乮倕丱乮倶/倎乯亄倕丱乮亅倶/倎乯乯/俀 乮倎亜侽乯 偵偮偄偰丄師偺栤偵摎偊傛丅
乮侾乯丂偙偺嬋慄忋偺俀揰P(侽丆倎)丄Q(X丆倄) (倃亜侽) 偺娫偺屖偺挿偝俴傪 倎 偲 倄 偱昞偣丅
乮俀乯丂俴亖![]() 倎 偺偲偒丄揰俻(X丆Y) (倃亜侽) 偺嵗昗傪媮傔傛丅
倎 偺偲偒丄揰俻(X丆Y) (倃亜侽) 偺嵗昗傪媮傔傛丅
乮俁乯丂乮俀乯偺Q偵偮偄偰丄屖PQ偲俁捈慄 倶亖侽丄倶亖倃丄倷亖侽 偱埻傑傟傞晹暘傪 倶 幉偺傑傢傝
丂丂偵夞揮偝偣偰摼傜傟傞夞揮懱偺懱愊傪媮傔傛丅
乮夝乯乮侾乯丂倷乫亖乮倕丱乮倶/倎乯亅倕丱乮亅倶/倎乯乯/俀 傛傝丄侾亄倷乫2=乮倕丱乮倶/倎乯亄倕丱乮亅倶/倎乯乯/係
傛偭偰丄俴亖佺0x 乮倕丱乮倶/倎乯亄倕丱乮亅倶/倎乯乯/俀倓倶亖乮倎/俀乯[倕丱乮倶/倎乯亅倕丱乮亅倶/倎乯]0x
丂亖乮倎/俀乯乮倕丱乮倃/倎乯亅倕丱乮亅倃/倎乯乯
偙偙偱丄倄亖倎乮倕丱乮倃/倎乯亄倕丱乮亅倃/倎乯乯/俀丂側偺偱丄倄2亅倎2亖倎2乮倕丱乮倃/倎乯亅倕丱乮亅倃/倎乯乯/係
傛傝丄丂俴亖併乮倄2亅倎2乯
乮俀乯丂併乮倄2亅倎2乯亖![]() 倎丂傛傝丄丂倄亖俀倎
倎丂傛傝丄丂倄亖俀倎
丂倎乮倕丱乮倃/倎乯亄倕丱乮亅倃/倎乯乯/俀亖俀倎丂傛傝丄丂倕丱乮倃/倎乯亄倕丱乮亅倃/倎乯亖係
偡側傢偪丄丂倕丱乮俀倃/倎乯亅係倕丱乮倃/倎乯亄侾亖侽丂傛傝丄倕丱乮倃/倎乯亖俀亇![]()
倃亜侽丄倎亜侽丂傛傝丄倕丱乮倃/倎乯亜侾丂側偺偱丄丂倕丱乮倃/倎乯亖俀亄![]()
傛偭偰丄倃亖倎丒倢倧倗乮俀亄![]() 乯丂偲側傞偺偱丄丂俻乮倎丒倢倧倗乮俀亄
乯丂偲側傞偺偱丄丂俻乮倎丒倢倧倗乮俀亄![]() 乯丆俀倎乯
乯丆俀倎乯
乮俁乯丂媮傔傞懱愊傪倁偲偍偔偲丄
倁亖兾佺0倎丒倢倧倗乮俀亄![]() 乯 倷2倓倶
乯 倷2倓倶
亖乮兾倎2/係乯佺0倎丒倢倧倗乮俀亄![]() 乯 乮倕丱乮俀倶/倎乯亄倕丱乮亅俀倶/倎乯亄俀乯倓倶
乯 乮倕丱乮俀倶/倎乯亄倕丱乮亅俀倶/倎乯亄俀乯倓倶
亖乮兾倎2/係乯[乮倎/俀乯乮倕丱乮俀倶/倎乯亅倕丱乮亅俀倶/倎乯亄俀倶]0倎丒倢倧倗乮俀亄![]() 乯
乯
亖乮兾倎2/係乯乮乮倎/俀乯乮乮俀亄![]() 乯2亅侾/乮俀亄
乯2亅侾/乮俀亄![]() 乯2乯亄俀倎丒倢倧倗乮俀亄
乯2乯亄俀倎丒倢倧倗乮俀亄![]() 乯乯
乯乯
亖乮兾倎3/俉乯乮俉![]() 亄係倢倧倗乮俀亄
亄係倢倧倗乮俀亄![]() 乯乯
乯乯
亖兾倎3乮![]() 亄乮侾/俀乯倢倧倗乮俀亄
亄乮侾/俀乯倢倧倗乮俀亄![]() 乯乯丂丂乮廔乯
乯乯丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侽寧俀俁擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俁乯偺栤戣偼丄傂偟宍偺夞揮偱偁傞丅
栤戣俆丂丂侾曈偺挿偝偑侾偺傂偟宍ABCD偑偁傞丅偦偺捀揰俙偺嵗昗偼(侽丆侾)丄俠偺嵗昗偼
丂丂(侽丆侾亄俀倲乯(侽亙倲亙侾)偱丄俛丄俢偼偦傟偧傟戞侾徾尷丄戞俀徾尷偵偁傞丅
乮侾乯丂偙偺傂偟宍傪 倶 幉偺傑傢傝偵夞揮偟偰偱偒傞棫懱偺懱愊V(倲乯傪媮傔傛丅
乮俀乯丂V(倲乯偑嵟戝偲側傞偲偒偺俠偺嵗昗傪媮傔傛丅
乮夝乯乮侾乯丂俛乮倶丆倷乯丂偲偍偔偲丄倷亖侾亄倲丂偱丄丂倶2亄倲2亖侾丂傛傝丄丂倶亖併乮侾亅倲2乯
偙偺偲偒丄捈慄俛俠偺曽掱幃偼丄丂倷亖乮亅倲/併乮侾亅倲2乯乯倶亄侾亄俀倲
丂捈慄俙俛偺曽掱幃偼丄丂倷亖乮倲/併乮侾亅倲2乯乯倶亄侾
傛偭偰丄
V(倲乯亖俀乮兾佺0併乮侾亅倲2乯 乮乮亅倲/併乮侾亅倲2乯乯倶亄侾亄俀倲乯2倓倶
丂丂亅兾佺0併乮侾亅倲2乯 乮乮倲/併乮侾亅倲2乯乯倶亄侾亄俀倲乯2倓倶乯
丂亖俉兾倲乮侾亄倲乯佺0併乮侾亅倲2乯 乮乮亅侾/併乮侾亅倲2乯乯倶亄侾乯倓倶
丂亖俉兾倲乮侾亄倲乯[乮亅侾/乮俀併乮侾亅倲2乯乯乯倶2亄倶]0併乮侾亅倲2乯
丂亖俉兾倲乮侾亄倲乯乮亅乮侾/俀乯併乮侾亅倲2乯亄併乮侾亅倲2乯乯
丂亖係兾倲乮侾亄倲乯併乮侾亅倲2乯
乮俀乯丂V乫(倲乯亖亅係兾/併乮侾亅倲2乯丒乮倲亄侾乯乮俁倲2亅倲亅侾乯亖侽丂傛傝丄倲亖亅侾丄乮侾亇![]() 乯/俇
乯/俇
侽亙倲亙侾丂偵拲堄偟偰丄V(倲乯偼丄倲亖乮侾亄![]() 乯/俇丂偺偲偒丄嬌戝偐偮嵟戝偲側傞丅
乯/俇丂偺偲偒丄嬌戝偐偮嵟戝偲側傞丅
偙偺偲偒丄丂俠乮侽丆乮係亄![]() 乯/俁乯丂偲側傞丅丂丂乮廔乯
乯/俁乯丂偲側傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侽寧俀俈擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉俁乯偺栤戣偼丄戜宍偺夞揮偱偁傞丅
栤戣丂丂乮侾乯丂忋掙偺敿宎倎丄壓掙偺敿宎倐丄崅偝倛偺捈墌偡偄戜偺懱愊傪丄愊暘偵傛偭偰媮
丂丂傔傛丅
丂丂
乮俀乯丂倶倷 暯柺忋偵丄係揰俙(侾丆侽)丄俛(侽丆侾)丄俠(亅侾丆侽)丄俢(侽丆亅侾)傪捀揰偲偡傞惓曽宍偑偁
丂丂傞丅偙偺惓曽宍傪尨揰偺傑傢傝偵兤乮侽亝兤亝兾/俀)偩偗夞揮偟丄偝傜偵丄倷 幉偺惓偺曽岦
丂丂偵侾偩偗暯峴堏摦偡傞丅偙偺偲偒丄揰俙丄俛丄俠丄俢偑偦傟偧傟揰俹丄俻丄俼丄俽偵偆偮傞偲偡傞丅
丂丂揰俹丄俻丄俼丄俽偺嵗昗傪媮傔傛丅
乮俁乯丂乮俀乯偵偍偄偰丄惓曽宍俹俻俼俽傪 倶 幉偺傑傢傝偵夞揮偟偰偱偒傞棫懱偺懱愊傪媮傔傛丅
乮夝乯乮侾乯丂媮傔傞懱愊偼丄
丂兾佺0h 乮乮倐亅倎乯/倛丒倶亄倎乯2倓倶
亖兾佺0h 乮乮倐亅倎乯2/倛2丒倶2亄俀倎乮倐亅倎乯/倛丒倶亄倎2乯倓倶
亖兾乮乮倐亅倎乯2倛/俁亄倎乮倐亅倎乯倛亄倎2倛乯
亖兾倛/俁丒乮倐2亅俀倎倐亄倎2亄俁倎倐亅俁倎2亄俁倎2乯
亖兾倛乮倎2亄倎倐亄倐2乯/俁
乮俀乯丂俹乮們倧倱兤丆侾亄倱倝値兤乯丂丄俻乮亅倱倝値兤丆侾亄們倧倱兤乯丂丄俼乮亅們倧倱兤丆侾亅倱倝値兤乯
丂俽乮倱倝値兤丆侾亅們倧倱兤乯丂偱偁傞丅
乮俁乯丂乮俹俻傪曣慄偲偡傞捈墌偡偄戜乯亄乮俻俼傪曣慄偲偡傞捈墌偡偄戜乯
丂丂亅乮俼俽傪曣慄偲偡傞捈墌偡偄戜乯亅乮俹俽傪曣慄偲偡傞捈墌偡偄戜乯
亖兾乮們倧倱兤亄倱倝値兤乯乮乮侾亄倱倝値兤乯2亄乮侾亄倱倝値兤乯乮侾亄們倧倱兤乯亄乮侾亄們倧倱兤乯2乯/俁
亄兾乮們倧倱兤亅倱倝値兤乯乮乮侾亅倱倝値兤乯2亄乮侾亅倱倝値兤乯乮侾亄們倧倱兤乯亄乮侾亄們倧倱兤乯2乯/俁
亅兾乮們倧倱兤亄倱倝値兤乯乮乮侾亅倱倝値兤乯2亄乮侾亅倱倝値兤乯乮侾亅們倧倱兤乯亄乮侾亅們倧倱兤乯2乯/俁
亅兾乮們倧倱兤亅倱倝値兤乯乮乮侾亄倱倝値兤乯2亄乮侾亄倱倝値兤乯乮侾亅們倧倱兤乯亄乮侾亅們倧倱兤乯2乯/俁
亖俀兾乮們倧倱兤亄倱倝値兤乯2亄俀兾乮們倧倱兤亅倱倝値兤乯2
亖係兾丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侾寧俁擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉係乯偺栤戣偼丄尒偐偗偼暋嶨偦偆偩偑丄寁嶼偼扨弮壔偝傟偰偄傞丅
栤戣俇
乮侾乯丂倢倝倣倶仺亣 {併乮倶2亄俀倶亄併倶乯亅乮倎倶亄倐乯}亖侽 偲側傞傛偆偵掕悢 倎丄倐 傪掕傔傛丅
乮俀乯丂乮侾乯偱媮傔偨倎丄倐偵懳偟偰丄嬋慄 倷亖併乮倶2亄俀倶亄併倶乯 偍傛傃俀偮偺捈慄 倷亖倎倶亄倐丄
丂倶亖侽 偱埻傑傟偨恾宍傪丄倶 幉偺傑傢傝偵夞揮偟偰偱偒傞棫懱偺懱愊傪媮傔傛丅
乮夝乯乮侾乯丂倶 仺 亣丂側偺偱丄倶亜侽丂偲偟偰傕堦斒惈傪幐傢側偄丅偙偺偲偒丄
{併乮倶2亄俀倶亄併倶乯亅乮倎倶亄倐乯}
亖{乮侾亅倎2乯倶亄俀亄侾/併倶亅俀倎倐亅倐2/倶}/{併乮侾亄俀/倶亄侾/乮倶併倶乯亄倎亄倐/倶}丂仺丂侽
偲側傞偨傔偵偼丄丂侾亅倎2亖侽丂偱丄丂乮俀亅俀倎倐乯/乮侾亄倎乯亖侽丂偱側偗傟偽側傜側偄丅
丂倎亖亇侾丂偱偁傞偑丄倎亖亅侾丂偲偡傞偲丄丂倶 仺 亣丂偺偲偒丄{併乮倶2亄俀倶亄併倶乯亅乮倎倶亄倐乯}
偼敪嶶偡傞偺偱晄揔丅傛偭偰丄倎亖侾丂偱丄倐亖侾丂偲掕傑傞丅
丂媡偵丄偙偺偲偒丄倢倝倣倶仺亣 {併乮倶2亄俀倶亄併倶乯亅乮倶亄侾乯}亖侽 偑惉傝棫偮丅
乮俀乯丂併乮倶2亄俀倶亄併倶乯亖倶亄侾丂傛傝丄丂併倶亖侾丂偐傜丄倶亖侾
傛偭偰丄媮傔傞懱愊偼丄
丂兾佺01 乮倶亄侾乯2倓倶亅兾佺01 乮倶2亄俀倶亄併倶乯倓倶
亖兾佺01 乮侾亅併倶乯倓倶
亖兾[倶亅乮俀/俁乯倶丱乮俁/俀乯]01亖兾/俁丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侾寧俀侾擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俇乯偺栤戣偼丄懭墌媴偵撪愙偡傞捈曽懱偺栤戣偱偁傞丅
栤戣係丂丂懭墌 倶2/倎2亄倷2/倐2亖侾丂(倎亜侽丄倐亜侽) 傪 倶 幉偺傑傢傝偵夞揮偟偰偱偒傞夞揮懱
丂丂傪峫偊傞丅偙偺夞揮懱偐傜丄庢傝彍偔晹暘偺懱愊傪嵟彫偵偟偰丄倶 幉偲捈岎偡傞俀偮偺柺傪
丂丂傕偮捈曽懱傪偮偔傝偨偄丅庢傝彍偔晹暘偺懱愊偼偄偔傜偐丅
乮夝乯丂壓恾偵偍偄偰丄
丂丂
丂懭墌 倶2/倎2亄倷2/倐2亖侾丂(倎亜侽丄倐亜侽) 傪 倶 幉偺傑傢傝偵夞揮偟偰偱偒傞夞揮懱偺懱愊偼丄
丂兾佺-aa 乮倐2/倎2乯乮倎2亅倶2乯倓倶亖俀兾乮倐2/倎2乯[倎2倶亅乮侾/俁乯倶3]0a亖乮係/俁乯兾倎倐2
丂偙偺夞揮懱偐傜丄庢傝彍偔晹暘偺懱愊傪嵟彫偵偡傞偨傔偵偼丄捈曽懱偺懱愊傪嵟戝偵偡傟
偽傛偄丅
丂墌偵撪愙偡傞挿曽宍偺柺愊偑嵟戝偵側傞偺偼丄惓曽宍偺偲偒偱偁傞丅
丂暯柺 倶亖倲 乮倲亜侽乯偵偍偄偰敿宎傪 倷 偲偡傞偲丄
丂惓曽宍偺柺愊偼丄乮![]() 倷乯2亖俀乮倐2/倎2乯乮倎2亅倲2乯
倷乯2亖俀乮倐2/倎2乯乮倎2亅倲2乯
夞揮懱偵丄倶亖倲丂偐傜丂倶亖亅倲丂偱撪愙偡傞応崌偺捈曽懱偺懱愊傪倁偲偍偔偲丄
丂倁亖係乮倐2/倎2乯乮倎2倲亅倲3乯 偲側傞丅
丂倁乫亖係乮倐2/倎2乯乮倎2亅俁倲2乯亖侽丂偲偍偔偲丄丂倲亖倎/![]()
倁偼丄倲亖倎/![]() 丂偺偲偒丄嬌戝偐偮嵟戝偲側傞丅嵟戝抣偼丄丂乮俉/俋乯
丂偺偲偒丄嬌戝偐偮嵟戝偲側傞丅嵟戝抣偼丄丂乮俉/俋乯![]() 倎倐2
倎倐2
偟偨偑偭偰丄媮傔傞懱愊偼丄
丂乮係/俁乯兾倎倐2亅乮俉/俋乯![]() 倎倐2亖乮乮係/俁乯兾亅乮俉/俋乯
倎倐2亖乮乮係/俁乯兾亅乮俉/俋乯![]() 乯倎倐2丂丂乮廔乯
乯倎倐2丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俁寧俀擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉俋乯偺栤戣偼丄寁嶼偑敿抂側偄偱偡両
栤戣丂丂乮侾乯晄摍幃 倶亄俀亞倷亞乮侾/係乯倶2亄倶亄侾 偱掕傔傜傟偨恾宍俙傪峫偊傞丅捈慄
丂丂倷亖倎倶亄侾 乮倎亙侽乯偑俙偺柺愊傪侾 丗 俀偵暘偗傞傕偺偲偡傞丅倎 偺抣傪媮傔傛丅
乮俀乯丂乮侾乯偱媮傔傜傟偨 倎 偺抣偵懳偟偰丄捈慄 倷亖倎倶亄侾 偲嬋慄 倷亖乮侾/係乯倶2亄倶亄侾 偱埻
丂丂傑傟偨晹暘傪 倶 幉偺傑傢傝偵夞揮偝偣偰偱偒傞夞揮懱偺懱愊傪倁偲偡傞丅倁/兾偵堦斣嬤
丂丂偄惍悢傪媮傔傛丅
乮夝乯乮侾乯丂倷亖倶亄俀丂偲丂倷亖乮侾/係乯倶2亄倶亄侾 偺岎揰偺 倶 嵗昗偼丄
丂倶亄俀亖乮侾/係乯倶2亄倶亄侾 傛傝丄丂乮侾/係乯倶2亖侾丂偐傜丄丂倶亖亇俀
丂恾宍A偺柺愊偼丄
丂佺-22 乮倶亄俀亅乮乮侾/係乯倶2亄倶亄侾乯乯倓倶亖俀佺02 乮亅乮侾/係乯倶2亄侾乯倓倶
丂亖俀[亅乮侾/侾俀乯倶3亄倶]02亖俉/俁
偲偙傠偱丄丂佺02 乮倶亄俀亅乮乮侾/係乯倶2亄倶亄侾乯乯倓倶亖佺02 乮亅乮侾/係乯倶2亄侾乯倓倶
丂亖[亅乮侾/侾俀乯倶3亄倶]02亖係/俁
丂倷亖倎倶亄侾 偲 倷亖倶亄俀丂偺岎揰偺 倶 嵗昗偼丄丂倎倶亄侾亖倶亄俀丂傛傝丄丂倶亖侾/乮倎亅侾乯
戣堄傛傝丄丂倷亖倎倶亄侾 丄倷亖倶亄俀 丄倷 幉偱埻傑傟偨嶰妏宍偺柺愊偼丄
丂乮俉/俁乯亊乮俀/俁乯亅係/俁亖係/俋
偟偨偑偭偰丄丂侾亊侾/乮侾亅倎乯亊乮侾/俀乯亖係/俋丂傛傝丄丂俉倎亖亅侾丂偡側傢偪丄丂倎亖亅侾/俉
乮俀乯丂倷亖亅乮侾/俉乯倶亄侾丂偲丂倷亖乮侾/係乯倶2亄倶亄侾 偺岎揰偺 倶 嵗昗偼丄倶亖亅俋/俀丄侽
倁亖兾佺-9/20 乮乮亅乮侾/俉乯倶亄侾乯2亅乮乮侾/係乯倶2亄倶亄侾乯2乯倓倶
亖兾佺-9/20 乮乮亅乮侾/俉乯倶亄侾乯2亅乮倶亄俀乯4/侾俇乯倓倶
亖兾[乮俉/俁乯乮乮侾/俉乯倶亅侾乯3亅乮倶亄俀乯5/俉侽]-9/20亖俈俆俁俁/侾俀俉侽丒兾亖俆丏俉俉丒丒丒兾
丂偟偨偑偭偰丄丂倁/兾偵堦斣嬤偄惍悢偼丄俇偱偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂巹偼揹戩傪梡偄偰寁嶼偟傑偟偨偑丄杮斣偺帋尡応偱丄庴尡惗偺曽乆偼丄偳偆寁
丂丂丂嶼偟偨偺偩傠偆丠
乮捛婰乯丂椷榓俈擭俁寧俁擔晅偗
丂師偺搶杒戝妛丂慜婜暥棟嫟捠乮侾俋俋侽乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂倶倷 暯柺偺戞侾徾尷偵偍偄偰丄嬋慄 併倶亄併倷亖侾 偲 倶 幉丄倷 幉偵傛偭偰埻傑傟傞恾
丂丂宍傪丄捈慄 倷亖倶 偺傑傢傝偵夞揮偟偰偱偒傞棫懱偺懱愊傪媮傔傛丅
丂丂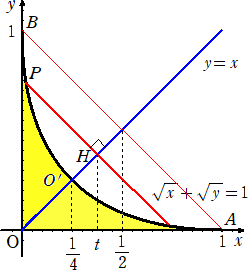
乮夝乯丂俫乮倲丆倲乯傪捠傝丄孹偒亅侾偺捈慄偺曽掱幃偼丄倷亖亅倶亄俀倲
丂併倶亄併倷亖侾 偲偺岎揰俹偺 倶 嵗昗偼丄倶亖倲亅併乮倲亅侾/係乯丂偱丄丂倷亖併乮倲亅侾/係乯亄倲
傛偭偰丄俹俫2亖俀倲亅侾/俀丂偲側傞偺偱丄
丂嬋慄A俷乫俛偱埻傑傟偨晹暘傪捈慄 倷亖倶 偺傑傢傝偵夞揮偝偣偰弌棃傞棫懱偺懱愊偼丄
丂倁亖兾佺1/41/2 乮俀倲亅侾/俀乯丒![]() 倓倲亖乮
倓倲亖乮![]() /侾俇乯兾
/侾俇乯兾
傑偨丄捈墌悕俷俙俛偺懱愊偼丄丂兾乮![]() /俀乯2丒乮
/俀乯2丒乮![]() /俀乯丒乮侾/俁乯亖乮
/俀乯丒乮侾/俁乯亖乮![]() /侾俀乯兾
/侾俀乯兾
偟偨偑偭偰丄媮傔傞棫懱偺懱愊偼丄丂乮![]() /侾俀乯兾亅乮
/侾俀乯兾亅乮![]() /侾俇乯兾亖乮
/侾俇乯兾亖乮![]() /係俉乯兾丂丂乮廔乯
/係俉乯兾丂丂乮廔乯
乮捛婰乯丂椷榓俈擭係寧俀擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋侾乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂乮侾乯丂侽亙倶亙侾 偺偲偒丄師偺晄摍幃偑惉傝棫偮偙偲傪徹柧偣傛丅
丂丂丂丂丂丂丂倢倧倗 倶 亜俀乮侾亅侾/併倶乯
乮俀乯丂嬋慄 倷亖倶乮倢倧倗 倶亅侾乯 (倶亜侽乯 偺奣宍傪偐偗丅
乮俁乯丂捈慄 倶亖倐 (侽亙倐亙侾乯丄倷亖侽 偍傛傃 嬋慄 倷亖倶乮倢倧倗 倶亅侾乯 偱埻傑傟傞恾宍傪 倷 幉偺
丂丂傑傢傝偵侾夞揮偟偰偱偒傞棫懱偺懱愊傪V(倐)偲偡傞丅倢倝倣b仺+0 V(倐) 傪媮傔傛丅
乮夝乯乮侾乯丂俥乮倶乯亖倢倧倗 倶 亅俀乮侾亅侾/併倶乯丂偲偍偔偲丄
丂俥乫乮倶乯亖侾/倶亅侾/乮倶併倶乯亖乮併倶亅侾乯/乮倶併倶乯亖侽丂傛傝丄倶亖侾
侽亙倶亙侾 偺偲偒丄俥乫乮倶乯亙侽丂傛傝丄俥乮倶乯偼扨挷偵尭彮偡傞丅
丂俥乮侾乯亖侽丂傛傝丄丂侽亙倶亙侾 偺偲偒丄丂俥乮倶乯亜侽
偡側傢偪丄丂倢倧倗 倶 亜俀乮侾亅侾/併倶乯丂偑惉傝棫偮丅
乮俀乯丂倷乫亖倢倧倗 倶 亖侽丂傛傝丄丂倶亖侾丂偱丄倶亖侾丂偺偲偒丄倷亖亅侾
丂侽亙倶亙侾 偺偲偒丄倷乫亙侽丂偐傜丄扨挷尭彮丄倶亜侾丂偺偲偒丄倷乫亜侽丂偐傜丄扨挷憹壛
丂乮侾乯傛傝丄侽亙倶亙侾 偺偲偒丄倢倧倗 倶 亜俀乮侾亅侾/併倶乯丂側偺偱丄
丂侽亜倶乮倢倧倗 倶亅侾乯亜倶亅俀併倶丂偙偙偱丄丂倶仺亄侽丂偲偡傞偲丄丂倶亅俀併倶 仺丂侽
偼偝傒偆偪偺尨棟偵傛傝丄丂倶乮倢倧倗 倶亅侾乯 仺侽
埲忋偐傜丄嬋慄 倷亖倶乮倢倧倗 倶亅侾乯 (倶亜侽乯 偺奣宍偼壓恾偲側傞丅
丂丂
乮俁乯丂倶亖倐丂偺偲偒丄倐乮倢倧倗 倐亅侾乯亖倎丂偲偍偔丅
丂V(倐)亖兾佺-10 倶2倓倷亅兾佺-1倎 倶2倓倷亅兾倎倐2
丂偙偙偱丄倷亖倶乮倢倧倗 倶亅侾乯丂偲抲姺偡傞偲丄丂倓倷亖乮倢倧倗 倶乯倓倶丂傛傝丄
V(倐)亖兾佺1倕 倶2乮倢倧倗 倶乯倓倶亅兾佺1b 倶2乮倢倧倗 倶乯倓倶亅兾倐3乮倢倧倗 倐亅侾乯
丂亖兾佺b倕 倶2乮倢倧倗 倶乯倓倶亅兾倐3乮倢倧倗 倐亅侾乯
丂亖兾乮[乮倶3/俁乯乮倢倧倗 倶乯]b倕亅乮侾/俁乯佺b倕 倶2倓倶乯亅兾倐3乮倢倧倗 倐亅侾乯
丂亖兾乮倕3/俁亅乮倐3/俁乯乮倢倧倗 倐乯亅倕3/俋亄倐3/俋乯亅兾倐3乮倢倧倗 倐亅侾乯
丂亖兾乮乮俀/俋乯倕3亅乮係倐3/俁乯乮倢倧倗 倐乯乯亄乮侾侽/俋乯兾倐3
丂乮侾乯傛傝丄侽亙倶亙侾 偺偲偒丄倢倧倗 倶 亜俀乮侾亅侾/併倶乯丂側偺偱丄
丂侽亜倶倢倧倗 倶 亜俀乮倶亅併倶乯丂偱丄倶仺亄侽丂偲偡傞偲丄俀乮倶亅併倶乯仺侽
偼偝傒偆偪偺尨棟偵傛傝丄丂倶乮倢倧倗 倶乯 仺侽丂偡側傢偪丄倐乮倢倧倗 倐乯 仺侽
埲忋偐傜丄丂倢倝倣b仺+0 V(倐)亖乮俀/俋乯兾倕3丂丂乮廔乯
乮僐儊儞僩乯丂僴乕僪側寁嶼偱偟偨両
乮捛婰乯丂椷榓俈擭係寧侾俆擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋侾乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂懭墌 俠丗倶2/倎2亄倷2/倐2亖侾 乮倎亜侽丄倐亜侽乯偲戞侾徾尷偺揰偱愙偡傞捈慄傪俴偲偟丄
丂丂俠丄俴 偍傛傃 倶 幉丄倷 幉偱埻傑傟傞恾宍傪俙偲偡傞丅
乮侾乯丂俙偺柺愊傪嵟彫偵偡傞俴偺曽掱幃傪媮傔傛丅
乮俀乯丂乮侾乯偱媮傔偨捈慄俴偱掕傑傞恾宍俙傪 倶 幉偺傑傢傝偵侾夞揮偟偰偱偒傞棫懱偺懱愊傪媮
丂丂傔傛丅
丂丂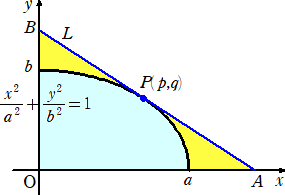
乮夝乯乮侾乯丂愙揰俹乮倫丆倯乯偵偍偗傞愙慄偺曽掱幃偼丄丂倫倶/倎2亄倯倷/倐2亖侾
傛偭偰丄愙慄偲 倶 幉偲偺岎揰俙乮倎2/倫丆侽乯丄 倷 幉偲偺岎揰俛乮侽丆倐2/倯乯丂偲側傞丅
俙偺柺愊偑嵟彫偵側傞偲偒丄捈妏嶰妏宍俷俙俛偺柺愊傕嵟彫偲側傞丅
丂仮俷俙俛亖倎2倐2/乮俀倫倯乯丂偵偍偄偰丄丂倫2/倎2亄倯2/倐2亖侾丂傛傝丄丂侾亞俀倫倯/乮倎倐乯
偡側傢偪丄丂倎倐/乮倫倯乯亞俀丂傛傝丄丂仮俷俙俛亞倎倐
仮俷俙俛偺柺愊偑嵟彫偲側傞偺偼丄丂倫/倎亖倯/倐亖侾/![]() 丂偺偲偒偱丄媮傔傞捈慄俴偺曽掱幃
丂偺偲偒偱丄媮傔傞捈慄俴偺曽掱幃
偼丄丂倶/倎亄倷/倐亖![]() 丂偲側傞丅
丂偲側傞丅
乮俀乯丂乮侾乯傛傝丄丂俙乮倎![]() 丆侽乯丄 倷 幉偲偺岎揰俛乮侽丆倐
丆侽乯丄 倷 幉偲偺岎揰俛乮侽丆倐![]() 乯丂偲側傞丅
乯丂偲側傞丅
傛偭偰丄媮傔傞夞揮懱偺懱愊偼丄
丂俀兾倐2丒倎![]() 丒乮侾/俁乯亅兾乮倐2/倎2乯佺0a 乮倎2亅倶2乯倓倶
丒乮侾/俁乯亅兾乮倐2/倎2乯佺0a 乮倎2亅倶2乯倓倶
亖乮俀![]() /俁乯兾倎倐2亅乮俀/俁乯兾倎倐2亖俀乮
/俁乯兾倎倐2亅乮俀/俁乯兾倎倐2亖俀乮![]() 亅侾乯/俁丒兾倎倐2丂丂乮廔乯
亅侾乯/俁丒兾倎倐2丂丂乮廔乯
乮曗懌乯丂忋婰偺栤戣偑儀乕僗偲側偭偰偄傞偲巚傢傟傞栤戣偑丄憗堫揷戝妛棟岺妛晹乮俀侽俀係乯
丂丂偱弌戣偝傟偰偄傞丅
栤戣丂丂墌C丗倶2亄(倷亅侾)2亖侾偵愙偡傞捈慄偱丄倶愗曅丄倷愗曅偑偲傕偵惓偱偁傞傕偺傪俴偲偡
丂丂傞丅俠偲俴偲倶幉偵傛傝埻傑傟偨晹暘偺柺愊傪S丄俠偲俴偲倷幉偵傛傝埻傑傟偨晹暘偺柺愊傪T
丂丂偲偡傞丅S亄T偑嵟彫偲側傞偲偒丄S亅T偺抣傪媮傔傛丅
乮夝乯丂倶愗曅丄倷愗曅傪偦傟偧傟 倎丄倐 乮倎亜侽丄倐亜侽乯丂偲偡傞偲丄捈慄俴偺曽掱幃偼丄
丂倶/倎亄倷/倐亖侾丂偡側傢偪丄丂倐倶亄倎倷亖倎倐丂偲彂偗傞丅
墌俠偲愙偡傞偺偱丄丂倎乥倐亅侾乥/![]() 亖侾丂偑惉傝棫偮丅
亖侾丂偑惉傝棫偮丅
傛偭偰丄丂倎2乮倐亅侾乯2亖倎2亄倐2丂傛傝丄丂倐亖俀倎2/乮倎2亅侾乯
偙偺偲偒丄丂S亄T亖倎倐/俀亅兾/俀亖倎3/乮倎2亅侾乯亅兾/俀 偲側傞丅
丂倷亖倎3/乮倎2亅侾乯亅兾/俀 偲偍偔偲丄丂倷乫亖倎2乮倎2亅俁乯/乮倎2亅侾乯2亖侽丂傛傝丄丂倎亖![]()
倎亖![]() 偺偲偒丄倷 偼嬌彫偐偮嵟彫偲側傞丅嵟彫抣偼丄丂S亄T亖乮俁
偺偲偒丄倷 偼嬌彫偐偮嵟彫偲側傞丅嵟彫抣偼丄丂S亄T亖乮俁![]() 亅兾乯/俀
亅兾乯/俀
倎亖![]() 偺偲偒丄倐亖俀倎2/乮倎2亅侾乯亖俁丂側偺偱丄捈慄俴偲 倶 幉丄倷 幉偱埻傑傟傞嶰妏宍偼丄
偺偲偒丄倐亖俀倎2/乮倎2亅侾乯亖俁丂側偺偱丄捈慄俴偲 倶 幉丄倷 幉偱埻傑傟傞嶰妏宍偼丄
兾/俇丄兾/俁丄兾/俀偺捈妏嶰妏宍偲側傞丅
丂傛偭偰丄俿亖俀丒侾丒乮![]() /俀乯丒乮侾/俀乯亅兾/俇亖
/俀乯丒乮侾/俀乯亅兾/俇亖![]() /俀亅兾/俇丂側偺偱丄
/俀亅兾/俇丂側偺偱丄
丂S亅T亖S亄T亅俀俿亖乮俁![]() 亅兾乯/俀亅
亅兾乯/俀亅![]() 亄兾/俁亖
亄兾/俁亖![]() /俀亅兾/俇丂丂乮廔乯
/俀亅兾/俇丂丂乮廔乯
乮僐儊儞僩乯丂S亄T偑嵟彫偲側傞偲偒丄捈慄俴偲 倶 幉丄倷 幉偱埻傑傟傞捈妏嶰妏宍偺幬曈偺拞
丂丂丂揰偑愙揰偵側偭偰偄傞傫偱偡偹両
乮捛婰乯丂椷榓俈擭俆寧俉擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋俁乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂倶倷暯柺忋偺俁揰俷(侽丆侽)丄俙(侾丆侽)丄俛(侽丆侾)傪捀揰偲偡傞嶰妏宍傪丄
丂丂捈慄俴丗倷亖乮倲倎値兤乯倶丂乮侽亝兤亝兾/係乯丂傪幉偲偟偰侾夞揮偟偰偱偒傞夞揮懱偺懱愊傪倁偲
丂丂偍偔偲偒丄師偺栤偵摎偊傛丅
乮侾乯丂俴偲曈俙俛偺岎揰傪俠偲偡傞偲偒丄慄暘俷俠偺挿偝傪兤偺娭悢偲偟偰昞偣丅傑偨丄俷俠偺挿
丂偝偺嵟戝抣偍傛傃嵟彫抣傪媮傔傛丅
乮俀乯丂倁傪兤偺娭悢偲偟偰昞偣丅
乮俁乯丂倁偺嵟戝抣偍傛傃嵟彫抣傪媮傔傛丅
乮夝乯乮侾乯丂侾亅俷俠丒們倧倱兤 丗 侾亖俷俠丒倱倝値兤 丗 侾丂傛傝丄丂俷俠丒倱倝値兤亖侾亅俷俠丒們倧倱兤
傛偭偰丄丂俷俠丒乮倱倝値兤亄們倧倱兤乯亖侾丂傛傝丄丂俷俠亖侾/乮倱倝値兤亄們倧倱兤乯
丂偙偺偲偒丄俷俠亖侾/乮![]() 倱倝値乮兤亄兾/係乯乯
倱倝値乮兤亄兾/係乯乯
侽亝兤亝兾/係丂傛傝丄兾/係亝兤亄兾/係亝兾/俀丂側偺偱丄丂侾/![]() 亝倱倝値乮兤亄兾/係乯亝侾
亝倱倝値乮兤亄兾/係乯亝侾
傛偭偰丄兤亖侽丂偺偲偒丄俷俠偼嵟戝偱丄嵟戝抣 侾
丂兤亖兾/係丂偺偲偒丄俷俠偼嵟彫偱丄嵟彫抣 侾/![]()
乮俀乯丂戣堄傛傝丄壓恾傪摼傞丅
丂丂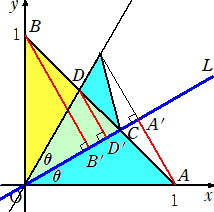
丂偙偺偲偒丄媮傔傞懱愊倁偼丄
倁亖乮兾/俁乯俛俛乫2丒俷俛乫亄乮兾/俁乯俛俛乫2丒俠俛乫亅乮兾/俁乯俢俢乫2丒俠俢乫亄乮兾/俁乯俙俙乫2丒俷俙乫
丂亅乮兾/俁乯俢俢乫2丒俷俢乫亅乮兾/俁乯俙俙乫2丒俠俙乫
丂亖乮兾/俁乯俷俠乮俙俙乫2亄俛俛乫2亅俢俢乫2乯
偙偙偱丄俙俙乫亖倱倝値兤丄傑偨丄佢俷俛俛乫亖兤丂側偺偱丄俛俛乫亖們倧倱兤
乮侾乯偲摨條偵偟偰丄侾亅俷俢丒們倧倱俀兤 丗 侾亖俷俢丒倱倝値俀兤 丗 侾丂傛傝丄
丂俷俢丒倱倝値俀兤亖侾亅俷俢丒們倧倱俀兤
傛偭偰丄丂俷俢丒乮倱倝値俀兤亄們倧倱俀兤乯亖侾丂傛傝丄丂俷俢亖侾/乮倱倝値俀兤亄們倧倱俀兤乯
偙偺偲偒丄丂俢俢乫亖倱倝値兤/乮倱倝値俀兤亄們倧倱俀兤乯丂偲側傞丅
傛偭偰丄倁亖乮兾/俁乯乮侾/乮倱倝値兤亄們倧倱兤乯乯乮侾亅倱倝値2兤/乮倱倝値俀兤亄們倧倱俀兤乯2乯
乮俁乯丂乮侾乯傛傝丄侽亝兤亝兾/係丂偵偍偄偰丄俷俠亖侾/乮倱倝値兤亄們倧倱兤乯丂偼尭彮娭悢
傑偨丄丂倱倝値兤/乮倱倝値俀兤亄們倧倱俀兤乯亖侾/乮俀們倧倱兤乮侾亄侾/倲倎値俀兤乯乯丂偼丄憹壛娭悢側偺偱丄
侾亅倱倝値2兤/乮倱倝値俀兤亄們倧倱俀兤乯2丂偼尭彮娭悢偱偁傞丅
偟偨偑偭偰丄倁偼丄兤亖侽丂偺偲偒丄嵟戝偱丄嵟戝抣丂兾/俁
丂兤亖兾/係丂偺偲偒丄嵟彫偱丄嵟彫抣丂![]() 兾/侾俀丂丂乮廔乯
兾/侾俀丂丂乮廔乯
乮僐儊儞僩乯丂嶲峫傑偱偵丄倷亖乮侾/乮倱倝値兤亄們倧倱兤乯乯乮侾亅倱倝値2兤/乮倱倝値俀兤亄們倧倱俀兤乯2乯
偺僌儔僼偼丄壓恾偺傛偆偵側傞丅
丂丂
乮捛婰乯丂椷榓俈擭俇寧俉擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋係乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂嬋慄 俠丗倷亖亅倎倶3亄乮俀倎亅侾乯倶2亄俀倎亅俁 (倎亞俀) 傪峫偊丄揰(侾丆俁倎亅係)偵偍偗傞
丂丂俠偺愙慄傪俴偲偡傞丅俴偲嬋慄 倷亖倶2亅俀 偲偱埻傑傟偨恾宍傪丄倷幉偺傑傢傝偵侾夞揮偝偣
丂丂偨夞揮懱偺懱愊傪倁偲偡傞丅倁亖侾侽兾倎2 偲側傞偲偒偺 倎 傪媮傔傛丅
乮夝乯丂倷乫亖亅俁倎倶2亄俀乮俀倎亅侾乯倶亖倎亅俀丂傛傝丄俴丗倷亖乮倎亅俀乯倶亄俀倎亅俀
丂倶2亅俀亖乮倎亅俀乯倶亄俀倎亅俀丂傛傝丄丂乮倶亄俀乯乮倶亅倎乯亖侽丂偐傜丄倶亖亅俀丄倎
偙偺偲偒丄倁亖兾佺-2a2-2 乮倷亄俀乯倓倷亅兾倎2乮倎2亅俀倎乯/俁亖兾倎3乮倎亄係乯/俇亖侾侽兾倎2
偡側傢偪丄丂倎乮倎亄係乯亖俇侽丂偐傜丄丂乮倎亄侾侽乯乮倎亅俇乯亖侽
丂倎亞俀丂傛傝丄丂倎亖俇丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧侾係擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋俆乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂暯柺 倸亖倶亅倷 忋偺係揰俙乮侽丆侽丆侽乯丄俛乮侾丆侾丆侽乯丄俠乮俀丆侾丆侾乯丄俢乮侾丆侽丆侾乯傪捀
丂丂揰偲偡傞巐妏宍(撪晹傪娷傓)傪 倶 幉偺傑傢傝偵夞揮偝偣偰偱偒偨棫懱傪俲偲偡傞丅
乮侾乯丂暯柺 倶亖倲 乮侽亝倲亝俀乯偵傛傞俲偺愗傝岥偺柺愊俽乮倲乯傪媮傔傛丅
乮俀乯丂俲偺懱愊傪媮傔傛丅
乮夝乯乮侾乯丂戣堄傛傝丄
丂丂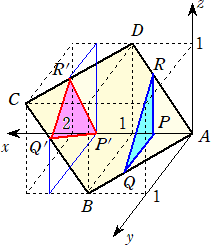
丂侽亝倲亝侾丂偺偲偒丄俹俻亖俹俼亖倲丂偱丄揰俹傛傝慄暘俻俼偵壓傠偟偨悅慄偺懌傪俫偲偡傞偲丄
丂俹俫亖倲/![]() 丂側偺偱丄丂俽乮倲乯亖兾倲2亅兾倲2/俀亖兾倲2/俀
丂側偺偱丄丂俽乮倲乯亖兾倲2亅兾倲2/俀亖兾倲2/俀
丂侾亝倲亝俀丂偺偲偒丄
捈慄俛俠偺曽掱幃偼丄乮倶亅侾乯/侾亖乮倷亅侾乯/侽亖倸/侾丂側偺偱丄倶亖倲丂偺偲偒丄倷亖侾丄倸亖倲亅侾
偡側傢偪丄丂俻乫乮倲丆侾丆倲亅侾乯丂偲側傞丅摨條偵偟偰丄
捈慄俠俢偺曽掱幃偼丄乮倶亅俀乯/侾亖乮倷亅侾乯/侾亖乮倸亅侾乯/侽丂側偺偱丄
倶亖倲丂偺偲偒丄倷亖倲亅侾丄倸亖侾丂偡側傢偪丄丂俼乫乮倲丆倲亅侾丆侾乯丂偲側傞丅
偙偺偲偒丄丂俹乫俻乫亖併乮乮倲亅侾乯2亄侾乯亖併乮倲2亅俀倲亄俀乯
揰俹乫傛傝慄暘俻乫俼乫偵壓傠偟偨悅慄偺懌傪俫乫偲偡傞偲丄
丂俹乫俫乫亖倲/![]() 丂側偺偱丄
丂側偺偱丄
丂俽乮倲乯亖兾乮倲2亅俀倲亄俀乯亅兾倲2/俀亖兾乮倲2亅係倲亄係乯/俀亖兾乮倲亅俀乯2/俀
乮俀乯丂媮傔傞俲偺懱愊偼丄
丂佺02 俽乮倲乯倓倲亖乮兾/俀乯乮佺01 倲2倓倲亄佺12 乮倲亅俀乯2倓倲乯亖兾/俁丂丂乮廔乯
乮僐儊儞僩乯丂戣堄傪枮偨偡奊偑昤偗傞偐偳偆偐偑億僀儞僩偱偡偹両
乮捛婰乯丂椷榓俈擭俉寧俋擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俈乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂娭悢 倷亖倶亅併乮倶亄俀乯丂乮倶亞亅俀乯丂傪峫偊傞丅
乮侾乯丂偙偺娭悢偺嵟彫抣偲丄僌儔僼偲嵗昗幉偲偺岎揰傪媮傔丄倷亖倶亅併乮倶亄俀乯偺僌儔僼偺
丂丂奣宍傪偐偗丅
乮俀乯丂偙偺娭悢偺僌儔僼偲丄捈慄 倶亖亅俀 偍傛傃 倶 幉偱埻傑傟偨恾宍傪丄倶 幉偺廃傝偵侾夞
丂丂揮偟偰偱偒傞棫懱偺懱愊倁傪媮傔傛丅
乮夝乯乮侾乯丂倷乫亖侾亅侾/乮俀併乮倶亄俀乯乯亖乮俀併乮倶亄俀乯亅侾乯/乮俀併乮倶亄俀乯乯亖侽丂傛傝丄
丂俀併乮倶亄俀乯亅侾亖侽丂偡側傢偪丄丂倶亖亅俈/係
憹尭昞偼丄
丂丂
丂傛偭偰丄嵟彫抣偼丄亅俋/係丂乮倶亖亅俈/係 偺偲偒乯
丂倶亅併乮倶亄俀乯亖侽丂偡側傢偪丄倶亖併乮倶亄俀乯丂偐傜丄丂倶2亅倶亅俀亖乮倶亅俀乯乮倶亄侾乯亖侽
丂倶亞侽丂傛傝丄丂倶亖俀丂偲側傝丄倶 幉偲偺岎揰偼丄丂乮俀丆侽乯
丂倷亖倶亅併乮倶亄俀乯丂偵偍偄偰丄倶亖侽 偲偍偔偲丄丂倷亖亅![]() 丂偐傜丄
丂偐傜丄
丂倷 幉偲偺岎揰偼丄丂乮侽丆亅![]() 乯
乯
丂倷亖倶亅併乮倶亄俀乯偺僌儔僼偺奣宍偼壓恾丅
丂丂
乮俀乯丂倁亖兾佺-22 乮倶亅併乮倶亄俀乯乯2倓倶亖兾佺-22 乮倶2亄倶亄俀亅俀倶併乮倶亄俀乯乯倓倶
丂亖兾佺-22 乮倶2亄倶亄俀乯倓倶亅俀兾佺-22 倶併乮倶亄俀乯乯倓倶
偙偙偱丄丂佺-22 乮倶2亄倶亄俀乯倓倶亖俀佺02 乮倶2亄俀乯倓倶亖係侽/俁
丂佺-22 倶併乮倶亄俀乯乯倓倶
亖[乮俀倶/俁乯乮倶亄俀乯丱乮俁/俀乯]-22亅乮係/侾俆乯[乮倶亄俀乯丱乮俆/俀乯]-22亖俁俀/侾俆
側偺偱丄丂倁亖乮係侽/俁乯兾亅俀兾乮俁俀/侾俆乯亖乮侾俁俇/侾俆乯兾丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾侽寧俆擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮俀侽侽侽乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂 嬋慄 倷亖倰倕倰倶 (倰偼惓偺掕悢)忋偺揰俹乮倎丆倐乯偵偍偗傞愙慄偑尨揰傪捠傞偲偡傞丅
丂丂揰俹傪捠傝丄倷幉偵暯峴側捈慄丄倶幉丄倷幉偍傛傃嬋慄 倷亖倰倕倰倶 偵傛偭偰埻傑傟傞晹暘傪
丂丂俽偲偟丄俽傪倶幉偺傑傢傝偵侾夞揮偟偰偱偒傞夞揮懱偺懱愊傪倁1丄俽傪倷幉偺傑傢傝偵侾夞
丂丂揮偟偰偱偒傞夞揮懱偺懱愊傪倁2偲偡傞丅
乮侾乯丂倎丄倐 傪 倰 傪梡偄偰昞偣丅
乮俀乯丂倁1亖倁2 偲側傞傛偆側 倰 偺抣傪媮傔傛丅
乮夝乯乮侾乯丂揰俹乮倎丆倐乯偵偍偗傞愙慄偺曽掱幃偼丄丂倷亖倰2倕倰倎乮倶亅倎乯亄倰倕倰倎
尨揰傪捠傞偺偱丄丂倰2倕倰倎乮亅倎乯亄倰倕倰倎亖侽丂傛傝丄丂亅倎倰亄侾亖侽丂丂傛偭偰丄丂a亖侾/倰
偙偺偲偒丄丂倐亖倰倕倰倎亖倰倕
乮俀乯丂倁1亖兾佺0a 倰2倕2rx倓倶亖兾倰2佺0a 倕2rx亖乮兾倰/俀乯乵倕2rx乶0a亖乮兾倰/俀乯乮倕2亅1乯
丂倁2亖兾乮侾/倰乯2丒倰倕亅兾佺rre 倶2倓倷亖兾倕/倰亅兾佺01/r 倶2倰2倕倰倶倓倶
丂亖兾倕/倰亅兾倰2佺01/r 倶2倕倰倶倓倶
偙偙偱丄
佺01/r 倶2倕倰倶倓倶亖乵乮倶2/倰乯倕rx乶01/r亅乮俀/倰乯佺01/r 倶倕倰倶倓倶
亖倕/倰3亅乮俀/倰乯乮乵乮倶/倰乯倕rx乶01/r亅乮侾/倰乯佺01/r 倕倰倶倓倶乯
亖倕/倰3亅乮俀/倰乯乮倕/倰2亅乮侾/倰2乯乮倕亅侾乯乯
亖乮倕亅俀乯/倰3
側偺偱丄丂倁2亖兾倕/倰亅兾乮倕亅俀乯/倰亖俀兾/倰
丂倁1亖倁2 偐傜丄丂乮兾倰/俀乯乮倕2亅1乯亖俀兾/倰丂傛傝丄丂倰2亖係/乮倕2亅1乯
傛偭偰丄丂倰亖俀/併乮倕2亅1乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾侾寧俀係擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮俀侽侽俁乯偺栤戣傕夞揮懱偺懱愊偺寁嶼偱偁傞丅
栤戣丂丂 倶倷倸嬻娫撪偵俀揰P(倳丆倳丆侽)丄俻(倳丆侽丆併乮侾亅倳2乯)傪峫偊傞丅倳偑侽偐傜侾傑偱摦偔
丂丂偲偒丄慄暘俹俻偑捠夁偟偰偱偒傞嬋柺傪俽偲偡傞丅
乮侾乯丂揰俼(倳丆侽丆侽) 乮侽亝倳亝侾乯偲慄暘俹俻偺嫍棧傪媮傔傛丅
乮俀乯丂嬋柺俽傪倶幉偺傑傢傝偵侾夞揮偝偣偰摼傜傟傞棫懱偺懱愊傪媮傔傛丅
丂丂
乮夝乯乮侾乯丂俹俻亖侾丂傛傝丄丂俼俫亖倳併乮侾亅倳2乯丂偱偁傞丅
乮俀乯丂倳亖併乮侾亅倳2乯丂傛傝丄丂倳亖侾/![]() 丂側偺偱丄
丂側偺偱丄
丂侽亝倳亝侾/![]() 丂偺偲偒丄丂倳亝併乮侾亅倳2乯
丂偺偲偒丄丂倳亝併乮侾亅倳2乯
丂侾/![]() 亝倳亝侾丂偺偲偒丄丂倳亞併乮侾亅倳2乯
亝倳亝侾丂偺偲偒丄丂倳亞併乮侾亅倳2乯
傛偭偰丄媮傔傞懱愊偼丄
兾佺01/![]() 乮侾亅倳2亅倳2乮侾亅倳2乯乯倓倳亄兾佺1/
乮侾亅倳2亅倳2乮侾亅倳2乯乯倓倳亄兾佺1/![]() 1 乮倳2亅倳2乮侾亅倳2乯乯
1 乮倳2亅倳2乮侾亅倳2乯乯
亖兾佺01/![]() 乮侾亅倳2乯倓倳亄兾佺1/
乮侾亅倳2乯倓倳亄兾佺1/![]() 1 倳2倓倳亅兾佺01 倳2乮侾亅倳2乯倓倳
1 倳2倓倳亅兾佺01 倳2乮侾亅倳2乯倓倳
亖兾[倳亅倳3/俁]01/![]() 亄兾[倳3/俁]1/
亄兾[倳3/俁]1/![]() 1亅兾[倳3/俁亅倳5/俆]01
1亅兾[倳3/俁亅倳5/俆]01
亖乮俆/侾俀乯![]() 兾亄乮侾/俁亅乮侾/侾俀乯
兾亄乮侾/俁亅乮侾/侾俀乯![]() 乯兾亅乮俀/侾俆乯兾
乯兾亅乮俀/侾俆乯兾
亖乮侾/俆亄![]() /俁乯兾丂丂乮廔乯
/俁乯兾丂丂乮廔乯
丂丂埲壓丄岺帠拞両