１３１	令和５年度前期	京都大学	文系	・・・	ベクトル（数学Ｂ）	標準

京都大学　前期文系（２０２３）

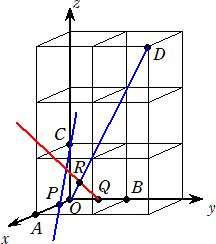
第２問　空間内の４点Ｏ、A、B、Cは同一平面上にないとする。点Ｄ、P、Qを次のように定め
　　る。点Dは ＯＤ＝OA＋２OB＋３OC を満たし、点Pは線分OAを １：２ に内分し、点Qは線
　　分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように
　　定める。このとき、線分ORの長さと線分RDの長さの比 ＯR ： RD を求めよ。

　　

＃理系（２０２３）と共通問題でした。

（解）　題意より、　ＯＰ＝（１/３）ＯＡ　、ＯＱ＝（１/２）ＯＢ　である。

　また、直線QRと直線PCが交点を持つので、　（１/２）ＯＢ＋ｓＲＱ＝ＯＰ＋ｔＰＣ　となる実数

ｓ、ｔ が存在する。すなわち、

　（１/２）ＯＢ＋ｓ（（１/２）ＯＢ−ＯＲ）＝（１/３）ＯＡ＋ｔ（ＯＣ−（１/３）ＯＡ）　より、

　ｓＯＲ＝｛（ｔ−１）/３｝ＯＡ＋｛（１＋ｓ）/２｝ＯＢ−ｔＯＣ

ここで、Ｒは直線ＯＤ上にあるので、ＯＲ＝ｋOA＋２ｋOB＋３ｋOC となる実数ｋが存在する。

よって、　ｋｓOA＋２ｋｓOB＋３ｋｓOC＝｛（ｔ−１）/３｝ＯＡ＋｛（１＋ｓ）/２｝ＯＢ−ｔＯＣ

空間内の４点Ｏ、A、B、Cは同一平面上にないので、OA、OB、OCは１次独立である。

よって、　ｋｓ＝（ｔ−１）/３　、２ｋｓ＝（１＋ｓ）/２　、３ｋｓ＝−ｔ

第１式と第３式から、　ｔ−１＝−ｔ　なので、　ｔ＝１/２　より、　ｋｓ＝−１/６

よって、第２式より、　（１＋ｓ）/２＝−１/３　なので、　ｓ＝−５/３

したがって、　ｋ＝１/１０　となるので、　ＯR ： RD＝１ ： ９ である。　　（終）



　　以下、工事中！