| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侾俀俉 | 椷榓俆擭搙慜婜 | 丂搶嫗戝妛丂 | 丂暥宯 | 丒丒丒 | 丂恾宍偲寁検乮悢嘥丒俙乯 | 丂傗傗擄 |
搶嫗戝妛丂慜婜暥宯乮俀侽俀俁乯
戞係栤丂敿宎侾偺媴柺忋偺憡堎側傞係揰A丄B丄C丄D 偑丄AB亖侾丄AC亖BC丄AD亖BD丄
丂丂cos佢ACB亖cos佢ADB亖係/俆 傪枮偨偟偰偄傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂仮ABC偺柺愊傪媮傔傛丅
乮俀乯丂巐柺懱ABCD偺懱愊傪媮傔傛丅
仈戣堄傛傝丄俙俛丄俠俢偺拞揰傪偦傟偧傟俵丄俶偲偍偔偲丄慄暘俵俶忋偵丄媴偺拞怱俷偑偁傞丅
丂丂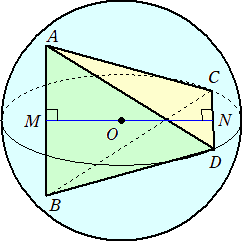
乮夝乯(1)丂cos佢ACB亖係/俆丂傛傝丄丂倱倝値佢AC俛亖俁/俆
丂傑偨丄仮俙俛俠偼俀摍曈嶰妏宍偱丄捈妏嶰妏宍俙俠俵偵偍偄偰丄
丂倱倝値2佢AC俵亖乮侾亅cos佢ACB乯/俀亖侾/侾侽丂傛傝丄丂倱倝値佢AC俵亖侾/![]()
傛偭偰丄丂俙俠丒倱倝値佢AC俵亖俙俵亖侾/俀丂傛傝丄丂俙俠亖![]() /俀
/俀
丂埲忋偐傜丄丂仮俙俛俠亖乮侾/俀乯丒乮![]() /俀乯丒乮
/俀乯丒乮![]() /俀乯丒乮俁/俆乯亖俁/係
/俀乯丒乮俁/俆乯亖俁/係
乮俀乯丂俠俵2亖俙俠2亅乮侾/俀乯2亖俆/俀亅侾/係亖俋/係丂傛傝丄丂俠俵亖俁/俀
丂傑偨丄丂俷俵2亖侾2亅乮侾/俀乯2亖俁/係丂傛傝丄丂俷俵亖![]() /俀
/俀
丂偙偺偲偒丄丂俠俵2亅乮俷俶亄俷俵乯2亖俷俠2亅俷俶2丂傛傝丄
丂俋/係亅乮俷俶亄![]() /俀乯2亖侾2亅俷俶2丂傪夝偄偰丄丂俷俶亖
/俀乯2亖侾2亅俷俶2丂傪夝偄偰丄丂俷俶亖![]() /俇
/俇
傛偭偰丄丂俵俶亖![]() /俀亄
/俀亄![]() /俇亖俀
/俇亖俀![]() /俁
/俁
偝傜偵丄丂俠俢亖俀俠俶亖俀併乮侾亅侾/侾俀乯亖![]() /
/![]() 丂側偺偱丄
丂側偺偱丄
丂巐柺懱ABCD偺懱愊偼丄
丂乮侾/俀乯丒乮![]() /
/![]() 乯丒乮俀
乯丒乮俀![]() /俁乯丒侾丒乮侾/俁乯亖
/俁乯丒侾丒乮侾/俁乯亖![]() /俋丂丂乮廔乯
/俋丂丂乮廔乯
乮僐儊儞僩乯丂媣偟傇傝偺棫懱恾宍偱偟偨丅
丂丂埲壓丄岺帠拞両丂