| |
||||||
| １２１ | 令和６年度前期 | 東京医科歯科大学 | 理系 | ・・・ | ベクトル（数学Ｂ） | 標準 |
東京医科歯科大学 前期理系（２０２４）
第２問 ｘｙｚ 空間において、点A(１，０，０）、B(０，１，０)、C(−１，０，０)、D(０，０，１)をとり、
線分CDの中点をMとする。さらに、Nを線分BD上の点とする。また、ｚ 軸と平行でない直
線上の異なる２点P(ｘ，ｙ，ｚ)、Q(ｘ’，ｙ’，ｚ’)に対して、
（ｚ’−ｚ）/√（（ｘ’−ｘ）2＋（ｙ’−ｙ）2）
をベクトルＰＱの勾配と呼ぶ。ＡＮの勾配を ｔ1、ＮＭの勾配を ｔ2 とするとき、以下の各問い
に答えよ。
（１） ｔ2 ＝０ となるようにNをとったとき、ｔ1 の値を求めよ。
（２） Ｌ＝｜ＡＮ｜＋｜ＮＭ｜とし、Ｌが最小となるようにNをとったとき、Ｌの値を求めよ。
（３） ０≦ｔ2≦ｔ1 となるようにNをとったとき、Nの ｙ 座標を s とする。s がとり得る値の範囲
を求めよ。
（解）（１） Ｍ（−１/２，０，１/２）で、ｔ2 ＝０ より、Ｎ（０，１/２，１/２）なので、
ｔ1 ＝（１/２）/√｛（−１）2＋（１/２）2｝＝（１/２）/（
/２）＝１/
（２） 図形ＡＢＣＤの展開図において、３点Ａ、Ｎ、Ｍが１直線上にあるとき、Ｌは最小となる。
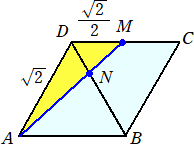
したがって、
Ｌ2＝（
）2＋（/２）2−２・・（/２）ｃｏｓ１２０°＝２＋１/２＋１＝７/２
より、 Ｌ＝
/２
（３） A(１，０，０）、Ｎ（０，ｓ，１−ｓ）、Ｍ（−１/２，０，１/２）より、
０≦（ｓ−１/２）/√｛（１/２）2＋ｓ2｝≦（１−ｓ）/√（１＋ｓ2）
よって、 １/２≦ｓ≦１ で、 （ｓ−１/２）2/｛（１/４）＋ｓ2｝≦（１−ｓ）2/（１＋ｓ2）
すなわち、 （ｓ−１/２）2（１＋ｓ2）≦（１−ｓ）2｛（１/４）＋ｓ2｝ から、ｓ3−（１/２）ｓ≦０
これを解いて、 ｓ≦−１/、０≦ｓ≦１/
これと、１/２≦ｓ≦１ を合わせて、求める s がとり得る値の範囲は、
１/２≦ｓ≦１/ （終）
以下、工事中！