１１８	令和６年度前期	一橋大学	文系	・・・	ベクトル（数学Ｂ）	標準

一橋大学　前期文系（２０２４）

第４問　実数 ａ、ｂ は −１＜ａ＜１、−１＜ｂ＜１ を満たす。座標空間内に４点A(ａ，−１，−１)、
　　B(−１，ｂ，−１)、C(−ａ，１，１)、D(１，−ｂ，１)をとる。

（１）　A、B、C、D がひし形の頂点となるとき、ａ と ｂ の関係を表す等式を求めよ。
（２）　ａ、ｂ が（１）の等式を満たすとき、A、B、C、D を頂点とする四角形の面積の最小値を
　　求めよ。

（解）（１）　ＡＢＣＤ で、ＡＢ＝ＣＤ なので、四角形ＡＢＣＤは平行四辺形である。

　平行四辺形ＡＢＣＤがひし形となるためには、　ＡＣ⊥ＢＤ

ここで、　ＡＣ＝（−２ａ，２，２）　、ＢＤ＝（２，−２ｂ，２）　なので、

　ＡＣ・ＢＤ＝−４ａ−４ｂ＋４＝０　から、　ａ＋ｂ−１＝０

（２）　ひし形ＡＢＣＤの面積は、　ＡＣ・ＢＤ/２　で求められる。

（ＡＣ・ＢＤ/２）²＝（４ａ²＋８）（４ｂ²＋８）/４＝（４ａ²＋８）（ｂ²＋２）

ｂ＝１−ａ　を代入して、

　（ＡＣ・ＢＤ/２）²＝（４ａ²＋８）（（１−ａ）²＋２）＝（４ａ²＋８）（ａ²−２ａ＋３）

ここで、　ｙ＝（４ａ²＋８）（ａ²−２ａ＋３）　とおくと、

　ｙ’＝８ａ（ａ²−２ａ＋３）＋（４ａ²＋８）（２ａ−２）

　＝１６ａ³−２４ａ²＋４０ａ−１６＝１６（ａ−１/２）（ａ²−ａ＋２）

　ａ²−ａ＋２＞０　なので、　ｙ’＝０　を解くと、　ａ＝１/２

　よって、増減表は、

　

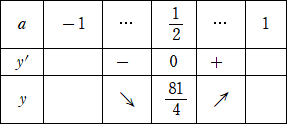
したがって、ａ＝１/２ のとき、ｙ は極小かつ最小で、最小値は、８１/４　となるので、

求める四角形の面積の最小値は、　９/２　　（終）



　　以下、工事中！