１１０	令和６年度前期	九州大学	理系	・・・	ベクトル（数学Ｂ）	標準

九州大学　前期理系（２０２４）

第１問　ａ を実数とし、座標空間内の３点P(−１，１，−１)、Q(１，１，１)、R(ａ，ａ²，ａ³) を考
　　える。以下の問いに答えよ。　
（１）　ａ≠−１、ａ≠１ のとき、３点P、Q、R は一直線上にないことを示せ。
（２）　ａ が−１＜ａ＜１の範囲を動くとき、△PQRの面積の最大値を求めよ。

（解）（１）　ＰＱ＝（２，０，２）　、ＰＲ＝（ａ＋１，ａ²−１，ａ³＋１）

　ａ≠−１、ａ≠１ より、ａ²−１≠０　なので、　ＰＲ＝ｋＰＱ　となる実数ｋは存在しない。

　よって、３点P、Q、R は一直線上にない。

（２）　ＰＱ＝２　で、直線ＰＱの方程式は、ｘ＝ｚ　、ｙ＝１　なので、直線ＰＱ上の点Ｓは、

　Ｓ（ｔ，１，ｔ）　と書ける。　ＳＲ＝（ｔ−ａ，１−ａ²，ｔ−ａ³）　で、ＳＲ⊥ＰＱ　から、

　２（ｔ−ａ）＋２（ｔ−ａ³）＝０　より、　ｔ＝（ａ＋ａ³）/２

このとき、　ＳＲ＝（（−ａ＋ａ³）/２，１−ａ²，（ａ−ａ³）/２）　なので、

　ＳＲ²＝（−ａ＋ａ³）²/４＋（１−ａ²）²＋（ａ−ａ³）²/４＝（１−ａ²）²（ａ²＋２）/２

ここで、　ｙ＝（１−ａ²）²（ａ²＋２）　とおくと、

　ｙ’＝２（１−ａ²）（−２ａ）（ａ²＋２）＋２ａ（１−ａ²）²＝−６ａ（１−ａ²）（１＋ａ²）

　ａ が−１＜ａ＜１の範囲を動くとき、増減表は、

　　

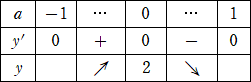
となるので、ＳＲ²は、ａ＝０のとき、極大かつ最大で、最大値２/２＝１ となる。

　したがって、△PQRの面積の最大値は、　（１/２）・２・１＝　である。　　（終）



　　以下、工事中！