１０８	令和６年度前期	名古屋大学	理系	・・・	ベクトル（数学Ｂ）	標準

名古屋大学　前期理系（２０２４）

第３問　座標空間の３点 A(３，１，３)、B(４，２，２)、C(４，０，１) の定める平面をHとする。
　　また、AP＝sAB＋ｔAC (ｓ、ｔ は非負の実数) を満たすすべての点Pからなる領域をKと
　　する。
（１）　内積 AB・AB、AC・AC、AB・AC を求めよ。
（２）　原点Ｏ(０，０，０)から平面Ｈに下ろした垂線の足をQとする。AQをABとACで表せ。
（３）　領域Ｋ上の点Pに対して、線分QP上の点で AR＝rAC （r は非負の実数)を満たす
　点Rが存在することを示せ。
（４）　領域Ｋにおいて原点Ｏからの距離が最小となる点Sの座標を求めよ。

（解）（１）　AB＝（１，１，−１）、AC＝（１，−１，−２）　より、

　AB・AB＝１＋１＋１＝３　、AC・AC＝１＋１＋４＝６　、AB・AC＝１−１＋２＝２

（２）　AQ＝sAB＋ｔAC　とおくと、

　ＯQ＝ＯＡ＋AQ＝（ｓ＋ｔ＋３，ｓ−ｔ＋１，−ｓ−２ｔ＋３）

　題意より、　ＯQ⊥AB　、ＯQ⊥AＣ　なので、

ＯQ・AB＝３ｓ＋２ｔ＋１＝０　、ＯQ・AC＝ｓ＋３ｔ−２＝０

これを解いて、　ｔ＝１、ｓ＝−１　なので、　AQ＝−AB＋AC

（３）　点Ｐは、AP＝sAB＋ｔAC (ｓ、ｔ は非負の実数) を満たす。

　点Ｘを線分ＱＰ上の点とすると、　ＱＸ＝ｋＱＰ　（０≦ｋ≦１）　と書ける。

このとき、Ｘは線分ＱＰを ｋ ： １−ｋ に内分する点なので、ＡＸ＝（１−ｋ）ＡＱ＋ｋＡＰ

すなわち、

ＡＸ＝（１−ｋ）（−AB＋AC）＋ｋ（sAB＋ｔAC）＝（（ｓ＋１）ｋ−１）AB＋（（ｔ−１）ｋ＋１）AC

そこで、ｋ＝１/（ｓ＋１）　とおくと、０≦ｋ≦１　を満たし、

　ＡＸ＝（（ｔ−１）/（ｓ＋１）＋１）AC＝（ｔ＋ｓ）/（ｓ＋１）AC

このとき、ｒ＝（ｔ＋ｓ）/（ｓ＋１）　とおくと、ｒ は非負の実数で、AR＝rAC を満たす線分QP上

の点Ｒが存在することを示す。

（４）　（２）より、ＡＱ＝ＢＣ　なので、下図を得る。

　　

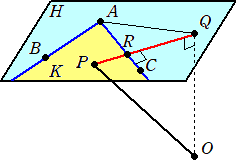
ＯＰ²＝ＯＱ²＋ＱＲ² で、ＯＱは一定なので、ＯＰが最小となるのは、ＱＰが最小の時である。

Ｑから直線ＡＣに垂線を下ろし、その足をＲとおく。（３）より、AR＝rAC を満たす非負の実数

ｒ が存在する。このとき、　ＱＲ⊥ＡＣ より、　（ＡＲ−ＡＱ）・ＡＣ＝０

すなわち、　（ｒＡＣ＋ＡＢ−ＡＣ）・ＡＣ＝０　より、　６ｒ＋２−６＝０　を解いて、　ｒ＝２/３

　このとき、　AR＝（２/３）AC＝（２/３，−２/３，−４/３）　より、Ｒ（１１/３，１/３，５/３）で、

ＲはＫ上の点である。

　したがって、領域Ｋにおいて原点Ｏからの距離が最小となる点Sの座標は、

　Ｓ（１１/３，１/３，５/３）

である。　　（終）



　　以下、工事中！