| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侾侽係 | 椷榓俇擭搙慜婜 | 丂戝嶃戝妛丂 | 丂棟宯 | 丒丒丒 | 丂夞揮懱偺懱愊乮悢妛嘨乯 | 丂昗弨 |
戝嶃戝妛丂慜婜棟宯乮俀侽俀係乯
戞係栤丂倎亜侾偲偡傞丅倶倷暯柺偵偍偄偰丄揰(倎丆侽)傪拞怱偲偡傞敿宎侾偺墌傪C偲偡傞丅
丂丂乮侾乯丂墌俠偺 倶亞倎 偺晹暘偲 倷 幉偍傛傃俀捈慄 倷亖侾丄倷亖亅侾 偱埻傑傟偨恾宍傪 倷 幉偺
丂丂丂傑傢傝偵侾夞挔偟偰偱偒傞夞揮懱偺懱愊倁1傪媮傔傛丅
丂丂乮俀乯丂墌C偱埻傑傟偨恾宍傪 倷 幉偺傑傢傝偵侾夞揮偟偰偱偒傞夞揮懱偺懱愊傪V2偲偡傞丅
丂丂丂乮侾乯偵偍偗傞倁1偵偮偄偰丄倁1亖俀倁2 偲側傞 倎 偺抣傪媮傔傛丅
丂丂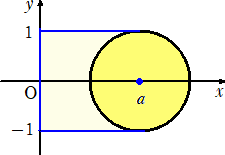
乮夝乯乮侾乯丂墌俠偺曽掱幃偼丄丂乮倶亅倎乯2亄倷2亖侾丂偡側傢偪丄丂倶亖倎亇併乮侾亅倷2乯
丂傛偭偰丄
倁1亖兾佺-11 倶2倓倷亖俀兾佺01 乮倎亄併乮侾亅倷2乯乯2倓倷
丂亖俀兾佺01 乮倎2亄侾亅倷2亄俀倎併乮侾亅倷2乯乯倓倷
丂亖俀兾乮倎2亄侾亅侾/俁亄俀倎丒兾/係乯
丂亖兾乮俀倎2亄係/俁亄倎丒兾乯
乮俀乯丂倁2亖倁1亅俀兾佺01 乮倎2亄侾亅倷2亅俀倎併乮侾亅倷2乯乯倓倷
丂亖兾乮俀倎2亄係/俁亄倎丒兾乯亅俀兾乮倎2亄侾亅侾/俁亅俀倎丒兾/係乯
丂亖兾乮俀倎2亄係/俁亄倎丒兾乯亅兾乮俀倎2亄係/俁亅倎丒兾乯
丂亖俀倎兾2
忦審傛傝丄倁1亖俀倁2 側偺偱丄丂兾乮俀倎2亄係/俁亄倎丒兾乯亖係倎兾2丂傛傝丄
丂俀倎2亄係/俁亅俁倎丒兾亖侽丂偡側傢偪丄丂俇倎2亅俋倎丒兾亄係亖侽丂側偺偱丄
丂倎亖乮俋兾亇併乮俉侾兾2亅俋俇乯乯/侾俀
偙偙偱丄俥乮倎乯亖俇倎2亅俋倎丒兾亄係丂偲偍偔偲丄丂俥乮侾乯亖侾侽亅俋兾亙侽丂側偺偱丄
丂俥乮倎乯亖侽丂偼丄侾傛傝戝偒偄夝偲侾傛傝彫偝偄夝傪帩偮丅
丂倎亜侾 側偺偱丄丂倎亖乮俋兾亄併乮俉侾兾2亅俋俇乯乯/侾俀丂偱偁傞丅丂丂乮廔乯
丂丂埲壓丄岺帠拞両丂