| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俋俋 | 椷榓俇擭搙慜婜 | 丂搶嫗岺嬈戝妛丂 | 丂棟宯 | 丒丒丒 | 丂悢楍丒嬌尷乮悢俛丒嘨乯 | 丂昗弨 |
搶嫗岺嬈戝妛丂慜婜棟宯乮俀侽俀係乯
戞俁栤丂倶倷 暯柺忋偵丄揰A乮倎丆侽乯丄B(侽丆倐乯丄C(亅倎丆侽)丂(偨偩偟丄侽亙倎亙倐乯 傪偲傞丅揰A丄
丂丂B傪捠傞捈慄傪俴偲偟丄揰C傪捠傝慄暘BC偵悅捈側捈慄傪俲偲偡傞丅
丂偝傜偵丄揰A傪捠傝 倷 幉偵暯峴側捈慄偲捈慄俲偲偺岎揰傪C1偲偟丄揰G傪捠傝 倶 幉偵暯峴側
捈慄偲捈慄俴偲偺岎揰傪A1偲偡傞丅埲壓丄値亖侾丄俀丄俁丄丒丒丒丂偵懳偟偰丄揰A値傪捠傝 倷 幉偵
暯峴側捈慄偲捈慄俲偲偺岎揰傪Cn+1丄揰Cn+1傪捠傝 倶 幉偵暯峴側捈慄偲捈慄俴偲偺岎揰傪
An+1偲偡傞丅
丂丂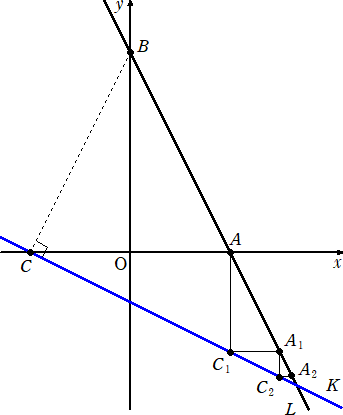
乮侾乯丂揰A値丄C値 偺嵗昗傪媮傔傛丅
乮俀乯丂仮CBA値偺柺愊S値傪媮傔傛丅
乮俁乯丂倢倝倣値仺亣 俛俙値/俛俠 傪媮傔傛丅
乮夝乯乮侾乯丂捈慄俴偺曽掱幃偼丄倷亖亅乮倐/倎乯倶亄倐丂偱丄
丂捈慄俲偺曽掱幃偼丄倷亖亅乮倎/倐乯乮倶亄倎乯丂偲側傞丅
丂偙偺偲偒丄丂俠1乮倎丆亅俀倎2/倐乯丂丄俙1乮倎乮俀倎2亄倐2乯/倐2丆亅俀倎2/倐乯丂偱偁傞丅
丂俠値乮倶値丆倷値乯丂偲偍偔偲丄倷値亖亅乮倎/倐乯乮倶値亄倎乯丂偱丄
丂俙値乮乮倎/倐乯2乮倶値亄倎乯亄倎丆亅乮倎/倐乯乮倶値亄倎乯乯
側偺偱丄丂俠値+1乮乮倎/倐乯2乮倶値亄倎乯亄倎丆亅乮倎/倐乯3乮倶値亄倎乯亅俀倎2/倐乯
丂埲忋偐傜丄丂倶値+1亖乮倎/倐乯2乮倶値亄倎乯亄倎丂偑惉傝棫偮丅
丂倶値+1亅乮倐2亄倎2乯倎/乮倐2亅倎2乯亖乮倎/倐乯2乮倶値亅乮倐2亄倎2乯倎/乮倐2亅倎2乯乯丂丄倶1亖倎丂偐傜丄
丂倶値亅乮倐2亄倎2乯倎/乮倐2亅倎2乯亖乮倎亅乮倐2亄倎2乯倎/乮倐2亅倎2乯乯乮倎/倐乯2値-2
傛偭偰丄丂倶値亖乮倐2亄倎2乯倎/乮倐2亅倎2乯亅俀倎3/乮倐2亅倎2乯丒乮倎/倐乯2値-2
丂偙偺偲偒丄俠値偺 倷 嵗昗倷値偼丄
倷値亖亅乮倎/倐乯乮乮倐2亄倎2乯倎/乮倐2亅倎2乯亅俀倎3/乮倐2亅倎2乯丒乮倎/倐乯2値-2亄倎乯
丂亖亅乮倐2亄倎2乯倎2/乮倐乮倐2亅倎2乯乯亄俀倎3/乮倐2亅倎2乯丒乮倎/倐乯2値-1亅倎2/倐
丂亖亅俀倎2倐/乮倐2亅倎2乯亄俀倎3/乮倐2亅倎2乯丒乮倎/倐乯2値-1
丂亖亅俀倎2倐/乮倐2亅倎2乯亄俀倎2倐/乮倐2亅倎2乯丒乮倎/倐乯2値
丂亖俀倎2倐/乮倐2亅倎2乯丒乮乮倎/倐乯2値亅侾乯
丂摨條偵偟偰丄俙値乮倳値丆倴値乯丂偲偍偔偲丄
丂倳値亖乮倎/倐乯2乮倶値亄倎乯亄倎
丂亖乮倐2亄倎2乯倎3/乮倐2乮倐2亅倎2乯乯亅俀倎3/乮倐2亅倎2乯丒乮倎/倐乯2値亄倎3/倐2亄倎
丂亖倎乮倐2亄倎2乯/乮倐2亅倎2乯亅俀倎3/乮倐2亅倎2乯丒乮倎/倐乯2値
丂倴値亖亅乮倎/倐乯乮倶値亄倎乯
丂亖亅俀倎2倐/乮倐2亅倎2乯亄俀倎3/乮倐2亅倎2乯丒乮倎/倐乯2値-1
丂亖亅俀倎2倐/乮倐2亅倎2乯亄俀倎2倐/乮倐2亅倎2乯丒乮倎/倐乯2値
丂亖俀倎2倐/乮倐2亅倎2乯丒乮乮倎/倐乯2値亅侾乯
乮俀乯丂仮CBA値亖仮俠俛俙丒乮俛俙値/俛俙乯亖仮俠俛俙丒乮倳値/倎乯
丂乮侾乯傛傝丄倳値亖倎乮倐2亄倎2乯/乮倐2亅倎2乯亅俀倎3/乮倐2亅倎2乯丒乮倎/倐乯2値丂側偺偱丄
丂倳値/倎亖乮倐2亄倎2乯/乮倐2亅倎2乯亅俀倎2/乮倐2亅倎2乯丒乮倎/倐乯2値
丂傑偨丄仮俠俛俙亖倎倐丂側偺偱丄
丂俽値亖倎倐乮倐2亄倎2乯/乮倐2亅倎2乯亅俀倎3倐/乮倐2亅倎2乯丒乮倎/倐乯2値
偲側傞丅
乮俁乯丂乮俀乯偲摨條偵偟偰丄俛俠亖俛俙丂側偺偱丄丂俛俙値/俛俠亖俛俙値/俛俙亖倳値/倎
偙偙偱丄丂倳値/倎亖乮倐2亄倎2乯/乮倐2亅倎2乯亅俀倎2/乮倐2亅倎2乯丒乮倎/倐乯2値
丂忦審傛傝丄侽亙倎亙倐丂側偺偱丄丂侽亙倎/倐亙侾
傛偭偰丄丂値 仺 亣丂偺偲偒丄丂乮倎/倐乯2値仺 侽丂側偺偱丄
丂倢倝倣値仺亣 俛俙値/俛俠 亖乮倐2亄倎2乯/乮倐2亅倎2乯丂丂乮廔乯
乮僐儊儞僩乯丂乮俀乯乮俁乯偲斾傋偰丄乮侾乯偺寁嶼偑戝曄偱偟偨両
丂丂埲壓丄岺帠拞両丂