| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俋俈 | 椷榓俇擭搙慜婜 | 丂搶嫗岺嬈戝妛丂 | 丂棟宯 | 丒丒丒 | 丂旝暘乮悢嘦丒嘨乯 | 丂昗弨 |
搶嫗岺嬈戝妛丂慜婜棟宯乮俀侽俀係乯
戞侾栤丂倶倷 暯柺忋偺嬋慄 倷亖乮侾/俀乯倶2 偵丄揰乮倎丆乮侾/俀乯倎2乯偱愙偡傞墌偺偆偪丄倷 幉偺惓偺
丂丂晹暘偵傕愙偡傞傕偺傪俽倎偲偍偔丅倎 偑惓偺幚悢傪摦偔偲偒偺俽倎偺拞怱偺婳愓傪C丄摿偵俽1
丂丂偺拞怱傪P偲偡傞丅
丂丂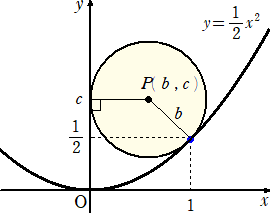
乮侾乯丂揰俹偺嵗昗傪媮傔傛丅
乮俀乯丂揰俹偵偍偗傞嬋慄C偺愙慄偺孹偒傪媮傔傛丅
乮夝乯乮侾乯丂戣堄傛傝丄墌俽1偺拞怱俹乮倐丆們乯偲偍偔偲丄敿宎偼丄倐 偱偁傞丅
丂傛偭偰丄乮倐丆們乯偲乮侾丆侾/俀乯偺嫍棧偑倐傛傝丄丂乮倐亅侾乯2亄乮們亅侾/俀乯2亖倐2
丂偡側傢偪丄亅俀倐亄侾亄們2亅們亄侾/係亖侽丂傛傝丄丂們2亅們亄俆/係亖俀倐
丂傑偨丄倷乫亖倶丂傛傝丄揰乮侾丆侾/俀乯偵偍偗傞愙慄偺孹偒偼丄侾側偺偱丄
丂乮們亅侾/俀乯/乮倐亅侾乯亖亅侾丂傛傝丄丂倐亖俁/俀亅們
傛偭偰丄們2亅們亄俆/係亖俁亅俀們丂傛傝丄丂們2亄們亅俈/係亖侽丂側偺偱丄丂們亖乮亅侾亇俀![]() 乯/俀
乯/俀
偙偙偱丄丂們亜侽丂側偺偱丄丂們亖乮亅侾亄俀![]() 乯/俀
乯/俀
偙偺偲偒丄丂倐亖俁/俀亅乮亅侾亄俀![]() 乯/俀亖乮係亅俀
乯/俀亖乮係亅俀![]() 乯/俀亖俀亅
乯/俀亖俀亅![]()
丂埲忋偐傜丄丂俹乮俀亅![]() 丆乮亅侾亄俀
丆乮亅侾亄俀![]() 乯/俀乯丂偱偁傞丅
乯/俀乯丂偱偁傞丅
乮俀乯丂乮侾乯偲摨條偵偟偰丄丂乮倐亅倎乯2亄乮們亅乮侾/俀乯倎2乯2亖倐2
偡側傢偪丄亅俀倎倐亄倎2亄們2亅倎2們亄乮侾/係乯倎4亖侽丂傛傝丄們2亅倎2們亄倎2亄乮侾/係乯倎4亖俀倎倐
傑偨丄倷乫亖倶丂傛傝丄揰乮倎丆乮侾/俀乯倎2乯偵偍偗傞愙慄偺孹偒偼丄倎 側偺偱丄
丂乮們亅乮侾/俀乯倎2乯/乮倐亅倎乯亖亅侾/倎丂傛傝丄丂倐亖乮侾亅們乯倎亄乮侾/俀乯倎3
傛偭偰丄們2亅倎2們亄倎2亄乮侾/係乯倎4亖俀乮侾亅們乯倎2亄倎4 傛傝丄們2亄倎2們亅倎2亅乮俁/係乯倎4亖侽
偙偺偲偒丄丂們亖乮亅倎2亇俀倎併乮倎2亄侾乯乯/俀
偙偙偱丄丂們亜侽丂側偺偱丄丂們亖乮亅倎2亄俀倎併乮倎2亄侾乯乯/俀亖亅乮侾/俀乯倎2亄倎併乮倎2亄侾乯
偙偺偲偒丄丂倐亖乮侾亄乮侾/俀乯倎2亅倎併乮倎2亄侾乯乯倎亄乮侾/俀乯倎3亖倎亄倎3亅倎2併乮倎2亄侾乯
揰俹偵偍偗傞嬋慄C偺愙慄偺孹偒偼丄
丂倓倐/倓倎亖侾亄俁倎2亅俀倎併乮倎2亄侾乯亅倎3/併乮倎2亄侾乯
丂倎亖侾傪戙擖偟偰丄
丂倓倐/倓倎亖係亅俀![]() 亅侾/
亅侾/![]() 亖乮俉亅俆
亖乮俉亅俆![]() 乯/俀
乯/俀
師偵丄丂倓們/倓倎亖亅倎亄併乮倎2亄侾乯亄倎2/併乮倎2亄侾乯
丂倎亖侾傪戙擖偟偰丄
丂倓們/倓倎亖亅侾亄![]() 亄侾/
亄侾/![]() 亖乮亅俀亄俁
亖乮亅俀亄俁![]() 乯/俀
乯/俀
丂倓們/倓倐亖乮倓們/倓倎乯/乮倓倐/倓倎乯亖乮亅俀亄俁![]() 乯/乮俉亅俆
乯/乮俉亅俆![]() 乯亖侾亄
乯亖侾亄![]() 丂丂乮廔乯
丂丂乮廔乯
乮僐儊儞僩乯丂倓倐/倓倎亖乮俉亅俆![]() 乯/俀丂丄倓們/倓倎亖乮亅俀亄俁
乯/俀丂丄倓們/倓倎亖乮亅俀亄俁![]() 乯/俀丂偲偄偆寢壥偵堦枙偺晄
乯/俀丂偲偄偆寢壥偵堦枙偺晄
丂丂丂丂丂埨傪姶偠傑偟偨偑丄倓們/倓倐亖侾亄![]() 丂偲偄偆旤偟偄寢壥偵姶摦偟傑偟偨両
丂偲偄偆旤偟偄寢壥偵姶摦偟傑偟偨両
丂丂埲壓丄岺帠拞両丂