| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俋俇 | 椷榓俇擭搙慜婜 | 丂搶杒戝妛丂 | 丂棟宯 | 丒丒丒 | 丂旝暘愊暘乮悢妛嘨乯 | 丂擄 |
搶杒戝妛丂慜婜棟宯乮俀侽俀係乯
戞俇栤丂xyz 嬻娫撪偺 xy 暯柺忋偵偁傞墌 C 丗 倶2亄倷2亖侾 偍傛傃墌斅 D 丗 倶2亄倷2亝侾 傪
丂丂峫偊傞丅D傪掙柺偲偟揰P(侽丆侽丆侾)傪捀揰偲偡傞墌悕傪K偲偡傞丅A(侽丆亅侾丆侽)丄B(侽丆侾丆侽)
丂丂偲偡傞丅
丂倶倷倸 嬻娫撪偺暯柺 俫 丗 倸亖倶 傪峫偊傞丅偡側傢偪丄H偼 倶倸 暯柺忋偺捈慄 倸亖倶 偲慄暘AB
傪偲傕偵娷傓暯柺偱偁傞丅K偺懁柺偲H偺岎傢傝偲偟偰偱偒傞嬋慄傪E偲偡傞丅
丂亅兾/俀亝兤亝兾/俀 傪枮偨偡幚悢兤偵懳偟丄墌C忋偺揰Q(cos兤丆sin兤丆侽)傪偲傝丄慄暘PQ
偲E偺嫟桳揰傪R偲偡傞丅
乮侾乯丂慄暘PR偺挿偝傪 倰乮兤乯 偲偍偔丅倰乮兤乯 傪 兤 傪梡偄偰昞偣丅
乮俀乯丂墌悕K偺懁柺偺偆偪丄嬋慄E偺揰A偐傜揰R傑偱傪寢傇晹暘丄慄暘PA丄偍傛傃慄暘PR偵
丂丂傛傝埻傑傟偨晹暘偺柺愊傪S乮兤乯偲偍偔丅兤偲幚悢倛偑忦審 侽亝兤亙兤亄倛亝兾/俀 傪枮
丂丂偨偡偲偒丄師偺晄摍幃偑惉傝棫偮偙偲傪帵偣丅
丂倛乷倰乮兤乯乸2/乮俀![]() 乯亝S乮兤亄倛乯亅S乮兤乯亝倛乷倰乮兤亄倛乯乸2/乮俀
乯亝S乮兤亄倛乯亅S乮兤乯亝倛乷倰乮兤亄倛乯乸2/乮俀![]() 乯
乯
乮俁乯丂墌悕K偺懁柺偺偆偪丄墌C偺 倶亞侽 偺晹暘偲嬋慄E偵傛傝埻傑傟偨晹暘偺柺愊傪俿偲偍
丂偔丅T傪媮傔傛丅昁梫偱偁傟傁 tan乮兤/俀乯亖倳 偲偍偔抲姺愊暘傪梡偄偰傕傛偄丅
丂丂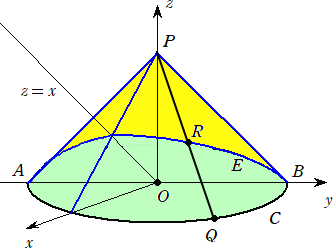
乮夝乯乮侾乯丂捈慄俹俻偺曽掱幃偼丄丂倶/們倧倱兤亖倷/倱倝値兤亖侾亅倸丂側偺偱丄暯柺 倸亖倶 偲偺岎
丂揰俼偺嵗昗偼丄丂倶/們倧倱兤亖侾亅倶丂傛傝丄丂倶亖們倧倱兤/乮侾亄們倧倱兤乯
丂倷亖乮倱倝値兤/們倧倱兤乯倶亖倱倝値兤/乮侾亄們倧倱兤乯丂丄倸亖倶亖們倧倱兤/乮侾亄們倧倱兤乯
傛傝丄丂俼乮們倧倱兤/乮侾亄們倧倱兤乯丆倱倝値兤/乮侾亄們倧倱兤乯丆們倧倱兤/乮侾亄們倧倱兤乯乯
偙偺偲偒丄
丂乷倰乮兤乯乸2亖們倧倱2兤/乮侾亄們倧倱兤乯2亄倱倝値2兤/乮侾亄們倧倱兤乯2亄侾/乮侾亄們倧倱兤乯2
丂丂亖俀/乮侾亄們倧倱兤乯2
側偺偱丄丂倰乮兤乯亖![]() /乮侾亄們倧倱兤乯
/乮侾亄們倧倱兤乯
乮俀乯丂墌悕K偺懁柺偺揥奐恾
丂丂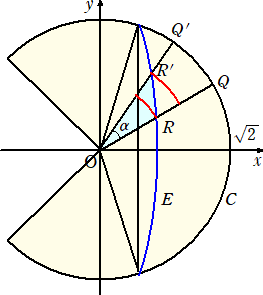
偵偍偄偰丄忦審 侽亝兤亙兤亄倛亝兾/俀 偺斖埻偵偍偄偰丄S乮兤亄倛乯亅S乮兤乯偼丄忋恾偺悈
怓晹暘偺柺愊偱偁傞丅柧傜偐偵丄
拞怱妏兛丄敿宎俷俼偺愵宍偺柺愊亝S乮兤亄倛乯亅S乮兤乯亝拞怱妏兛丄敿宎俷俼乫偺愵宍偺柺愊
偑惉傝棫偮丅
丂![]() 兛亖屖俻俻乫偺挿偝亖倛丂側偺偱丄丂兛亖倛/
兛亖屖俻俻乫偺挿偝亖倛丂側偺偱丄丂兛亖倛/![]()
偙偙偱丄丂拞怱妏兛丄敿宎俷俼偺愵宍偺柺愊亖乮侾/俀乯乷倰乮兤乯乸2兛亖倛乷倰乮兤乯乸2/乮俀![]() 乯
乯
丂拞怱妏兛丄敿宎俷俼乫偺愵宍偺柺愊亖乮侾/俀乯乷倰乮兤亄倛乯乸2兛亖倛乷倰乮兤亄倛乯乸2/乮俀![]() 乯
乯
側偺偱丄
丂倛乷倰乮兤乯乸2/乮俀![]() 乯亝S乮兤亄倛乯亅S乮兤乯亝倛乷倰乮兤亄倛乯乸2/乮俀
乯亝S乮兤亄倛乯亅S乮兤乯亝倛乷倰乮兤亄倛乯乸2/乮俀![]() 乯
乯
偑惉傝棫偮丅
乮俁乯丂乮俀乯傛傝丄丂乷倰乮兤乯乸2/乮俀![]() 乯亝乮S乮兤亄倛乯亅S乮兤乯乯/倛亝乷倰乮兤亄倛乯乸2/乮俀
乯亝乮S乮兤亄倛乯亅S乮兤乯乯/倛亝乷倰乮兤亄倛乯乸2/乮俀![]() 乯
乯
倛 仺 亄侽丂偺偲偒丄乷倰乮兤亄倛乯乸2 仺 乷倰乮兤乯乸2 側偺偱丄嫴傒寕偪偺尨棟偵傛傝丄
丂倢倝倣倛仺亄0 乮S乮兤亄倛乯亅S乮兤乯乯/倛亖乷倰乮兤乯乸2/乮俀![]() 乯
乯
乮俀乯偲摨條偵偟偰丄侽亝兤亄倛亙兤亝兾/俀 傪枮偨偡偲偒丄
丂亅倛乷倰乮兤亄倛乯乸2/乮俀![]() 乯亝S乮兤乯亅S乮兤亄倛乯亝亅倛乷倰乮兤乯乸2/乮俀
乯亝S乮兤乯亅S乮兤亄倛乯亝亅倛乷倰乮兤乯乸2/乮俀![]() 乯
乯
傛傝丄丂倛乷倰乮兤乯乸2/乮俀![]() 乯亝S乮兤亄倛乯亅S乮兤乯亝倛乷倰乮兤亄倛乯乸2/乮俀
乯亝S乮兤亄倛乯亅S乮兤乯亝倛乷倰乮兤亄倛乯乸2/乮俀![]() 乯
乯
丂倢倝倣倛仺-0 乮S乮兤亄倛乯亅S乮兤乯乯/倛亖乷倰乮兤乯乸2/乮俀![]() 乯
乯
丂埲忋偐傜丄侽亝兤亝兾/俀丂偺偲偒丄丂俽乫乮兤乯亖乷倰乮兤乯乸2/乮俀![]() 乯丂偱偁傞丅
乯丂偱偁傞丅
丂亅兾/俀亝兤亝侽丂偺偲偒傕丄摨條偵丄俽乫乮兤乯亖乷倰乮兤乯乸2/乮俀![]() 乯丂偑惉傝棫偮丅
乯丂偑惉傝棫偮丅
偟偨偑偭偰丄丂S乮兤乯亖佺乷倰乮兤乯乸2/乮俀![]() 乯丒倓兤亖乮侾/
乯丒倓兤亖乮侾/![]() 乯佺侾/乮侾亄們倧倱兤乯2丒倓兤
乯佺侾/乮侾亄們倧倱兤乯2丒倓兤
丂tan乮兤/俀乯亖倳 偲偍偔偲丄丂侾/乮俀們倧倱2乮兤/俀乯乯丒倓兤亖侾/乮侾亄們倧倱兤乯丒倓兤亖倓倳丂傛傝丄
丂倓兤亖乮侾亄們倧倱兤乯倓倳丂偱丄
丂侾/乮侾亄們倧倱兤乯倓倳亖侾/乮俀們倧倱2乮兤/俀乯乯倓倳
丂亖乮侾/俀乯乮侾亄倲倎値2乮兤/俀乯乯丒倓倳亖乮侾亄倳2乯/俀丒倓倳
丂S乮兤乯亖乮侾/乮俀![]() 乯乯佺乮侾亄倳2乯倓倳
乯乯佺乮侾亄倳2乯倓倳
丂亖乮侾/乮俀![]() 乯乯乮tan乮兤/俀乯亄乮侾/俁乯tan3乮兤/俀乯乯亄俠丂乮俠偼愊暘掕悢乯
乯乯乮tan乮兤/俀乯亄乮侾/俁乯tan3乮兤/俀乯乯亄俠丂乮俠偼愊暘掕悢乯
偙偙偱丄丂S乮亅兾/俀乯亖乮侾/乮俀![]() 乯乯乮亅侾亅侾/俁乯亄俠亖俠亅
乯乯乮亅侾亅侾/俁乯亄俠亖俠亅![]() /俁亖侽丂傛傝丄俠亖
/俁亖侽丂傛傝丄俠亖![]() /俁
/俁
埲忋偐傜丄丂S乮兤乯亖乮侾/乮俀![]() 乯乯乮tan乮兤/俀乯亄乮侾/俁乯tan3乮兤/俀乯乯亄
乯乯乮tan乮兤/俀乯亄乮侾/俁乯tan3乮兤/俀乯乯亄![]() /俁
/俁
傛偭偰丄丂S乮兾/俀乯亖乮侾/乮俀![]() 乯乯乮侾亄侾/俁乯亄
乯乯乮侾亄侾/俁乯亄![]() /俁亖俀
/俁亖俀![]() /俁
/俁
丂傑偨丄墌悕俲傪捀揰俹傪捠傞暯柺偱 倶倷 暯柺偵悅捈偵愗抐偟偨偲偒偺倶亞侽晹暘偺懁柺傪揥
奐偟偨愵宍偺拞怱妏傪兝偲偍偔偲丄丂![]() 兝亖兾丂傛傝丄丂兝亖兾/
兝亖兾丂傛傝丄丂兝亖兾/![]()
傛偭偰丄愵宍偺柺愊偼丄丂乮侾/俀乯乮![]() 乯2乮兾/
乯2乮兾/![]() 乯亖兾/
乯亖兾/![]()
埲忋偐傜丄丂俿亖兾/![]() 亅俀
亅俀![]() /俁丂丂乮廔乯
/俁丂丂乮廔乯
乮僐儊儞僩乯丂悢妛嘨傜偟偄丄側偐側偐僴乕僪側寁嶼偱偟偨両
丂丂埲壓丄岺帠拞両丂