| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俋俆 | 椷榓俇擭搙慜婜 | 丂搶杒戝妛丂 | 丂棟宯 | 丒丒丒 | 丂旝暘乮悢妛嘨乯 | 丂昗弨 |
搶杒戝妛丂慜婜棟宯乮俀侽俀係乯
戞俆栤丂倶亞俀傪枮偨偡幚悢倶偵懳偟丄俥乮倶乯亖乮侾/倶乯倢倧倗乮俀倶亅俁乯丂偲偍偔丅昁梫側傜偽丄
丂丂倢倝倣倲仺亣 (倢倧倗 倲)/倲亖侽 偱偁傞偙偲丄偍傛傃丄帺慠懳悢偺掙 e 偑 俀亙倕亙俁 傪枮偨偡偙偲傪
丂丂徹柧側偟偱梡偄偰傕傛偄丅
乮侾乯丂俥乫乮倶乯亖俧乮倶乯/乮倶2乮俀倶亅俁乯乯 偍偔偲偒丄娭悢俧乮倶乯 乮倶亞俀乯傪媮傔傛丅
乮俀乯丂乮侾乯偱媮傔偨娭悢俧乮倶乯偵懳偟丄俧乮兛乯亖侽 傪枮偨偡俀埲忋偺幚悢兛偑偨偩侾偮懚嵼
丂丂偡傞偙偲傪帵偣丅
乮俁乯丂娭悢俥乮倶乯乮倶亞俀乯 偺憹尭偲嬌尷 倢倝倣倶仺亣 俥乮倶乯 傪挷傋丄倷亖俥乮倶乯乮倶亞俀乯 偺僌儔僼偺
丂丂奣宍傪 倶倷 暯柺忋偵昤偗丅
丂丂丂偨偩偟丄乮俀乯偺兛傪梡偄偰傛偄丅僌儔僼偺墯撌偼挷傋側偔偰傛偄丅
乮係乯丂俀亝倣亙値 傪枮偨偡惍悢 倣丄値 偺慻(倣丆値)偵懳偟偰丄摍幃
丂丂(*)丂(俀倣亅俁乯値亖乮俀値亅俁乯倣
丂丂偑惉傝棫偮偲偡傞丅偙偺傛偆側慻(倣丆値)傪偡傋偰媮傔傛丅
乮夝乯乮侾乯丂俥乫乮倶乯亖乮俀倶/乮俀倶亅俁乯亅倢倧倗乮俀倶亅俁乯乯/倶2
丂亖乮俀倶亅乮俀倶亅俁乯倢倧倗乮俀倶亅俁乯乯/乮倶2乮俀倶亅俁乯乯丂傛傝丄俧乮倶乯亖俀倶亅乮俀倶亅俁乯倢倧倗乮俀倶亅俁乯
乮俀乯丂俧乫乮倶乯亖俀亅俀倢倧倗乮俀倶亅俁乯亅俀亖亅俀倢倧倗乮俀倶亅俁乯亙侽丂傛傝丄俧乮倶乯偼丄倶亞俀 偵偍偄偰
丂扨挷偵尭彮偡傞丅摿偵丄俧乮俀乯亖係亜侽丂偱丄倶 仺 亣 偺偲偒丄
丂俧乮倶乯亖乮俀倶亅俁乯乮俀倶/乮俀倶亅俁乯亅倢倧倗乮俀倶亅俁乯乯 仺 亅亣 側偺偱丄
丂俧乮兛乯亖侽 傪枮偨偡俀埲忋偺幚悢兛偑偨偩侾偮懚嵼偡傞丅
乮俁乯丂師偺憹尭昞傪摼傞丅
丂丂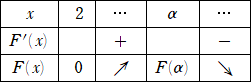
丂偨偩偟丄俧乮兛乯亖侽丂傛傝丄丂俀兛亅乮俀兛亅俁乯倢倧倗乮俀兛亅俁乯亖侽丂側偺偱丄
丂俥乮兛乯亖乮侾/兛乯倢倧倗乮俀兛亅俁乯亖俀/乮俀兛亅俁乯亝俀
丂倶 仺 亣 偺偲偒丄俥乮倶乯亖乮俀亅俁/倶乯丒乮侾/乮俀倶亅俁乯乯倢倧倗乮俀倶亅俁乯 仺 俀丒侽亖侽
丂傛偭偰丄倷亖俥乮倶乯乮倶亞俀乯 偺僌儔僼偺奣宍傪摼傞丅
丂丂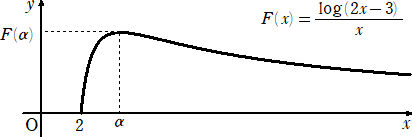
乮係乯丂(俀倣亅俁乯値亖乮俀値亅俁乯倣丂偺椉曈偺帺慠懳悢傪偲偭偰丄
丂値丒倢倧倗(俀倣亅俁乯亖倣丒倢倧倗(俀値亅俁乯丂偡側傢偪丄乮侾/倣乯倢倧倗(俀倣亅俁乯亖乮侾/値乯倢倧倗(俀値亅俁乯
偐傜丄丂俥乮倣乯亖俥乮値乯丂偲側傞 俀亝倣亙値 傪枮偨偡惍悢 倣丄値 偺慻(倣丆値)傪媮傔傟偽傛偄丅
偙偙偱丄俥乮俁乯亖乮侾/俁乯倢倧倗俁丂偱偁傞偑丄俥乮俇乯亖乮侾/俇乯倢倧倗俋亖乮侾/俁乯倢倧倗俁丂側偺偱丄
丂俥乮俁乯亖俥乮俇乯丂偑惉傝棫偮丅
丂偲偙傠偱丄俥乮係乯亖乮侾/係乯倢倧倗俆丂丄俥乮俆乯亖乮侾/俆乯倢倧倗俈丂偵偍偄偰丄
丂俆5亖俁侾俀俆丂丄俈4亖俀係侽侾丂側偺偱丄丂俆5亗俈4丂偡側傢偪丄丂俥乮係乯亗俥乮俆乯
埲忋偐傜丄俥乮倣乯亖俥乮値乯丂偲側傞 俀亝倣亙値 傪枮偨偡惍悢 倣丄値 偺慻(倣丆値)偼丄
丂乮俁丆俇乯丂偺傒偱偁傞丅丂丂乮廔乯
丂丂埲壓丄岺帠拞両丂