０９４	令和６年度前期	東北大学	理系	・・・	ベクトル（数学Ｂ）	標準

東北大学　前期理系（２０２４）

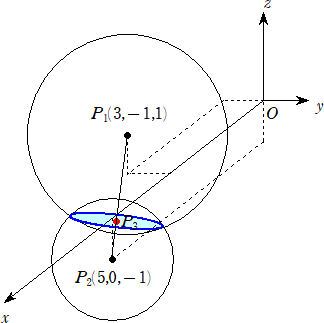
第４問　ｘｙｚ 空間において、点P₁(３，−１，１)を中心とし半径がの球面S₁と、
　　点P₂(５，０−１)を中心とし半径がの球面S₂を考える。

（１）　線分P₁P₂の長さを求めよ。
（２）　S₁とS₂が交わりをもつことを示せ。この交わりは円となる。この円をCとし、その中心を
　P₃とする。Cの半径および中心P₃の座標を求めよ。
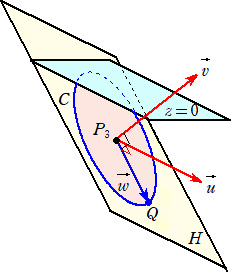
（３）　（２）の円Cに対し、Cを含む平面をHとする。ｘｙ 平面とHの両方に平行で、大きさが１の
　ベクトルをすべて求めよ。
（４）　点Qが（２）の円C上を動くとき、Qと ｘｙ 平面の距離ｄの最大値を求めよ。また、ｄ の最
　大値を与える点Qの座標を求めよ。

　　

（解）（１）　P₁P₂²＝４＋１＋４＝９　より、　P₁P₂＝３

（２）　P₁P₂＜＋　より、S₁とS₂は交わる。

　球面S₁の方程式は、　（ｘ−３）²＋（ｙ＋１）²＋（ｚ−１）²＝５　すなわち、

　　ｘ²＋ｙ²＋ｚ²−６ｘ＋２ｙ−２ｚ＋６＝０

　球面S₂の方程式は、　（ｘ−５）²＋ｙ²＋（ｚ＋１）²＝２　すなわち、

　　ｘ²＋ｙ²＋ｚ²−１０ｘ＋２ｚ＋２４＝０

　よって、Cを含む平面Hの方程式は、　４ｘ＋２ｙ−４ｚ−１８＝０　すなわち、

　　２ｘ＋ｙ−２ｚ−９＝０

　直線P₁P₂の方程式は、　（ｘ−３）/２＝ｙ＋１＝（ｚ−１）/−２　なので、

　　ｘ＝２ｔ＋３　、ｙ＝ｔ−１　、ｚ＝−２ｔ＋１

　２ｘ＋ｙ−２ｚ−９＝０　に代入して、　２（２ｔ＋３）＋ｔ−１−２（−２ｔ＋１）−９＝０　より、

　ｔ＝２/３　となるので、　Ｐ₃（１３/３，−１/３，−１/３）

　点Ｐ₁から平面Ｈに下ろした垂線の長さは、

｜２・３＋（−１）−２・１−９｜/√（４＋１＋４）＝６/３＝２

よって、円Ｃの半径 ｒ は、　ｒ₂＝５−４＝１　より、　ｒ＝１

（３）　ｘｙ 平面とHの両方に平行なベクトルを（ａ，ｂ，ｃ）とおくと、

　（ａ，ｂ，ｃ）⊥（０，０，１）　かつ　（ａ，ｂ，ｃ）⊥（２，１，−２）

から、　ｃ＝０　かつ　２ａ＋ｂ−２ｃ＝０　すなわち、　ｃ＝０　かつ　２ａ＋ｂ＝０

　ａ²＋ｂ²＋ｃ²＝１　より、　ａ²＋４ａ²＝１　よって、　ａ＝±１/

したがって、求めるベクトルは、　（１/，−２/，０）　、（−１/，２/，０）

（４）　（３）　より、ｘｙ 平面とHの両方に平行なベクトル ｕ は、

　　ｕ＝（１/，−２/，０）　、（−１/，２/，０）

　平面Hに垂直なベクトル ｖ は、ｖ＝（２，１，−２）

　ｕ 、ｖ に垂直なベクトルを ｗ＝（ｄ，ｅ，ｆ） とすると、

　ｄ−２ｅ＝０　、　２ｄ＋ｅ−２ｆ＝０　から、　ｄ＝２ｅ　、ｆ＝（５/２）ｅ

　よって、　ｗ＝（４，２，５）　としてよい。

　　

　｜ｗ｜＝３　より、ｗ方向の単位ベクトルは、±（１/（３））（４，２，５）

以上から、点Ｑの ｚ 座標は、　−１/３−/３　のとき、絶対値が最大である。

　したがって、　ｄ＝１/３＋/３＝（１＋）/３　となる。

このときの点Ｑの座標は、

（１３/３，−１/３，−１/３）−（１/（３））（４，２，５）

＝（（６５−４）/１５，−（５＋２）/１５，−（１＋）/３）

である。　　（終）


（コメント）　点Ｑの座標を求める手法が勉強になりました。空間把握がポイントですね！



　　以下、工事中！