| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俋俀 | 椷榓俇擭搙慜婜 | 丂搶杒戝妛丂 | 丂棟宯 | 丒丒丒 | 丂懳悢娭悢乮悢妛嘦乯 | 丂昗弨 |
搶杒戝妛丂慜婜棟宯乮俀侽俀係乯
戞俀栤丂埲壓偺栤偄偵摎偊傛丅
乮侾乯丂倲 傪 倲亜侾 傪枮偨偡幚悢偲偡傞丅惓偺幚悢 倶 偑俀偮偺忦審
丂乮倎乯丂倶亜侾/乮併倲亅侾乯
丂乮倐乯丂倶亞俀倢倧倗t 倶
丂傪偲傕偵枮偨偡偲偡傞丅偙偺偲偒丄晄摍幃丂倶亄侾亜俀倢倧倗t 乮倶亄侾乯丂傪帵偣丅
乮俀乯丂値亝俀倢倧倗2 値 傪枮偨偡惓偺惍悢値傪偡傋偰媮傔傛丅
乮夝乯乮侾乯丂倲亜侾 傛傝丄併倲亅侾亜侽 側偺偱丄丂倶乮併倲亅侾乯亜侾丂偡側傢偪丄丂倶併倲亜倶亄侾
丂倲 傪掙偲偡傞椉曈偺懳悢傪偲偭偰丄丂倢倧倗t 倶 亄侾/俀亜倢倧倗t 乮倶亄侾乯
偡側傢偪丄丂俀倢倧倗t 倶 亄侾亜俀倢倧倗t 乮倶亄侾乯
偙偙偱丄丂倶亞俀倢倧倗t 倶丂傛傝丄丂倶亄侾亜俀倢倧倗t 乮倶亄侾乯丂偑惉傝棫偮丅
仈丂乮俀乯傪峫嶡偡傞慜偵丄偄偔偮偐幚尡偟偰偍偙偆丅
丂値亝俀倢倧倗2 値 傪幃曄宍偟偰丄丂俀値亝値2丂偲側傞丅嵍曈偼巜悢娭悢偱丄塃曈偼俀師娭悢側偺
偱丄摉慠丄婎杮揑偵偼丄傎偲傫偳偺惓偺惍悢 値 偵懳偟偰丄俀値亜値2 偑惉傝棫偮偼偢偱偁傞丅
丂幚嵺偵丄値亖侾丂偺偲偒丄丂俀1亜侾2
丂丂値亖俀丂偺偲偒丄丂俀2亖俀2
丂丂値亖俁丂偺偲偒丄丂俀3亙俁2
丂丂値亖係丂偺偲偒丄丂俀4亖係2
丂丂値亖俆丂偺偲偒丄丂俀5亜俆2
丂丂丂丒丒丒丒丒丒丒丒丒丒丒
丂丂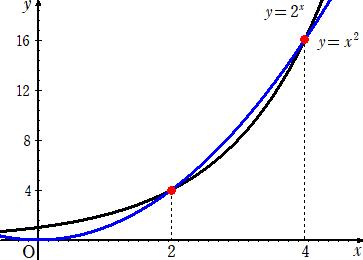
丂埲忋偐傜丄俀値亝値2丂偲側傞惓偺惍悢 値 偼丄値亖俀丄俁丄係 偱偁傞偙偲偑悇嶡偝傟傞丅
丂値亞俆 偵偍偄偰丄俀値亜値2丂偱偁傞偙偲傪帵偡偺偵丄乮侾乯傪梡偄傛丄偲偄偆偺偑僸儞僩偵側偭偰
偄傞丅
乮俀乯丂値亝俀倢倧倗2 値 傪幃曄宍偟偰丄丂俀値亝値2丂偲側傞丅
丂値亖侾丂偺偲偒丄丂俀1亜侾2丂側偺偱丄値亖侾 偼晄揔
丂値亖俀丂偺偲偒丄丂俀2亖俀2丂側偺偱丄値亖俀 偼揔
丂値亖俁丂偺偲偒丄丂俀3亙俁2丂側偺偱丄値亖俁 偼揔
丂値亖係丂偺偲偒丄丂俀4亖係2丂側偺偱丄値亖係 偼揔
丂値亖俆丂偺偲偒丄丂俀5亜俆2丂側偺偱丄値亖俆 偼晄揔
丂値亖俆丂偺偲偒丄値亜侾/乮![]() 亅侾乯亖
亅侾乯亖![]() 亄侾丂傪枮偨偟丄偐偮丄俆亞俀倢倧倗2 俆丂側偺偱丄
亄侾丂傪枮偨偟丄偐偮丄俆亞俀倢倧倗2 俆丂側偺偱丄
乮侾乯傛傝丄丂俇亜俀倢倧倗2 俇丂偡側傢偪丄丂俀6亜俇2丂偲側傞丅
丂柦戣乽値亞俆丂偵懳偟偰丄俀値亜値2 乿偑惉傝棫偮偙偲傪丄悢妛揑婣擺朄偵傛傝帵偡丅
丂値亖俆丂偺偲偒丄丂俀5亖俁俀丂丄俆2亖俀俆丂傛傝丄俀5亜俆2丂側偺偱丄値亖俆偺偲偒柦戣偼惉棫丅
丂値亖倠乮倠亞俆乯丂偺偲偒丄柦戣偑惉傝棫偮偲壖掕偡傞丅偡側傢偪丄丂俀倠亜倠2
丂偙偺偲偒丄丂倠亞俀倢倧倗2 倠丂側偺偱丄乮侾乯傛傝丄丂倠亄侾亜俀倢倧倗2 乮倠亄侾乯
丂偡側傢偪丄丂俀k+1亜乮倠亄侾乯2丂偲側傞偺偱丄柦戣偼丄値亖倠亄侾丂偺偲偒傕惉棫偡傞丅
丂埲忋偐傜丄値亞俆丂偵懳偟偰丄俀値亜値2 丂偑惉傝棫偮丅
偟偨偑偭偰丄俀値亝値2丂偲側傞惓偺惍悢 値 偼丄値亖俀丄俁丄係 偱偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂崱傑偱丄乽値亜俆丂側傜偽丄俀値亜値2 乿偼帺柧偲偡傞偙偲偑懡偐偭偨偺偱偡偑丄偒偭偪
丂丂丂丂丂丂傝帵偡偙偲偑弌棃傞傫偱偡偹両曌嫮偵側傝傑偟偨丅
丂丂埲壓丄岺帠拞両丂