| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俋侽 | 椷榓俇擭搙慜婜 | 丂杒奀摴戝妛丂 | 丂棟宯 | 丒丒丒 | 丂旝暘愊暘乮悢妛嘨乯 | 丂昗弨 |
杒奀摴戝妛丂慜婜棟宯乮俀侽俀係乯
戞俆栤丂娭悢 俥乮倶乯亖x log乮倶亄俀乯亄侾丂乮倶亜亅俀乯丂傪峫偊傞丅倷亖俥乮倶乯 偱昞偝傟傞嬋慄傪C
丂丂偲偡傞丅C偺愙慄偺偆偪孹偒偑惓偱尨揰傪捠傞傕偺傪俴偲偡傞丅偨偩偟丄log t 偼 t 偺帺慠
丂丂懳悢偱偁傞丅
乮侾乯丂捈慄俴偺曽掱幃傪媮傔傛丅
乮俀乯丂嬋慄C偼壓偵撌偱偁傞偙偲傪徹柧偣傛丅
乮俁乯丂C偲俴偍傛傃 倷 幉偱埻傑傟偨晹暘偺柺愊傪媮傔傛丅
乮夝乯乮侾乯丂倷乫亖log乮倶亄俀乯亄倶/乮倶亄俀乯丂側偺偱丄愙揰乮倲丆倲 log乮倲亄俀乯亄侾乯偵偍偗傞愙慄偺
曽掱幃偼丄丂倷亖乮log乮倲亄俀乯亄倲/乮倲亄俀乯乯乮倶亅倲乯亄倲 log乮倲亄俀乯亄侾
尨揰乮侽丆侽乯傪捠傞偺偱丄丂亅倲乮log乮倲亄俀乯亄倲/乮倲亄俀乯乯亄倲 log乮倲亄俀乯亄侾亖侽
偡側傢偪丄丂亅倲2/乮倲亄俀乯亄侾亖侽丂傛傝丄丂倲2亅倲亅俀亖侽
丂乮倲亅俀乯乮倲亄侾乯亖侽丂傛傝丄丂倲亖俀丄亅侾
倲亖俀丂偺偲偒丄倷乫亖log係亄侾/俀亜侽丂偱丄揔偡傞
倲亖亅侾丂偺偲偒丄倷乫亖亅侾亙侽丂偱丄晄揔
丂埲忋偐傜丄媮傔傞愙慄偺曽掱幃偼丄丂倷亖乮log係亄侾/俀乯倶
乮俀乯丂倷乭亖侾/乮倶亄俀乯亄乮倶亄俀亅倶乯/乮倶亄俀乯2亖侾/乮倶亄俀乯亄俀/乮倶亄俀乯2
丂倶亜亅俀丂偺偲偒丄丂倷乭亜侽丂側偺偱丄嬋慄C偼壓偵撌偱偁傞丅
乮俁乯丂
丂丂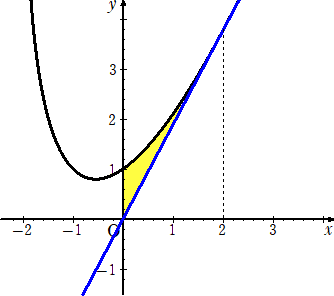
俽亖佺02 乮x log乮倶亄俀乯亄侾亅乮log係亄侾/俀乯倶乯倓倶
丂亖[倶2/俀丒log乮倶亄俀乯]02亅乮侾/俀乯佺02 倶2/乮倶亄俀乯倓倶亄[倶]02亅乮log係亄侾/俀乯[倶2/俀]02
丂亖俀log 係 亅乮侾/俀乯佺02 倶2/乮倶亄俀乯倓倶亄俀亅俀乮log係亄侾/俀乯
丂亖侾亅乮侾/俀乯佺02 倶2/乮倶亄俀乯倓倶
丂倶亄俀亖倲丂偲偍偔偲丄丂倓倶亖倓倲丂側偺偱丄
丂佺02 倶2/乮倶亄俀乯倓倶亖佺24 (倲亅俀)2/倲 倓倲
亖佺24 (倲亅係亄係/倲乯 倓倲亖[乮倲亅係乯2/俀亄係log 倲]24亖係log 係亅俀亅係log 俀亖係log 俀亅俀
丂埲忋偐傜丄丂俽亖侾亅乮侾/俀乯乮係log 俀亅俀乯亖俀亅俀log 俀丂丂乮廔乯
丂丂埲壓丄岺帠拞両丂