０８９	令和６年度前期	北海道大学	理系	・・・	ベクトル（数学Ｂ）	やや易

北海道大学　前期理系（２０２４）

第４問　△OABが、|ＯＡ|＝３、|ＡＢ|＝５、ＯＡ・ＯＢ＝１０ を満たしているとする。△OABの
　　内接円の中心を I とし、この内接円と辺OAの接点をHとする。

　　

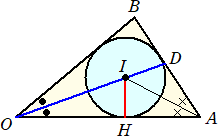
（１）　辺0Bの長さを求めよ。
（２）　ＯＩ をＯＡとＯＢを用いて表せ。
（３）　ＨＩ をＯＡとＯＢを用いて表せ。

（解）（１）　|ＯＢ−ＯＡ|²＝２５　より、　　|ＯＢ|²−２ＯＡ・ＯＢ＋|ＯＡ|²＝２５　から、

　ＯＢ²−２０＋９＝２５　なので、　ＯＢ²＝３６　よって、　OB＝６

（２）　ＯＤは∠ＡＯＢの２等分線なので、　AD ： DB＝３ ： ６＝１ ： ２

　よって、　ＯＤ＝（２/３）ＯＡ＋（１/３）ＯＢ

　さらに、ＡＤ＝５/３　で、ＡＩ は、∠ＯＡＤの２等分線なので、　ＯＩ ： ＩＤ＝３ ： ５/３＝９ ： ５

　よって、　ＯＩ＝（９/１４）ＯＤ＝（３/７）ＯＡ＋（３/１４）ＯＢ

（３）　ＯＨ＝ｘ　とおくと、　（６−ｘ）＋（３−ｘ）＝５　より、　ｘ＝２

　よって、　ＯＨ＝（２/３）ＯＡ　なので、

　ＨＩ＝ＯＩ−ＯＨ＝（−５/２１）ＯＡ＋（３/１４）ＯＢ　　（終）



　　以下、工事中！