| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俉俆 | 椷榓俇擭搙慜婜 | 丂杒奀摴戝妛丂 | 丂棟宯 | 丒丒丒 | 丂恾宍偲幃乮悢妛嘦乯 | 丂傗傗堈 |
杒奀摴戝妛丂慜婜棟宯乮俀侽俀係乯
戞侾栤丂倲 傪幚悢偲偟丄倶倷暯柺忋偺揰P(cos俀倲丆cos t) 偍傛傃 揰Q(sin t丆sin俀倲) 傪峫偊傞丅
乮侾乯丂揰P偲揰Q偑堦抳偡傞傛偆側 倲 偺抣傪偡傋偰媮傔傛丅
乮俀乯丂倲 偑 侽亙倲亙俀兾 偺斖埻偱曄壔偡傞偲偒丄揰P偺婳愓傪 倶倷 暯柺忋偵恾帵偣傛丅
丂丂偨偩偟丄倶 幉丄倷 幉偲偺嫟桳揰偑偁傞応崌偼丄偦傟傜偺嵗昗傪媮傔丄恾拞偵婰偣丅
乮夝乯乮侾乯丂戣堄傛傝丄丂cos俀倲亖sin t丂丄cos t亖sin俀倲
丂cos t亖sin俀倲丂傛傝丄丂cos t亖俀sin 倲 cos t 側偺偱丄丂cos t亖侽丂傑偨偼丄丂sin 倲亖侾/俀
丂cos t亖侽丂偺偲偒丄丂cos俀倲亖sin t丂傛傝丄丂俀cos2 t亅侾亖sin t丂偐傜丄sin t亖亅侾
丂丂丂偙偺偲偒丄倲亖俁兾/俀亄俀値兾丂乮値偼擟堄偺惍悢乯
丂sin 倲亖侾/俀丂偺偲偒丄丂cos俀倲亖sin t丂傛傝丄丂俀cos2 t亅侾亖侾/俀丂偐傜丄cos t亖亇![]() /俀
/俀
丂丂丂偙偺偲偒丄倲亖兾/俇亄俀値兾丂丄俆兾/俇亄俀値兾丂乮値偼擟堄偺惍悢乯
乮俀乯丂倶亖cos俀倲亖俀cos2 t亅侾丂丄倷亖cos t丂偲偍偔偲丄丂倶亖俀倷2亅侾
丂偙偙偱丄侽亙倲亙俀兾 傛傝丄亅侾亝倷亙侾丂側偺偱丄壓恾傪摼傞丅
丂丂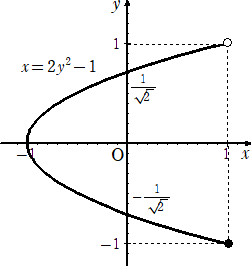 丂丂乮廔乯
丂丂乮廔乯
丂丂埲壓丄岺帠拞両丂