０８３	令和６年度前期	東京大学	理系	・・・	微分積分（数学�U）	標準

東京大学　前期理系（２０２４）

第４問　Ｆ（ｘ）＝−（/４）ｘ²＋４ とおく。０＜ｔ＜４ を満たす実数 ｔ に対し、座標平面上
　　の点(ｔ，Ｆ（ｔ））を通り、この点において放物線 ｙ＝Ｆ（ｘ） と共通の接線を持ち、ｘ 軸上に中
　　心を持つ円をＣ_ｔとする。

（１）　円Ｃ_ｔの中心の座標を(c(ｔ)，０)、半径を r(ｔ) とおく。c(ｔ) と ｛r(ｔ)｝²をｔの整式で表せ。
（２）　実数ａは ０＜ａ＜Ｆ（３） を満たすとする。円 Ｃ_ｔ が点(３，ａ)を通るような実数 ｔ は、
　　０＜ｔ＜４ の範囲にいくつあるか。

（解）（１）　題意より、下図を得る。

　　

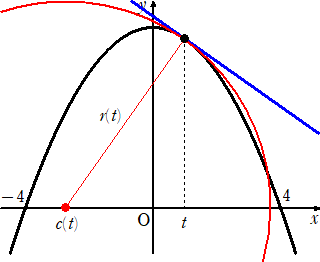
　Ｆ’（ｘ）＝−（/２）ｘ　より、接点(ｔ，Ｆ（ｔ））における法線の方程式は、

　ｙ＝（/ｔ）（ｘ−ｔ）−（/４）ｔ²＋４＝（/ｔ）ｘ−（/４）ｔ²＋３

ｙ＝０　を解いて、　ｘ＝（１/４）ｔ³−３ｔ　なので、　c(ｔ)＝（１/４）ｔ³−３ｔ

このとき、

｛r(ｔ)｝²＝（−（/４）ｔ²＋４）²＋（−（１/４）ｔ³＋４ｔ）²＝（１/１６）ｔ⁶−(１５/８)ｔ⁴＋１２ｔ²＋３２

（２）　Ｆ（３）＝（７/４）　より、　０＜ａ＜（７/４）

円Ｃ_ｔの方程式は、　（ｘ−（１/４）ｔ³＋３ｔ）²＋ｙ²＝（１/１６）ｔ⁶−(１５/８)ｔ⁴＋１２ｔ²＋３２

この円が点(３，ａ)を通るので、

　（３−（１/４）ｔ³＋３ｔ）²＋ａ²＝（１/１６）ｔ⁶−(１５/８)ｔ⁴＋１２ｔ²＋３２

すなわち、　−（３/８）ｔ⁴＋（３/２）ｔ³＋３ｔ²−１８ｔ＋２３＝ａ²

　ｙ＝−（３/８）ｔ⁴＋（３/２）ｔ³＋３ｔ²−１８ｔ＋２３　とおくと、

　ｙ’＝−（３/２）ｔ³＋（９/２）ｔ²＋６ｔ−１８

　＝−（３/２）（ｔ³−３ｔ²−４ｔ＋１２）＝−（３/２）（ｔ−２）（ｔ−３）（ｔ＋２）＝０　とおくと、

　ｔ＝２、３、−２

０＜ｔ＜４　に注意して増減表を書くと、

　　

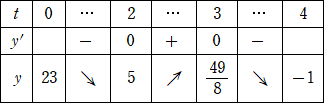
よって、ｙ＝−（３/８）ｔ⁴＋（３/２）ｔ³＋３ｔ²−１８ｔ＋２３　のグラフは、

　　

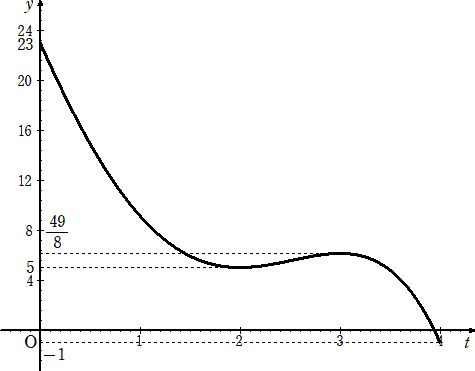
　このグラフと、直線 ｙ＝ａ² の共有点の個数を調べる。

　０＜ａ＜（７/４）　より、　０＜ａ²＜４９/８　に注意して、

　０＜ａ²＜５　すなわち、　０＜ａ＜ のとき、　１個

　ａ＝ のとき、　２個

　５＜ａ²＜４９/８　すなわち、　＜ａ＜（７/４）　のとき、　３個　　（終）



　　以下、工事中！