| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俉俀 | 椷榓俇擭搙慜婜 | 丂搶嫗戝妛丂 | 丂棟宯 | 丒丒丒 | 丂妋棪丒悢楍乮悢妛俙丒俛乯 | 丂昗弨 |
搶嫗戝妛丂慜婜棟宯乮俀侽俀係乯
戞俁栤丂嵗昗暯柺忋傪師偺婯懃乮鶣乯丄乮鶤乯偵廬偭偰侾昩偛偲偵摦偔揰P傪峫偊傞丅
乮鶣乯丂嵟弶偵丄P偼揰(俀丆侾)偵偄傞丅
乮鶤乯丂偁傞帪崗偱P偑揰(倎丆倐)偵偄傞偲偒丄偦偺侾昩屻偵偼P偼
丂丒妋棪侾/俁偱 倶 幉偵娭偟偰(倎丆倐)偲懳徧側揰
丂丒妋棪侾/俁偱 倷 幉偵娭偟偰(倎丆倐)偲懳徧側揰
丂丒妋棪侾/俇偱捈慄 倷亖倶 偵娭偟偰(倎丆倐)偲懳徧側揰
丂丒妋棪侾/俇偱捈慄 倷亖亅倶 偵娭偟偰(倎丆倐)偲懳徧側揰
偵偄傞丅
丂埲壓偺栤偄偵摎偊傛丅偨偩偟丄乮侾乯偵偮偄偰偼丄寢榑偺傒傪彂偗傁傛偄丅
乮侾乯丂P偑偲傝偆傞揰偺嵗昗傪偡傋偰媮傔傛丅
乮俀乯丂値傪惓偺惍悢偲偡傞丅嵟弶偐傜値昩屻偵P偑揰(俀丆侾)偵偄傞妋棪偲丄嵟弶偐傜値昩屻偵
丂丂P偑揰(亅俀丆亅侾)偵偄傞妋棪偼摍偟偄偙偲傪帵偣丅
乮俁乯丂値傪惓偺惍悢偲偡傞丅嵟弶偐傜値昩屻偵P偑揰(俀丆侾)偵偄傞妋棪傪媮傔傛丅
仈摦揰俹偑揰(俀丆侾)偵偄傞偲偒偺堏摦偺忬嫷傪恾帵偟偰傒偨丅
丂丂
乮夝乯丂壓恾傛傝丄P偑偲傝偆傞揰偺嵗昗偼丄
(俀丆侾)丄(侾丆俀)丄(亅侾丆俀)丄(亅俀丆侾)丄(亅俀丆亅侾)丄(亅侾丆亅俀)丄(侾丆亅俀)丄(俀丆亅侾)丂偺俉揰
丂丂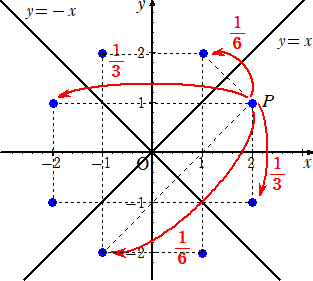
乮俀乯丂俹偺堏摦忬嫷傪惛嵏偡傞偲丄俹偺侾昩屻偵偄傞偺偼丄乷俛1丆俛2丆俛3丆俛4}偺壗傟偐偱丄
偝傜偵偦偺侾昩屻偵偄傞偺偼丄乷俙1丆俙2丆俙3丆俙4}偺壗傟偐偱丄埲屻丄乷俛1丆俛2丆俛3丆俛4}丄
乷俙1丆俙2丆俙3丆俙4}偵俹偑偄傞忬嫷偑岎屳偵尰傟傞丅
丂丂
丂嵟弶偐傜値昩屻偵P偑揰(俀丆侾)偵偄傞偨傔偵偼丄
丂値亅侾昩屻偵丄俛2丄俛4偐傜妋棪侾/俁偱俙1偵堏傝丄俛1丄俛3偐傜妋棪侾/俇偱俙1偵堏傞
丂嵟弶偐傜値昩屻偵P偑揰(亅俀丆亅侾)偵偄傞偨傔偵偼丄
丂値亅侾昩屻偵丄俛2丄俛4偐傜妋棪侾/俁偱俙1偵堏傝丄俛1丄俛3偐傜妋棪侾/俇偱俙3偵堏傞
傛偭偰丄嵟弶偐傜値昩屻偵P偑揰(俀丆侾)偵偄傞妋棪偲丄嵟弶偐傜値昩屻偵P偑揰(亅俀丆亅侾)偵
偄傞妋棪偼摍偟偄丅
乮俁乯丂嵟弶偐傜値昩屻偵丄俙1丆俙3偵偄傞妋棪傪倎値丂丄俛1丄俛3偵偄傞妋棪傪倐値
丂俙2丆俙4偵偄傞妋棪傪們値丂丄俛2丆俛4偵偄傞妋棪傪倓値
偲偍偔偲丄丂倎値+1亖乮侾/俁乯倐値亄乮俀/俁乯倓値丂丄倐値+1亖乮侾/俁乯倎値亄乮俀/俁乯們値
丂們値+1亖乮侾/俁乯倓値亄乮俀/俁乯倐値丂丄倓値+1亖乮侾/俁乯們値亄乮俀/俁乯倎値
偨偩偟丄弶婜忦審偼丄丂倎0亖侾丂丄倐0亖侽丂丄們0亖侽丂丄倓0亖侽丂側偺偱丄
丂倎1亖侽丂丄倐1亖侾/俁丂丄們1亖侽丂丄倓1亖俀/俁
偙偺偲偒丄丂倎値+1亄們値+1亖倐値亄倓値丂丄倐値+1亄倓値+1亖倎値亄們値丂偐傜丄
丂倎値+1亄們値+1亖倎値-1亄們値-1丂側偺偱丄丂倎値亄們値亖倎値-2亄們値-2亖丒丒丒
傛偭偰丄
丂値偑嬼悢偺偲偒丄丂倎値亄們値亖倎0亄們0亖侾丂丄値偑婏悢偺偲偒丄丂倎値亄們値亖倎1亄們1亖侽
摨條偵偟偰丄丂倎値+1亅們値+1亖亅乮侾/俁乯乮倐値亅倓値乯丂丄倐値+1亅倓値+1亖亅乮侾/俁乯乮倎値亅們値乯
偐傜丄丂倎値+1亅們値+1亖乮侾/俋乯乮倎値-1亅們値-1乯丂側偺偱丄丂倎値亅們値亖乮侾/俋乯乮倎値-2亅們値-2乯
傛偭偰丄
丂値偑嬼悢偺偲偒丄倎値亅們値亖乮侾/俁乯値乮倎0亅們0乯亖乮侾/俁乯値丂丄値偑婏悢偺偲偒丄丂倎値亅們値亖侽
埲忋偐傜丄値偑嬼悢偺偲偒丄丂倎値亖乮侾亄乮侾/俁乯値乯/俀丂丄値偑婏悢偺偲偒丄丂倎値亖侽丂側偺偱丄
媮傔傞妋棪偼丄乮俀乯傛傝丄
値偑嬼悢偺偲偒丄丂乮侾/俀乯倎値亖乮侾亄乮侾/俁乯値乯/係丂丄値偑婏悢偺偲偒丄丂乮侾/俀乯倎値亖侽丂丂乮廔乯
乮僐儊儞僩乯丂妋棪偲慟壔幃丄廫暘妝偟傔傑偟偨両
丂丂埲壓丄岺帠拞両丂