| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俉侾 | 椷榓俇擭搙屻婜 | 丂杒奀摴戝妛丂 | 丂棟宯 | 丒丒丒 | 丂夞揮懱偺懱愊乮悢妛嘨乯 | 丂昗弨 |
杒奀摴戝妛丂屻婜棟宯乮俀侽俀係乯
戞係栤丂侽亙倲亙侾 偲偟丄倷亖倱倝値 倶 乮侽亝倶亝倲乯 偱掕傑傞嬋慄傪C偲偡傞丅揰P(倲丆倱倝値 倲) 傪捠傝
丂丂倷幉偲暯峴側捈慄傪俴1丄P傪捠傝 倶 幉偲暯峴側捈慄傪俴2 偲偡傞丅
丂丂俴1丄x 幉丄C偱埻傑傟傞恾宍偑 倶 幉偺廃傝偵侾夞揮偟偰偱偒傞棫懱偺懱愊傪 V(倲) 偲偡傞丅
丂丂俴2丄倷 幉丄C偱埻傑傟傞恾宍偑 倷 幉偺廃傝偵侾夞揮偟偰偱偒傞棫懱偺懱愊傪 W(倲) 偲偡傞丅
丂丂丂偙偺偲偒丄師偺栤偵摎偊傛丅偨偩偟丄昁梫側傜偽丄
丂丂倢倝倣t仺0 乮們倧倱 倲 /倲2亅倱倝値 倲 /倲3乯亖亅侾/俁丂傪梡偄偰傕傛偄丅
乮侾乯丂V(倲) 傪媮傔傛丅
乮俀乯丂W(t) 傪媮傔傛丅
乮俁乯丂嬌尷丂倢倝倣t仺+0 W(t)/乮兾倲2倱倝値 倲乯 傪媮傔傛丅
丂丂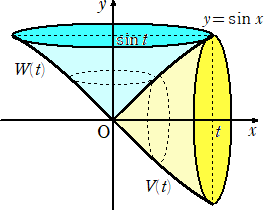
仈摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偐傜栤戣傪偛採嫙偄偨偩偒傑偟偨丅
丂乮椷榓俇擭俁寧俀係擔晅偗乯
乮夝乯乮侾乯丂戣堄傛傝丄
丂![]()
乮俀乯丂戣堄傛傝丄
丂![]()
丂晹暘愊暘傪寁嶼偟偰丄
丂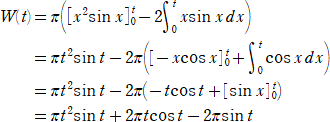
乮俁乯丂倲 仺 亄侽丂偺偲偒丄倱倝値 倲 /倲 仺 侾丂偵拲堄偟偰丄
丂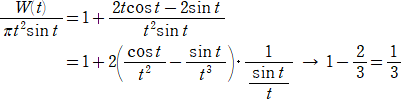 丂丂乮廔乯
丂丂乮廔乯
乮僐儊儞僩乯丂揟宆揑側夞揮懱偺懱愊寁嶼偱偟偨丅
僸儞僩偺丂倢倝倣t仺0 乮們倧倱 倲 /倲2亅倱倝値 倲 /倲3乯亖亅侾/俁丂偼丄儘僺僞儖偺掕棟偐傜柧傜偐偱偟傚偆丅
丂丂埲壓丄岺帠拞両丂