| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俈俋 | 椷榓俇擭搙慜婜 | 丂搶嫗戝妛丂 | 丂棟宯 | 丒丒丒 | 丂俀師嬋慄乮悢妛嘨乯 | 丂傗傗堈 |
搶嫗戝妛丂慜婜棟宯乮俀侽俀係乯
戞侾栤丂嵗昗嬻娫撪偺揰A(侽丆亅侾丆侾)傪偲傞丅xy 暯柺忋偺揰P偑師偺忦審乮鶣乯丄乮鶤乯丄乮鶥乯
丂丂傪偡傋偰枮偨偡偲偡傞丅
乮鶣乯丂P偼尨揰俷偲堎側傞丅
乮鶤乯丂佢俙俷俹亞俀兾/俁
乮鶥乯丂佢俷俙俹亝兾/俇
丂偙偺偲偒丄P偑偲傝偆傞斖埻傪 xy 暯柺忋偵恾帵偣傛丅
仈戣堄傪棟夝偡傞偨傔偵丄忋婰偺忦審傪枮偨偡揰俹偺偄偔偮偐傪嶌夋偟偰傒偨丅
丂丂
丂佢俙俷俹亖俁兾/係亞俀兾/俁丂偺傕偲偱丄佢俷俙俹乫亖兾/侾俀亝兾/俇丂偲側傞揰俹乫
丂佢俙俷俹亖俁兾/係亞俀兾/俁丂偺傕偲偱丄佢俷俙俹乭亖兾/俇丂偲側傞揰俹乭
丂媮傔傞揰俹偼丄俹乫傗俹乭偺廃曈偩傠偆偲悇應偝傟傞丅
乮夝乯丂戣堄傛傝丄俹乮倶丆倷丆侽乯偲偟偰丄
丂丂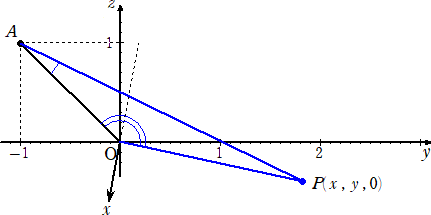
丂俷俙亖乮侽丆亅侾丆侾乯丄俷俹亖乮倶丆倷丆侽乯丂偲偍偔丅戣堄傛傝丄
丂俷俙偲俷俹偺側偡妏偑俀兾/俁埲忋側偺偱丄丂亅倷/乮![]() 併乮倶2亄倷2乯乯亝亅侾/俀
併乮倶2亄倷2乯乯亝亅侾/俀
丂偡側傢偪丄丂![]() 倷亞併乮倶2亄倷2乯丂傛傝丄丂倷亞侽丂偐偮丂倷2亞倶2
倷亞併乮倶2亄倷2乯丂傛傝丄丂倷亞侽丂偐偮丂倷2亞倶2
丂偙偙偱丄倷2亅倶2亖乮倷亄倶乯乮倷亅倶乯亞侽丂傛傝丄
丂丂乮倷亄倶亞侽丂偐偮丂倷亅倶亞侽乯丂傑偨偼丄丂乮倷亄倶亝侽丂偐偮丂倷亅倶亝侽乯
埲忋偐傜丄
丂丂
丂摨條偵偟偰丄俙俷亖乮侽丆侾丆亅侾乯 偲 俙俹亖乮倶丆倷亄侾丆亅侾乯 偺側偡妏偑兾/俇埲壓側偺偱丄丂
丂乮倷亄俀乯/乮![]() 併乮倶2亄乮倷亄侾乯2亄侾乯乯亞
併乮倶2亄乮倷亄侾乯2亄侾乯乯亞![]() /俀
/俀
丂偡側傢偪丄丂![]() 乮倷亄俀乯亞
乮倷亄俀乯亞![]() 併乮倶2亄乮倷亄侾乯2亄侾乯丂傛傝丄
併乮倶2亄乮倷亄侾乯2亄侾乯丂傛傝丄
丂倷亄俀亞侽丂偐偮丂俀乮倷亄俀乯2亞俁乮倶2亄乮倷亄侾乯2亄侾乯
丂偙偙偱丄俀乮倷亄俀乯2亞俁乮倶2亄乮倷亄侾乯2亄侾乯丂傛傝丄丂俁倶2亄倷2亅俀倷亅俀亝侽丂側偺偱丄
丂丂倶2亄乮倷亅侾乯2/俁亝侾
埲忋偐傜丄
丂丂
丂偟偨偑偭偰丄媮傔傞俹偺斖埻偼丄壓恾偺捠傝偲側傞丅
丂丂
丂偨偩偟丄尨揰乮侽丆侽乯偼彍偔丅
乮僐儊儞僩乯丂倷 幉忋偺揰偑丄朻摢偱寁嶼偟偨晹暘偱偡偹両
丂丂埲壓丄岺帠拞両丂