| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俈俇 | 椷榓俇擭搙慜婜 | 丂嫗搒戝妛丂 | 丂棟宯 | 丒丒丒 | 丂旝暘愊暘乮悢妛嘨乯 | 丂昗弨 |
嫗搒戝妛丂慜婜棟宯乮俀侽俀係乯
戞俆栤丂倎 偼丄倎亞侾 傪枮偨偡掕悢偲偡傞丅嵗昗暯柺忋偱丄師偺係偮偺晄摍幃偑昞偡椞堟傪
丂丂俢a 偲偡傞丅
丂倶亞侽丂丄乮ex亅e-x乯/俀亝倷丂丄倷亝乮ex亄e-x乯/俀丂丄倷亝倎
丂師偺栤偄偵摎偊傛丅
乮侾乯丂俢a 偺柺愊 俽a 傪媮傔傛丅
乮俀乯丂lima仺亣 俽a 傪媮傔傛.
乮夝乯丂乮ex亄e-x乯/俀亖倎 傛傝丄丂倶亖倢倧倗乮倎亄併乮倎2亅侾乯乯乮亖倐 偲偍偔丅乯
丂乮ex亅e-x乯/俀亖倎 傛傝丄丂倶亖倢倧倗乮倎亄併乮倎2亄侾乯乯乮亖們 偲偍偔丅乯
偙偺偲偒丄係偮偺晄摍幃偑昞偡椞堟 俢a 偼丄壓恾偺捠傝丅
丂丂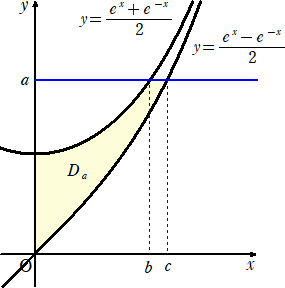
乮侾乯丂媮傔傞柺愊 俽a 偼丄
丂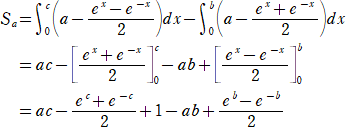
偙偙偱丄丂倕倐亖倎亄併乮倎2亅侾乯丂丄倕-倐亖倎亅併乮倎2亅侾乯
丂倕們亖倎亄併乮倎2亄侾乯丂丄倕-們亖併乮倎2亄侾乯亅倎丂側偺偱丄
俽a亖倎們亅併乮倎2亄侾乯亄侾亅倎倐亄併乮倎2亅侾乯
亖侾亄倎乮倢倧倗乮倎亄併乮倎2亄侾乯乯亅倢倧倗乮倎亄併乮倎2亅侾乯乯乯亄併乮倎2亅侾乯亅併乮倎2亄侾乯
亖侾亄倎丒倢倧倗乷乮倎亄併乮倎2亄侾乯乯/乮倎亄併乮倎2亅侾乯乯乸亄併乮倎2亅侾乯亅併乮倎2亄侾乯
乮俀乯丂乮侾乯傛傝丄倎 仺亣 偺偲偒丄
丂乮倎亄併乮倎2亄侾乯乯/乮倎亄併乮倎2亅侾乯乯
亖乮侾亄併乮侾亄侾/倎2乯乯/乮侾亄併乮侾亅侾/倎2乯乯 仺 侾
丂併乮倎2亅侾乯亅併乮倎2亄侾乯
亖亅俀/乮併乮倎2亅侾乯亄併乮倎2亄侾乯乯 仺 侽
傛偭偰丄丂俽a 仺 侾亄倎丒倢倧倗侾亄侽亖侾丂丂乮廔乯
丂丂埲壓丄岺帠拞両丂