| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俈侾 | 椷榓俇擭搙慜婜 | 丂搶嫗戝妛丂 | 丂暥宯 | 丒丒丒 | 丂嶰妏娭悢乮悢妛嘦乯 | 丂昗弨 |
搶嫗戝妛丂慜婜暥宯乮俀侽俀係乯
戞俁栤丂嵗昗暯柺忋偵俀揰俷(侽丆侽)丄A(侽丆侾)傪偲傞丅倶 幉忋偺俀揰P(倫丆侽)丄Q(倯丆侽)偑丄師
丂丂偺忦審乮鶣乯丄乮鶤乯傪偲傕偵枮偨偡偲偡傞丅
乮鶣乯丂侽亙倫亙侾丂偐偮丂倫亙倯
乮鶤乯丂慄暘俙俹偺拞揰傪俵偲偡傞偲偒丄佢俷俙俹亖佢俹俵俻
乮侾乯丂倯 傪 倫 傪梡偄偰昞偣丅
乮俀乯丂倯亖侾/俁 偲側傞倫偺抣傪媮傔傛丅
乮俁乯丂仮俷俙俹偺柺愊傪S丄仮俹俵俻偺柺愊傪俿偲偡傞丅俽亜俿 偲側傞 倫 偺斖埻傪媮傔傛丅
乮夝乯丂戣堄傛傝丄壓恾傪摼傞丅
丂丂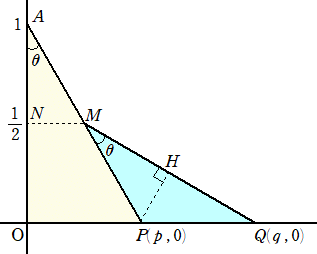
乮侾乯丂忋恾傛傝丄丂倫亖倲倎値兤丂偼柧傜偐丅
丂佢俷俹俙亖佢俵俹俫亖兾/俀亅兤丂側偺偱丄丂佢俻俹俫亖兾亅乮兾/俀亅兤乯亊俀亖俀兤
丂俵俫亖侾/俀丂側偺偱丄俹俫亖乮侾/俀乯倲倎値兤
傛偭偰丄俹俻亖俹俫/們倧倱俀兤亖乮侾/俀乯倲倎値兤/們倧倱俀兤亖倲倎値兤/乮俀們倧倱俀兤乯
偙偙偱丄丂們倧倱俀兤亖俀們倧倱2兤亅侾亖俀/乮倫2亄侾乯亅侾亖乮侾亅倫2乯/乮倫2亄侾乯丂側偺偱丄
丂倯亅倫亖倫乮倫2亄侾乯/乮俀乮侾亅倫2乯乯丂傛傝丄丂倯亖乮俁倫亅倫3乯/乮俀乮侾亅倫2乯乯
乮俀乯丂倯亖侾/俁 偺偲偒丄丂乮俁倫亅倫3乯/乮俀乮侾亅倫2乯乯亖侾/俁
丂偡側傢偪丄丂俁倫3亅俀倫2亅俋倫亄俀亖侽丂傛傝丄丂乮倫亅俀乯乮俁倫2亄係倫亅侾乯亖侽
丂偙傟傪夝偄偰丄丂倫亖俀丄乮亅俀亇![]() 乯/俁
乯/俁
丂偙偙偱丄侽亙倫亙侾丂側偺偱丄丂倫亖乮亅俀亄![]() 乯/俁
乯/俁
乮俁乯丂俽亖乮侾/俀乯倲倎値兤
丂傑偨丄俵俻亖俵俫亄俫俻亖侾/俀亄乮侾/俀乯倲倎値兤倲倎値俀兤丂側偺偱丄
丂俿亖乮侾/俀乯丒乮侾/俀乯倲倎値兤丒乮侾/俀亄乮侾/俀乯倲倎値兤倲倎値俀兤乯
丂亖乮侾/俉乯倲倎値兤乮侾亄倲倎値兤倲倎値俀兤乯
俽亜俿丂傛傝丄丂乮侾/俀乯倲倎値兤亜乮侾/俉乯倲倎値兤乮侾亄倲倎値兤倲倎値俀兤乯
偡側傢偪丄丂俁亜倲倎値兤倲倎値俀兤亖俀倫2/乮侾亅倫2乯丂偐傜丄丂俆倫2亙俁
傛偭偰丄丂侽亙倫亙![]() /俆丂丂乮廔乯
/俆丂丂乮廔乯
乮僐儊儞僩乯丂庤崰側嶰妏娭悢偺栤戣偱偡偹丅
丂丂埲壓丄岺帠拞両丂