| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俇俋 | 椷榓俇擭搙慜婜 | 丂嫗搒戝妛丂 | 丂棟宯 | 丒丒丒 | 丂暋慺悢暯柺乮悢妛嘨乯 | 丂昗弨 |
嫗搒戝妛丂慜婜棟宯乮俀侽俀係乯
戞俀栤丂|x|亝俀 傪枮偨偡暋慺悢 倶 偲丄|倷亅(俉亄俇倝)|亖俁 傪枮偨偡暋慺悢 倷 偵懳偟偰丄
丂倸亖乮倶亄倷乯/俀 偲偡傞丅偙偺傛偆側暋慺悢 倸 偑暋慺悢暯柺偵偍偄偰摦偔椞堟傪恾帵偟丄偦
丂偺柺愊傪媮傔傛丅
乮夝乯丂|x|亝俀 傛傝丄倶亖倰倕倝兤丂乮侽亝倰亝俀乯丂偲偍偗傞丅
丂|倷亅(俉亄俇倝)|亖俁 傛傝丄倷亖俉亄俇倝亄俁倕倝冇丂偲偍偗傞丅
偙偺偲偒丄倸亖乮倶亄倷乯/俀亖係亄俁倝亄乮倰/俀乯倕倝兤亄乮俁/俀乯倕倝冇丂偲彂偗傞丅
乮倰/俀乯倕倝兤 偼丄尨揰拞怱偱敿宎侾偺墌偺撪晹偍傛傃廃傪昞偡丅
係亄俁倝亄乮倰/俀乯倕倝兤 偼丄係亄俁倝 拞怱偱敿宎侾偺墌偺撪晹偍傛傃廃傪昞偡丅
乮俁/俀乯倕倝冇 偼丄尨揰拞怱偱敿宎俁/俀偺廃傪昞偡丅
偟偨偑偭偰丄係亄俁倝亄乮倰/俀乯倕倝兤亄乮俁/俀乯倕倝冇丂偼丄
丂係亄俁倝 拞怱偱敿宎侾偺墌偺撪晹偍傛傃廃忋偺揰傪拞怱偲偟偰敿宎俁/俀偺廃傪昞偡丅
傛偭偰丄媮傔傞椞堟偼丄壓恾偺墌娐晹暘乮墿怓晹暘乯偱偁傞丅
丂丂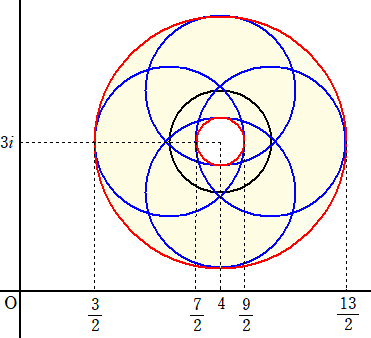
丂傛偭偰丄媮傔傞柺愊偼丄丂兾乮俆/俀乯2亅兾乮侾/俀乯2亖俇兾丂丂乮廔乯
丂丂埲壓丄岺帠拞両丂