０６８	令和６年度前期	京都大学	文系	・・・	空間図形（数学Ｉ）	標準

京都大学　前期文系（２０２４）

第１問　四面体OABCが次を満たすとする。

　ＯＡ＝OB＝OC＝１、∠COA＝∠COB＝∠ACB、∠AOB＝９０°

　　

　このとき、四面体OABCの体積を求めよ。

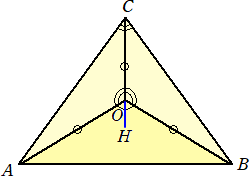
（解）　頂点Ｏから平面ＡＢＣに下した垂線の足をＨとおく。

　題意より、Ｈは△ＡＢＣの外心である。ＡＢ＝ なので、正弦定理より、

　２ＣＨ＝/ｓｉｎ∠ＡＣＢ　すなわち、　ＣＨ＝１/（ｓｉｎ∠ＡＣＢ）

∠COA＝∠COB＝∠ACB＝２θ　とおくと、　ＣＨ＝１/（ｓｉｎ２θ）

また、ＡＣ＝ＢＣ＝２ｓｉｎθ　で、　ｓｉｎθ＝（１/）/（２ｓｉｎθ）　より、　

　ｓｉｎ²θ＝１/（２）＝/４

このとき、　ｃｏｓ²θ＝１−/４＝（４−）/４　なので、

　ｓｉｎ²２θ＝４ｓｉｎ²θｃｏｓ²θ＝（４−）/４＝（２−１）/２

より、　ｓｉｎ２θ＝√（２−１）　なので、　ＣＨ＝１/√（２−１）

よって、ＯＨ²＝１−１/（２−１）＝（２−２）/（２−１）　なので、

　ＯＨ＝√（２−２）/√（２−１）

ここで、

△ＡＢＣ＝（１/２）ＡＣ・ＢＣ・ｓｉｎ２θ＝２ｓｉｎ²θｓｉｎ２θ

　＝（/２）・√（２−１）/＝√（２−１）/２

なので、求める四面体OABCの体積は、

　√（２−１）/２・√（２−２）/√（２−１）・（１/３）＝（１/６）・√（２−２）　　（終）


（コメント）　数字の汚さに、本番の試験場では自信が持てないですね！


　カルピスさんからのコメントです。（令和６年３月１３日付け）

　「数字の汚さに本番の試験では自信が持てない」とのことですが、私も答えの数字が汚い
と、間違っているのではと、相当不安になります。精神面の強さも試されているよーな。。。



　　以下、工事中！